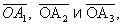 вращающихся с постоянной угловой скоростью w, причём
вращающихся с постоянной угловой скоростью w, причём 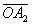 и
и 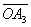 повёрнуты относительно
повёрнуты относительно  на углы a и b. Длина векторов соответствует амплитудам колебаний:
на углы a и b. Длина векторов соответствует амплитудам колебаний:Векторная диаграмма, графическое изображение значений периодически изменяющихся величин и соотношений между ними при помощи направленных отрезков — векторов.
В. д. широко применяются в электротехнике, акустике, оптике и т. п.
a1 = B1sinwt, f2 = B2sin(a + wt),
f3 = B3sin(b + wt),
могут быть представлены графически (рис.) в виде проекции на ось Оу векторов
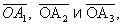 вращающихся с постоянной угловой скоростью w, причём
вращающихся с постоянной угловой скоростью w, причём 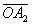 и
и 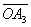 повёрнуты относительно
повёрнуты относительно  на углы a и b. Длина векторов соответствует амплитудам колебаний:
на углы a и b. Длина векторов соответствует амплитудам колебаний:

Сумма или разность двух и более колебаний на В. д. обозначается как геометрическая сумма или разность векторов составляющих колебаний, полученная по правилу параллелограмма, а мгновенное значение искомой величины определяется проекцией вектора суммы на ось Оу.
Например, требуется найти сумму F колебаний f1 с амплитудой  и f2 амплитудой
и f2 амплитудой  . При геометрическом сложении векторов
. При геометрическом сложении векторов  и
и  по В. д. находим, что амплитуда суммарного колебания F равна длине вектора
по В. д. находим, что амплитуда суммарного колебания F равна длине вектора  и опережает по фазе колебание f1 на угол j.
и опережает по фазе колебание f1 на угол j.

Рис. к ст. Векторная диаграмма.