Векторное пространство, математическое понятие, обобщающее понятие совокупности всех (свободных) векторов обычного трёхмерного пространства.

  Определение В. п. Для векторов трёхмерного пространства указаны правила сложения векторов и умножения их на действительные числа (см. Векторное исчисление). В применении к любым векторам х, у, z и любым числам a, b эти правила удовлетворяют следующим условиям (условия А):

  1) х + у = у + х (перестановочность сложения);

  2) (х + у) + z = x + (y + z) (ассоциативность сложения);

  3) имеется нулевой вектор 0 (или нуль-вектор), удовлетворяющий условию x + 0 = x: для любого вектора x;

  4) для любого вектора х существует противоположный ему вектор у такой, что х + у = 0,

  5) 1 · х = х,

  6) a(bx) = (ab) х (ассоциативность умножения);

  7) (a + b) х = aх + bх (распределительное свойство относительно числового множителя);

  8) a(х + у) = aх + aу (распределительное свойство относительно векторного множителя).

  Векторным (или линейным) пространством называется множество R, состоящее из элементов любой природы (называемых векторами), в котором определены операции сложения элементов и умножения элементов на действительные числа, удовлетворяющие условиям А (условия 1—3 выражают, что операция сложения, определённая в В. п., превращает его в коммутативную группу). Выражение

  a₁e₁ + a₂e₂ + … + a_ne_n   (1)

  называется линейной комбинацией векторов e₁, e₂,..., e_n с коэффициентами a₁, a₂,..., a_n. Линейная комбинация (1) называется нетривиальной, если хотя бы один из коэффициентов a₁, a₂,..., a_n отличен от нуля. Векторы e₁, e₂,..., e_n называются линейно зависимыми, если существует нетривиальная комбинация (1), представляющая собой нулевой вектор. В противном случае (то есть если только тривиальная комбинация векторов e₁, e₂,..., e_n равна нулевому вектору) векторы e₁, e₂,..., e_n называется линейно независимыми.

  Векторы (свободные) трёхмерного пространства удовлетворяют следующему условию (условие В): существуют три линейно независимых вектора; любые четыре вектора линейно зависимы (любые три ненулевых вектора, не лежащие в одной плоскости, являются линейно независимыми).

  В. п. называется n-мepным (или имеет «размерность n»), если в нём существуют n линейно независимых элементов e₁, e₂,..., e_n, а любые n + 1 элементов линейно зависимы (обобщённое условие В). В. п. называются бесконечномерным, если в нём для любого натурального n существует n линейно независимых векторов. Любые n линейно независимых векторов n-мepного В. п. образуют базис этого пространства. Если e₁, e₂,..., e_n — базис В. п., то любой вектор х этого пространства может быть представлен единственным образом в виде линейной комбинации базисных векторов:

  x = a₁e₁ + a₂e₂ +... + a_ne_n.

  При этом числа a₁, a_2,..., a_n называются координатами вектора х в данном базисе.

  Примеры В. п. Множество всех векторов трёхмерного пространства образует, очевидно, В. п. Более сложным примером может служить так называемое n-мерное арифметическое пространство. Векторами этого пространства являются упорядоченные системы из n действительных чисел: l ₁, l ₂,..., l _n. Сумма двух векторов и произведение на число определяются соотношениями:

  (l₁, l₂, …, l_n) + (m₁, m₂, …, m_n) = (l₁ + m₁, l₂ + m₂, …, l_n + m_n);

  a(l₁, l₂, …, l_n) = (al₁, al₂, …, al_n).

  Базисом в этом пространстве может служить, например, следующая система из n векторов e₁ = (1, 0,..., 0), e₂ = (0, 1,..., 0),..., e_n = (0, 0,..., 1).

  Множество R всех многочленов a₀ + a₁u + … + a_nuⁿ (любых степеней n) от одного переменного с действительными коэффициентами a₀, a₁,..., a_n с обычными алгебраическими правилами сложения многочленов и умножения многочленов на действительные числа образует В. п. Многочлены 1, u, u²,..., uⁿ (при любом n) линейно независимы в R, поэтому R — бесконечномерное В. п.

  Многочлены степени не выше n образуют В. п. размерности n + 1; его базисом могут служить многочлены 1, u, u²,..., uⁿ.

  Подпространства В. п. В. п. R' называется подпространством R, если R' Í R (то есть каждый вектор пространства R' есть и вектор пространства R) и если для каждого вектора v Î r' и для каждых двух векторов v₁ и v₂ (v₁, v₂ Î R') вектор lv (при любом l) и вектор v₁ + v₂ один и тот же независимо от того, рассматриваются ли векторы v, v₁, v₂ как элементы пространства R' или R. Линейной оболочкой векторов x₁, x₂,... x_p называется множество всевозможных линейных комбинаций этих векторов, то есть векторов вида a₁x₁ + a₂x₂ + … + a_px_p. В трёхмерном пространстве линейной оболочкой одного ненулевого вектора x₁ будет, очевидно, совокупность всех векторов, лежащих на прямой, определяемой вектором x₁. Линейной оболочкой двух не лежащих на одной прямой векторов x₁ и x₂ будет совокупность всех векторов, расположенных в плоскости, которую определяют векторы x₁ и x₂. В общем случае произвольного В. п. R линейная оболочка векторов x₁, x₂,..., x_p этого пространства представляет собой подпространство пространства R размерности р. В n-мерном В. п. существуют подпространства всех размерностей, меньших р. Всякое конечномерное (данной размерности k) подпространство R' В. п. R есть линейная оболочка любых k линейно независимых векторов, лежащих в R'. Пространство, состоящее из всех многочленов степени £ n (линейная оболочка многочленов 1, u, u²,..., uⁿ), есть (n + 1)-мepное подпространство пространства R всех многочленов.

  Евклидовы пространства. Для развития геометрических методов в теории В. п. нужно указать пути обобщения таких понятий, как длина вектора, угол между векторами и т.п. Один из возможных путей заключается в том, что любым двум векторам х и у из R ставится в соответствие число, обозначаемое (х, у) и называемое скалярным произведением векторов х и у. При этом требуется, чтобы выполнялись следующие аксиомы скалярного произведения:

  1) (х, у) = (у, х) (перестановочность);

  2) (x₁ + x₂, y) = (x₁, y) + (x₂, y) (распределительное свойство);

  3) (ax, у) = a(х, у),

  4) (х, х) ³ 0 для любого х, причем (х, х) = 0 только для х = 0.

  Обычное скалярное произведение в трёхмерном пространстве этим аксиомам удовлетворяет. В. п., в котором определено скалярное произведение, удовлетворяющее перечисленным аксиомам, называется евклидовым пространством; оно может быть как конечномерным (n-мерным), так и бесконечномерным. Бесконечномерное евклидово пространство обычно называют гильбертовым пространством. Длина |x| вектора x и угол  между векторами х и у евклидова пространства определяются через скалярное произведение формулами

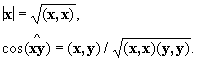
  Примером евклидова пространства может служить обычное трёхмерное пространство со скалярным произведением, определяемым в векторном исчислении. Евклидово n-мepное (арифметическое) пространство Eⁿ получим, определяя в n-мepном арифметическом В. п. скалярное произведение векторов x = (l₁, …, l_n) и y = (m₁, …, m_n) соотношением

  (x, y) = l₁m₁ + l₂m₂ +… + l_nm_n.    (2)

  При этом требования 1)—4), очевидно, выполняются.

  В евклидовых пространствах вводится понятие ортогональных (перпендикулярных) векторов. Именно векторы х и у называются ортогональными, если их скалярное произведение равно нулю: (х, у) = 0. В рассмотренном пространстве Eⁿ условие ортогональности векторов x = (l₁, …, l_n) и y = (m₁, …, m_n), как это следует из соотношения (2), имеет вид:

  l₁m₁ + l₂m₂ +… + l_nm_n = 0. (3)

  Применение В. п. Понятие В. п. (и различные обобщения) широко применяется в математике и её приложениях к естествознанию. Пусть, например, R — множество всех решений линейного однородного дифференциального уравнения yⁿ + a₁(x) y ^{(n + 1)} + … + a_n (x) y = 0. Ясно, что сумма двух решений и произведение решения на число являются решениями этого уравнения. Таким образом, R удовлетворяет условиям А. Доказывается, что для R выполнено обобщённое условие В. Следовательно, R является В. п. Любой базис в рассмотренном В. п. называется фундаментальной системой решений, знание которой позволяет найти все решения рассматриваемого уравнения. Понятие евклидова пространства позволяет полностью геометризовать теорию систем однородных линейных уравнений:

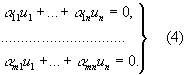
  Рассмотрим в евклидовом пространстве Eⁿ векторы a_i = (a_i1, a_i2, …, a_in), i = 1, 2,..., n и вектор-решение u = (u₁, u₂,..., u_n). Пользуясь формулой (2) для скалярного произведения векторов Eⁿ, придадим системе (4) следующий вид:

  (a_i, u) = 0, i = 1, 2, …, m.   (5)

  Из соотношений (5) и формулы (3) следует, что вектор-решение u ортогонален всем векторам a_i. Иными словами, этот вектор ортогонален линейной оболочке векторов a_i, то есть решение u есть любой вектор из ортогонального дополнения линейной оболочки векторов a_i. Важную роль в математике и физике играют и бесконечномерные линейные пространства. Примером такого пространства может служить пространство С непрерывных функций на отрезке с обычной операцией сложения и умножения на действительные числа. Упомянутое выше пространство всех многочленов является подпространством пространства С.

  Лит.: Александров П. С., Лекции по аналитической геометрии, М., 1968; Гельфанд И, М., Лекции по линейной алгебре, М. — Л., 1948.

  Э. Г. Позняк.