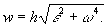Вращательное движение твёрдого тела, 1) вращательное движение вокруг оси — движение твёрдого тела, при котором какие-нибудь две его точки А. и В остаются всё время неподвижными (см. рис.). Прямая AB, проходящая через эти точки, называется осью вращения; все точки тела при В. д. описывают окружности в плоскостях, перпендикулярных к оси вращения, и с центрами, лежащими на этой оси. Тело, совершающее В. д., имеет одну степень свободы и его положение определяется углом φ между проведёнными через ось вращения неподвижной полуплоскостью и полуплоскостью, жёстко связанной с телом и вращающейся вместе с ним. Основные кинематические характеристики В. д. тела — его угловая скорость ω и угловое ускорение ε. Для любой точки тела, отстоящей от оси на расстоянии h, линейная скорость v = hω, касательное ускорение wτ = hω, нормальное ускорение wn = hω2 и полное ускорение

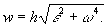
Основными динамическими характеристиками В. д. тела являются его кинетический момент относительно оси вращения Kz = Izω (см. Момент количества движения) и кинетическая энергия Т = 1/2 Izω2, где Iz — момент инерции тела относительно оси вращения. Закон вращения определяется из основного уравнения Iz ε = Mz, где Mz — вращающий момент (см. Момент силы).
2) Вращательное движение вокруг точки (или сферическое движение) — движение твёрдого тела, при котором какая-то одна его точка О остаётся неподвижной, а все другие точки движутся по поверхности сфер, имеющих центр в точке О. При таком В. д. тела любое его элементарное перемещение представляет собой элементарный поворот вокруг некоторой оси, проходящей через точку О и называется мгновенной осью вращения. Со временем эта ось, в отличие от неподвижной, непрерывно изменяет своё направление. В результате В. д. тела слагается из серии элементарных поворотов вокруг непрерывно меняющих своё направление мгновенных осей. Пример такого В. д. тела даёт движение гироскопа.
С. М. Тарг.
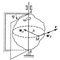
Рисунок к ст. Вращательное движение.