Гомотетия (от гомо... и греч. thetós — расположенный) (математическая), преобразование, в котором каждой точке М (плоскости или пространства) ставится в соответствие точка M', лежащая на OM, О — фиксированная точка (рис. 1), называемая центром Г., причём отношение OM' : OM = l одно и то же для всех точек М, отличных от О (при этом отношение OM' : OM считается положительным, если точки M' и М лежат по одну сторону от О, и отрицательным в противном случае). Число l называется коэффициентом Г. При l< 0 Г. называется обратной; при l = -1 Г. превращается в преобразование симметрии относительно точки О. При Г. прямая переходит в прямую, сохраняется параллельность прямых и плоскостей, сохраняются углы (линейные и двугранные); каждая фигура переходит в фигуру, ей подобную (рис. 2), верно и обратное утверждение. Г. может быть определена как аффинное преобразование, при котором прямые, соединяющие соответственные точки, проходят через одну точку (центр Г. ). Г. применяется для увеличения изображений (проекционный фонарь, кино).
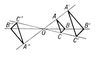
Рис. 2 к ст. Гомотетия.
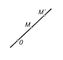
Рис. 1 к ст. Гомотетия.