Десятичная дробь, дробь, знаменатель которой есть целая степень числа 10. Д. д. пишут без знаменателя, отделяя в числителе справа запятой столько цифр, сколько нулей содержится в знаменателе. Например,

В такой записи часть, стоящая слева от запятой, обозначает целую часть дроби, первая цифра после запятой — количество десятых долей, вторая — количество сотых и т.д. Десятичная запись рациональных чисел, знаменатель которых не имеет других простых множителей, кроме 2 и 5, содержит конечное количество цифр (например, ⁴/₂₅ = 0,16); в общем случае цифры в десятичной записи рационального числа, начиная с некоторого места, периодически повторяются (такое число представляется бесконечной периодической дробью, например, ⁷/₆ = 1,1666...); иррациональные числа представляются непериодическими бесконечными десятичными дробями, например

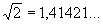
Во всех случаях Д. д. a_ka_k-1... a₀, b₁b₂... может быть записана в виде:

где а_к, a_k-1,..., a₀, b₁, b₂,... — цифры 0, 1, 2,..., 9 (a_k ¹ 0) в соответствующем разряде числа; например

т. е. здесь a₂ = 3, a₁ = 8, a₀ = 2, b₁ = 1, b₂ = 2, b₃ = 7, b₄ = 4. Д. д. применялись уже в 14—15 вв. Самаркандский математик аль-Каши в 1427 описал систему Д. д. В Европе Д. д. ввёл в употребление С. Стевин (1584.)