Квантование пространственное в квантовой механике, дискретность возможных пространственных ориентаций момента количества движения атома (или др. частицы или системы частиц) относительно любой произвольно выбранной оси (оси z). К. п. проявляется в том, что проекция Мг момента М на эту ось может принимать только дискретные значения, равные целому (0, 1, 2,...) или полуцелому (1/2, 3/2,5/2,...) числу m, помноженному на Планка постоянную 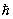 ,
, 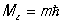 . Две другие проекции момента Mx и Му остаются при этом неопределёнными, т. к., согласно основному положению квантовой механики, одновременно точные значения могут иметь лишь величина момента и одна из его проекций. Для орбитального момента количества движения m (ml) может принимать значения 0, ± 1, ± 2,... ± l, где l = 0, 1, 2... определяет квадрат момента Ml (т. е. его абсолютную величину):
. Две другие проекции момента Mx и Му остаются при этом неопределёнными, т. к., согласно основному положению квантовой механики, одновременно точные значения могут иметь лишь величина момента и одна из его проекций. Для орбитального момента количества движения m (ml) может принимать значения 0, ± 1, ± 2,... ± l, где l = 0, 1, 2... определяет квадрат момента Ml (т. е. его абсолютную величину):  . Для полного момента количества движения М (орбитального плюс спинового) m (ml) принимает значения с интервалом в 1 от — j до + j, где j определяет величину полного момента:
. Для полного момента количества движения М (орбитального плюс спинового) m (ml) принимает значения с интервалом в 1 от — j до + j, где j определяет величину полного момента: 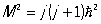 и может быть целым или полуцелым числом.
и может быть целым или полуцелым числом.
Если атом помещается во внешнее магнитное поле H, то появляется выделенное направление в пространстве — направление поля (которое и принимают за ось z). В этом случае К. п. приводит к квантованию проекции mн магнитного момента атома m на направление поля, т.к. магнитный момент пропорционален механическому моменту количества движения (отсюда название m — «магнитное квантовое число»). Это приводит к расщеплению уровней энергии атома в магнитном поле вследствие того, что к энергии атома добавляется энергия его магнитного взаимодействия с полем, равная — mHH (см. Зеемана эффект).
В. И. Григорьев.
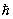 ,
, 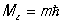 . Две другие проекции момента Mx и Му остаются при этом неопределёнными, т. к., согласно основному положению квантовой механики, одновременно точные значения могут иметь лишь величина момента и одна из его проекций. Для орбитального момента количества движения m (ml) может принимать значения 0, ± 1, ± 2,... ± l, где l = 0, 1, 2... определяет квадрат момента Ml (т. е. его абсолютную величину):
. Две другие проекции момента Mx и Му остаются при этом неопределёнными, т. к., согласно основному положению квантовой механики, одновременно точные значения могут иметь лишь величина момента и одна из его проекций. Для орбитального момента количества движения m (ml) может принимать значения 0, ± 1, ± 2,... ± l, где l = 0, 1, 2... определяет квадрат момента Ml (т. е. его абсолютную величину):  . Для полного момента количества движения М (орбитального плюс спинового) m (ml) принимает значения с интервалом в 1 от — j до + j, где j определяет величину полного момента:
. Для полного момента количества движения М (орбитального плюс спинового) m (ml) принимает значения с интервалом в 1 от — j до + j, где j определяет величину полного момента: 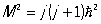 и может быть целым или полуцелым числом.
и может быть целым или полуцелым числом.