 говорят, что она регулярно сходится, если для всякого натурального числа n соблюдается условие
говорят, что она регулярно сходится, если для всякого натурального числа n соблюдается условиеКонструктивная математика, абстрактная наука о конструктивных процессах, человеческой способности осуществлять их и о их результатах — конструктивных объектах. Абстрактность К. м. проявляется прежде всего в том, что в ней систематически применяются две абстракции: абстракция потенциальной осуществимости и абстракция отождествления. Абстракцию потенциальной осуществимости используют, когда отвлекаются от практических ограничений конструктивных возможностей в пространстве, времени и материале. Абстракцию отождествления используют, когда говорят о двух в том или ином смысле одинаковых объектах как об одном и том же объекте. В К. м. не применяется характерная для теоретико-множественной математики абстракция актуальной бесконечности, связанная с рассмотрением никогда не завершаемых процессов как бесконечно продолженных и тем самым как бы завершенных.
Конструктивный процесс, результатом которого является объект, одинаковый с А, называется построением объекта А. Высказывания, связанные с человеческой способностью осуществлять конструктивные процессы, часто формулируются в К. м. в виде теорем существования, утверждающих, что существует объект, удовлетворяющий каким-то требованиям. Под этим подразумевают, что построение такого объекта потенциально осуществимо, т. е. что владеют способом его построения. Это понимание теорем существования отличается от их понимания в теоретико-множественной математике, что вынуждает строить для К. м. свою логику, отличную от обслуживающей теоретико-множественную математику классической математической логики, — конструктивную математическую логику.
Понятия конструктивного процесса и конструктивного объекта не определяются в К. м. В таких общих определениях и нет надобности, поскольку в К. м. обычно имеют дело не с конструктивными процессами и конструктивными объектами вообще, а с определёнными видами тех и других.
Простейшим видом конструктивных объектов являются слова в фиксированном алфавите, т. е. ряды букв этого алфавита (слово «буква» понимается здесь как «элементарный знак», т. е. как «знак, частями которого мы не интересуемся»; алфавит — это набор букв). Конструктивный процесс, результатом которого является слово, состоит в данном случае в выписывании этого слова буква за буквой. Частным случаем слов являются натуральные числа, которые мы рассматриваем как слова в алфавите 01, начинающиеся с нуля и, кроме того, нуля не содержащие, т. е. как слова 0, 01, 011, 0111,... Добавляя к этому алфавиту знак минус «—» и знак дроби «/», получают возможность строить рациональные числа как некоторые слова в алфавите 01 — /. Т. о., рациональные числа оказываются конструктивными объектами.
Естественно, возник вопрос о построении действительных чисел в рамках К. м. и, далее, вопрос о включении математического анализа в эти рамки. Эти цели достигнуты на основе уточнённого понятия алгоритма. Каким из известных уточнений этого понятия (Тьюринга машина, рекурсивные функции, нормальные алгорифмы) здесь пользоваться, при этом несущественно. В дальнейшем под «алгорифмом» будет пониматься нормальный алгорифм.
Конструктивной последовательностью рациональных (натуральных) чисел будет называться алгорифм, перерабатывающий всякое натуральное число в рациональное (натуральное) число. Без существенного ограничения общности можно считать конструктивную последовательность рациональных чисел алгорифмом в алфавите 01 — /ab. Запись такого алгорифма будет осуществляться как слово в алфавите 01. О конструктивной последовательности рациональных чисел 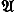 говорят, что она регулярно сходится, если для всякого натурального числа n соблюдается условие
говорят, что она регулярно сходится, если для всякого натурального числа n соблюдается условие
|(n) - (n+1)|£ 2-n-1.
Записи регулярно сходящихся последовательностей рациональных чисел называют конструктивными действительными числами (КДЧ). Естественным образом определяются равенство двух КДЧ, порядковые отношения между ними, а также арифметическими действия над ними и операция взятия абсолютной величины. Арифметические операции оказываются алгорифмическими: имеется, например, алгорифм, перерабатывающий всякую пару КДЧ в сумму этих КДЧ. С другой стороны, невозможен алгорифм, распознающий КДЧ среди слов в алфавите 01; невозможен алгорифм, распознающий равенство КДЧ.
Далее, на основе алгоритмов теории можно определить понятие конструктивной последовательности КДЧ. Для всякой такой последовательности оказывается возможным построить КДЧ, не равное ни одному члену этой последовательности. Это — конструктивный аналог теоремы Кантора о несчётности континуума.
Могут быть определены понятия конструктивной сходимости конструктивной последовательности КДЧ в себе и к КДЧ. Имеет место теорема полноты, утверждающая, что всякая конструктивная последовательность КДЧ, конструктивно сходящаяся в себе, конструктивно сходится к некоторому КДЧ. Однако конструктивный аналог известной теоремы о сходимости ограниченной возрастающей последовательности опровергается на примере.
Согласно определению, КДЧ — слова в алфавите 01. Алгорифмы над этим алфавитом можно применять к КДЧ, что открывает возможность строить функцию от действительного переменного как алгорифм, перерабатывающий КДЧ в КДЧ. Надо только, чтобы такой алгорифм был согласован с равенством — равные КДЧ он должен перерабатывать в равные КДЧ. Т. о., получается следующее определение — алгорифм F над алфавитом 01 есть конструктивная функция действительного переменного, если соблюдаются следующие условия: 1) F перерабатывает всякое КДЧ, к которому он применим, в КДЧ; 2) всякий раз, когда F применим к каким-либо КДЧ х, он применим и ко всякому КДЧ у, равному х, и КДЧ F (x) и F (y) равны.
На основе этого определения была разработана конструктивная теория функций действительного переменного. Одним из наиболее интересных её результатов является теорема о непрерывности конструктивных функций: всякая конструктивная функция действительного переменного непрерывна всюду, где она определена. Вместе с тем выяснено, что в теории конструктивных функций не имеют место аналоги классических теорем Вейерштрасса и Кантора о непрерывных функциях на сегменте. В частности, были построены: 1) неограниченная конструктивная (и потому непрерывная) функция на сегменте [0,1]; 2) ограниченная на этом сегменте конструктивная функция, не имеющая точной верхней границы; 3) конструктивная функция, имеющая на сегменте [0,1] точную верхнюю границу, но не достигающая её; 4) ограниченная на сегменте [0,1] конструктивная функция, не являющаяся равномерно непрерывной ни на каком сегменте, содержащемся в сегменте [0,1]. Эти результаты выявляют глубокое отличие конструктивного математического анализа от анализа теоретико-множественного.
В настоящее время (70-е гг. 20 в.) успешно разрабатываются многие отделы К. м.: конструктивные теории дифференцирования и интегрирования, конструктивная теория метрических пространств, конструктивный функциональный анализ, конструктивная теория функций комплексного переменного и др.
Лит.: Марков А. А., Теория алгорифмов, «Тр. Математического института АН СССР», 1954, т. 42; Проблемы конструктивного направления в математике, в. 1—5, там же, 1958, т. 52; 1962, т. 67; 1964, т. 72; 1967, т. 93; 1970, т. 113; Фан Динь Зиеу, Некоторые вопросы конструктивного функционального анализа, там же, 1970, т. 114.
А. А. Марков.