Кристаллы (от греч. krýstallos, первоначально — лёд, в дальнейшем — горный хрусталь, кристалл), твёрдые тела, имеющие естественную форму правильных многогранников (рис. 1). Эта форма — следствие упорядоченного расположения в К. атомов, образующих трёхмерно-периодическую пространственную укладку — кристаллическую решетку. К. — равновесное состояние твёрдых тел. Каждому химическому веществу, находящемуся при данных термодинамических условиях (температуре, давлении) в кристаллическом состоянии, соответствует определённая кристаллическая атомная структура. К. обладают той или иной симметрией атомной структуры, соответствующей ей макроскопической симметрией внешней формы, а также анизотропией физических свойств. К., выросший в неравновесных условиях и не имеющий правильной огранки или потерявший её в результате той или иной обработки, сохраняет основной признак кристаллического состояния — решётчатую атомную структуру и все определяемые ею свойства.
Большинство природных или технических твёрдых материалов являются поликристаллическими, они состоят из множества отдельных, беспорядочно ориентированных, мелких кристаллических зёрен, иногда называемых кристаллитами. Таковы, например, многие горные породы, технические металлы и сплавы. Одиночные кристаллы (природные или синтетические) называются монокристаллами.
К. образуются и растут чаще всего из жидкой фазы — раствора или расплава; возможно получение К. из газовой фазы или при фазовом превращении в твёрдой фазе (см. Кристаллизация). В природе встречаются К. различных размеров — от громадных (до сотен кг) К. кварца (горного хрусталя), флюорита, полевого шпата до мелких К. алмаза и др. Для научных и технических целей разнообразные К. выращивают (синтезируют) в лабораториях и на заводах (см. Монокристаллы). Можно получить кристаллы и таких сложных природных веществ, как белки (рис. 1, в) и даже вирусы.
Геометрия К. Выросшие в равновесных условиях К. имеют форму правильных многогранников той или иной симметрии, грани К. — плоские, ребра между гранями прямолинейные. Углы между соответствующими гранями К. одного и того же вещества постоянны (рис. 2). В этом заключается первый закон геометрии кристаллографии — закон постоянства углов (Н. Стенон, 1669). Он формулируется и так: при росте К. грани его передвигаются параллельно самим себе. Измерение межгранных углов (гониометрия), до появления рентгеноструктурного анализа широко использовавшееся как средство идентификации химического состава К. (Е. С. Федоров, Грот), не потеряло своего значения (см. Гониометр). Второй основной закон геометрии кристаллографии — закон целых чисел (см. Гаюи закон) — является макроскопическим следствием микропериодичности кристаллического вещества, которое состоит из повторяющихся в пространстве элементарных ячеек, имеющих, в общем случае, форму параллелепипеда с ребрами (периодами кристаллической решётки), равными а, в, с. Всякая атомная плоскость кристаллической решётки (которой соответствует грань К.) отсекает на осях координат целые числа периодов решётки k, т, n (рис. 3). Обратные им, также целые, числа (h, k, l) называются кристаллографическими индексами граней и атомных плоскостей (см. Миллеровские индексы). Как правило, К. имеет грани с малыми значениями индексов, например (100), (110), (311) и т. д. Величины (а, в, с периодов решётки и углов между ними a, b, g измеряются рентгенографически. Выбор осей координат производится по определённым правилам в соответствии с симметрией кристалла.
Кристаллические многогранники симметричны: их грани и ребра могут быть совмещены друг с другом с помощью операций симметрии. Каждая операция производится относительно плоскости оси или центра симметрии (рис. 4). Всего существует 32 класса симметрии кристаллических многогранников (32 точечные группы симметрии). Каждый класс характеризуется определённым набором элементов симметрии. Элементами симметрии точечных групп являются поворотные оси (рис. 4, а), центр симметрии (рис. 4, в), инверсионно поворотные оси 3, 4, 6, плоскости симметрии (рис. 4, б) (см. Симметрия кристаллов). 32 класса группируются в соответствии с наличием в них характерных элементов симметрии в семь сингоний: триклинную, моноклинную, ромбическую (низшие сингоний), тетрагональную, гексагональную, тригональную (средние), кубическую (высшая).
Совокупность кристаллографически одинаковых граней (т. е. совмещающихся друг с другом под действием операций симметрии данного класса) называются простой формой К. Всего существует 47 простых форм, в каждом классе К. могут реализоваться лишь некоторые из них. Тот или иной К. может быть огранён гранями одной простой формы (рис. 5, а), но чаще — той или иной комбинацией этих форм (рис. 5, б, в).
Если К. принадлежит к классу, содержащему лишь простые оси симметрии (но не содержащему плоскостей, центра симметрии или инверсионных осей), то он может кристаллизоваться в зеркально равных формах. Это явление называется энантиоморфизмом, а соответствующие энантиоморфные формы —«правой» и «левой» (рис. 6).
При неравновесных условиях образования К. их идеальная форма (габитус) может претерпевать изменения. Различия в условиях подвода вещества, скоростей роста, молекулярных процессов и т. п. при кристаллизации могут привести к исключительному многообразию форм К.: округлости граней и рёбер (рис. 7), возникновению пластинчатых, игольчатых, нитевидных (рис. 8, а), ветвистых (дендритных) К. типа снежинок (рис. 8, б). Эти особенности используются в технике выращивания К. разнообразных форм (дендритных лент германия, тонких плёнок различных полупроводников). Некоторым К. уже в процессе выращивания придаётся форма требуемого изделия — трубы, стержня (рис. 9), пластинки. Если в объёме расплава образуется сразу большое количество центров кристаллизации, то разрастающиеся К., встречаясь друг с другом, приобретают форму неправильных зёрен.
Атомная структура К. Внешняя форма К., принадлежность его к тому или иному классу и сингоний определяются его кристаллической решёткой с характерной для неё симметрической операцией бесконечно повторяющихся переносов (трансляций). Вследствие этого, кроме упоминавшихся выше операции симметрии (поворотов вокруг осей симметрии, плоскостей, центра), в структуре К. возможны операции симметрии с бесконечным переносом, например винтовые оси симметрии, плоскости скользящего отражения и т. п. То или иное определённое их сочетание есть пространственная (фёдоровская) группа симметрии структуры кристалла. Всего существует 230 фёдоровских групп, распределённых среди 32 классов симметрии К.
Методы структурного анализа К. (рентгеноструктурный анализ, электронография, нейтронография) позволяют определить размеры элементарной ячейки К., федоровскую группу, расположение атомов в ячейке (расстояние между ними), характер тепловых колебаний атомов, распределение электронной плотности между атомами, ориентацию магнитных моментов и т. п. Уже изучена атомная кристаллическая структура более 20 тыс. соединений — от К. элементов до сложнейших К. белков (см. табл. и рис. 10).
| Кристаллы | Периоды ячеек (Ǻ) | Число атомов в элементарной ячейке |
| Элементы, простейшие соединения. | 3—5 | ~10 |
| Неорганические соединения, простые молекулярные соединения | 5—15 | до 100 |
| Сложные молекулярные соединения (витамины, стероиды и др.) | 20—30 | до 1000 |
| Белки | до 100—200 | 103—104 |
| Вирусы | до 2000 | 106—109 |
Обобщение этого колоссального материала является предметом кристаллохимии. Кристаллические структуры классифицируют по их химическому составу, в основном определяющему тип химической связи, по соотношению компонент в химической формуле (например, элементы, соединения AX, AX2, ABX3 и т. п.), по взаимной координации атомов (слоистые, цепные, координационные решётки).
При изменении температуры или давления структура К. может изменяться. Некоторые кристаллические структуры (фазы) являются метастабильными. Существование у данного вещества нескольких кристаллических фаз, а значит и К. с разной структурой, называется полиморфизмом (белое и серое олово, алмаз и графит, различные модификации кварца и т. п.). Наоборот, разные соединения могут иметь одинаковую кристаллическую структуру — быть изоструктурными (см. Изоморфизм).
Распределение К. по пространственным группам (соответственно по классам и сингониям) неравномерно. Как правило, чем проще химическая формула вещества, тем выше симметрия его К. Так, почти все металлы имеют кубическую или гексагональную структуру, то же относится к простым химическим соединениям, например щёлочно-галоидным и др. Усложнение химической формулы вещества ведёт к понижению симметрии его К. Органические (молекулярные) К. почти всегда относятся к низшим сингониям.
Тип химической связи между атомами в К. определяет многие их свойства. Ковалентные К. с локализованными на прочных связях электронами имеют высокую твёрдость, малую электропроводность, большие показатели преломления. Наоборот, металлические К. со свободными электронами хорошо проводят электрический ток и тепло, пластичны, непрозрачны. Промежуточные характеристики — у ионных К. Наиболее слабые (вандер-ваальсовы) связи — в молекулярных К. Они легкоплавки, механические характеристики их низки. Атомную упорядоченность, более низкую, чем у К., имеют жидкие кристаллы, аморфные тела и стекла (см. Аморфное состояние, Полимеры).
Структура реальных К. Вследствие нарушения равновесных условий роста, захвата примесей при кристаллизации, под влиянием различного рода воздействий идеальная структура К. всегда имеет те или иные нарушения. К ним относят точечные дефекты, т. е. вакансии (пропуски атомов), замещения атомов основной решётки атомами примесей, внедрение в решётку инородных атомов; линейные дефекты, т. е. дислокации (нарушение порядка упаковки атомных слоев, рис. 11), и др. Дозируемое введение небольших количеств атомов примеси, замещающих атомы основной решётки, широко используется в технике для изменения свойств К., например введение в кристаллы Ge и Si атомов III и V групп периодической системы элементов позволяет получать полупроводники с дырочной и электронной электропроводностью. Др. пример — К., применяющиеся в квантовой электронике: рубин, состоящий из AI2O3 и примеси (0,05%) Cr; гранат — из Y3Al5O12 и примеси (0,5%) Nd и др. (см. Лазерные материалы).
При росте К. их грани имеют различные коэффициент захвата примесей, что определяет секториальное строение К. (рис. 12). Может происходить и периодическое изменение концентрации захватываемой примеси, что даёт зонарную структуру (рис. 13) (см. Кристаллизация). Кроме того, в процессе роста почти неизбежно образуются макроскопические дефекты — включения, напряжённые области и т. п.
Все реальные К. имеют мозаичное строение: они разбиты на блоки мозаики — небольшие (10-4 см) области, в которых порядок почти идеален, но которые разориентированы по отношению друг к другу на малые углы (приблизительно несколько минут).
Физические свойства К. Основной отличительный признак свойств К. — их анизотропия, т. е. зависимость от направления, тогда как в изотропных (жидкостях, аморфных твёрдых телах) или псевдоизотропных (поликристаллы) телах свойства от направлений не зависят. При рассмотрении многих свойств К. дискретность атомной структуры К. не играет роли, и К. можно рассматривать как однородную анизотропную среду. Симметрию ряда свойств кристаллов можно описать с помощью предельных точечных групп симметрии. Соподчинённость классов симметрии К. и симметрии их физических свойств, а также связь симметрии свойств с симметрией внешних воздействий (например, внешних полей) определяются Кюри принципом и Неймана принципом. Наличие или отсутствие тех или иных элементов точечной симметрии позволяет указать, в каких из 32 классов возможны те или иные свойства, а также определяет вид тензоров, описывающих эти свойства. Например, пироэлектричество возможно в К. 10 классов, имеющих одну ось симметрии или совпадающую с ней плоскость симметрии; пьезоэлектричество возможно в К. 20 классов, не имеющих центра симметрии, и т. п.
Для К. данного класса можно указать симметрию его свойств. Так, кубические К. изотропны в отношении прохождения света, электро- и теплопроводности, теплового расширения, но анизотропны в отношении упругих, электрооптических, пьезоэлектрических свойств. Для К. средних сингоний (например, кварц) главные константы тензоров, описывающих свойства, определяются их значениями вдоль и перпендикулярно главной оси симметрии, а в промежуточных направлениях могут быть вычислены из главных. Наиболее анизотропны кристаллы низших сингоний.
Все свойства К. связаны между собой и обусловлены его кристаллической структурой — расположением атомов и силами связи между ними. Эти силы обусловлены электронным строением атомов или молекул, составляющих кристаллическую решётку. При этом ряд свойств К. зависит непосредственно от межатомных взаимодействий, например тепловые, упругие, акустические свойства. Электрические, магнитные, оптические свойства существенно зависят от распределения электронов по уровням энергии (от электронного спектра). Так, очень высокая электропроводность металлов или относительно низкая у диэлектриков и полупроводников, связаны с высокой или низкой концентрацией электронов проводимости (см. Твёрдое тело). В некоторых К. ионы, образующие решётку, располагаются так, что К. оказывается самопроизвольно (спонтанно) электрически поляризованным (пироэлектрики). Большая величина такой поляризации характерна для сегнетоэлектриков.
Многие свойства К. решающим образом зависят не только от симметрии, но и от количества и типов дефектов в К. Таковы прочность и пластичность, окраска, люминесцентные свойства и др. Из-за наличия дислокаций пластическое деформирование К. происходит при напряжениях, в десятки и сотни раз меньших теоретически вычисленного. В бездислокационных К. (германия, кремния) прочность в 10—100 раз больше, чем прочность в обычных К. Окраска многих К. (поглощение света в них) связана с наличием в них тех или иных примесных атомов.
Применение К. Пьезо- и сегнетоэлектрические К. (кварц и др.) применяются в радиотехнике. Большая область полупроводниковой электроники (радиотехнические и счётно-решающие устройства) основана на полупроводниковых К. (германий, кремний и др.) или микросхемах на них (см. Микроэлектроника). В запоминающих устройствах громадной ёмкости используются К. магнитодиэлектриков и различных типов ферритов. Исключительное значение имеют К. для квантовой электроники (рубин, иттриево-алюминиевый гранат и др.). В технике управления световыми пучками используют К., обладающие электрооптическими свойствами. Для измерения слабых изменений температуры применяются пироэлектрические К., для измерения механических и акустических воздействий — пьезоэлектрики, пьезомагнетики (см. Пьезомагнетизм), пьезорезисторы и т. п. Высокие механические свойства сверхтвёрдых К. (алмаз и др.) используются в обработке материалов и бурении; К. рубина, сапфира и др. применяют в качестве опорных элементов в часах и др. точных приборах. Ювелирная промышленность использует не только природные драгоценные камни, но всё больше и синтетические К. Номенклатура промышленного производства различных синтетических К. исчисляется тысячами наименований, производство некоторых К. достигает десятков и сотен тонн в год.
Лит.: Шубников А. В., Флинт Е. А., Бокий Г. Б., Основы кристаллографии, М.— Л., 1940; Шаскольская М., Кристаллы, М., 1959; Костов И., Кристаллография, пер. с болг., М., 1965; Банн Ч., Кристаллы, пер. с англ., М., 1970; Най Дж., Физические свойства кристаллов и их описание при помощи тензоров и матриц, пер. с англ., 2 изд., М., 1967. См. также лит. при статьях Кристаллизация, Монокристаллы, Кристаллография, Кристаллофизика, Кристаллохимия.
М. П. Шаскольская, Б. К. Вайнштейн.
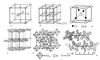
Рис. 10. Атомная структура меди (а), NaCl (б), Cu2O (в), графита (г), К2PtCl6 (д), фталоцианина (е).

Рис. 8б. Дендриты хлористого аммония.
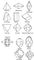
Рис. 5. а — некоторые простые формы кристаллов; б — принцип образования комбинаций простых форм; в — реально наблюдаемые огранки некоторых кристаллов.
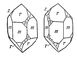
Рис. 6. «Правый» и «левый» кварц.

Рис. 13. Зонарная структура кристалла.

Рис. 9. Монокристальная «буля» рубина (длина 20 см).

Рис. 1в. Кристаллы белка каталазы (увеличено).

Рис. 12. Секториальное строение кристалла.

Рис. 3. К закону целых чисел.

Рис. 1а. Природные кристаллы турмалина.

Рис. 11. Реальная дислокационная структура кристаллов кварца — получено методом рентгеновской топографии (увеличено).

Рис. 7. Вицинальные формы и холмики роста на грани кварца.
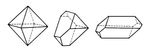
Рис. 2. Постоянство межгранных углов данного кристалла при разном развитии граней.

Рис. 1б. Монокристалл сегнетовой соли.
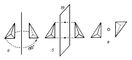
Рис. 4. Простейшие элементы симметрии кристаллов; а — ось симметрии (в данном случае второго порядка) совмещает фигуру с собой поворотом на 360°/N (N — порядок оси симметрии); б — плоскость симметрии m — совмещает фигуру «отражением»; в — центр симметрии — действует как поворот и отражение одновременно.

Рис. 8а. Нитевидные кристаллы AIN (электронномикроскопическое изображение, увеличено).

Рис. 1г. Микромонокристалл германия (увеличено).