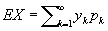
Математическое ожидание, среднее значение, одна из важнейших характеристик распределения вероятностей случайной величины. Для случайной величины X, принимающей последовательность значений y1, y2, ..., yk, ... с вероятностями, равными соответственно p1, p2, ..., pk, …, М. о. определяется формулой
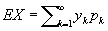
(в предположении, что ряд  сходится). Так, например, если Х — число очков, выпадающее на верхней грани игральной кости (X принимает каждое из значений 1, 2, 3, 4, 5, 6 с вероятностью 1/6), то
сходится). Так, например, если Х — число очков, выпадающее на верхней грани игральной кости (X принимает каждое из значений 1, 2, 3, 4, 5, 6 с вероятностью 1/6), то 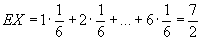 .
.
Для случайной величины, имеющей плотность вероятности р(у), М. о. определяется формулой
 .
.
М. о. характеризует расположение значений случайной величины. Полностью эта роль М. о. разъясняется больших чисел законом. При сложении случайных величин их М. о. складываются, при умножении двух независимых случайных величин их М. о. перемножаются. М. о. случайной величины eitX, то есть f (t) = Eeitxz, где t — действительное число, носит название характеристической функции.
Лит.: Гнеденко Б. В., Курс теории вероятностей, 4 изд., М., 1965.
Ю. В. Прохоров.