Огибающая семейства линий на плоскости (поверхностей в пространстве), линия (поверхность), которая в каждой своей точке касается одной линии (поверхности) семейства, геометрически отличной от О. в сколь угодно малой окрестности точки касания (см. Семейство линий, Семейство поверхностей). Уравнение О. семейства линий на плоскости, определяемого уравнением f (х, у, С) = 0, содержащим параметр С, можно получить [в предположении, что f (х, у, С) имеет непрерывные частные производные 1-го порядка по всем трём аргументам], исключив параметр С из системы:
f (x, у, С) = 0, f 'c (х, у, С) = 0.
Это исключение, вообще говоря, даёт не только О., но и геометрическое место особых точек линий семейства, т. е. точки, для которых одновременно f 'x = 0, f 'y = 0.
Примеры (на плоскости): а) семейство окружностей радиуса R, центры которых лежат на одной прямой, имеет в качестве О. пару прямых, параллельных линии центров и отстоящих от неё в ту и другую сторону на расстояние R (см. рис. 1); б) всякая кривая служит О. для семейства своих касательных и семейства своих кругов кривизны; в) если в каждой точке кривой построить к ней нормаль, то для полученного семейства прямых О. будет эволюта (см. Эволюта и эвольвента) данной кривой (на рис. 2 изображена эволюта эллипса).
В пространстве для семейств поверхностей могут существовать О., касающиеся поверхностей семейства в точках или же вдоль некоторых линий. Примеры: а) семейство сфер радиуса R с центрами, расположенными на одной прямой, имеет своей О. круглый цилиндр радиуса R, ось которого есть линия центров (касание цилиндра с каждой сферой — по окружности); б) семейство сфер радиуса R, центры которых лежат в одной плоскости, имеет О. пару плоскостей, параллельных плоскости центров и отстоящих от неё в ту и другую сторону на расстояние R (касание плоскостей каждой сферой — точке).
Понятие О. имеет значение не только в геометрии, но и в некоторых вопросах математического анализа (особые решения в теории дифференциальных уравнений), теоретической физики (в оптике — каустика, фронт волны).
Лит.: Толстов Г. П., К отысканию огибающей семейства плоских кривых, «Успехи математических наук», 1952, т. 7, в. 4; Ла Валле-Пуссен Ш.-Ж. де, Курс анализа бесконечно малых, пер. с франц., т. 2, Л. — М., 1933; Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., ч. 1, М., 1971.
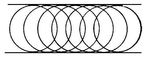
Рис. 1 к ст. Огибающая.
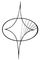
Рис. 2 к ст. Огибающая.