Относительности теория, физическая теория, рассматривающая пространственно-временные свойства физических процессов. Закономерности, устанавливаемые О. т., являются общими для всех физических процессов, поэтому часто о них говорят просто как о свойствах пространства-времени. Как было установлено А. Эйнштейном, эти свойства зависят от гравитационных полей (полей тяготения), действующих в данной области пространства-времени. Свойства пространства-времени при наличии полей тяготения исследуются в общей теории относительности (ОТО), называются также теорией тяготения. В частной теории относительности рассматриваются свойства пространства-времени в приближении, в котором эффектами тяготения можно пренебречь. Логически частная О. т. есть частный случай ОТО, откуда и происходит её название. Исторически развитие теории происходило в обратном порядке; частная О. т. была сформулирована Эйнштейном в 1905, окончательная формулировка ОТО была дана им же в 1916. Ниже излагается частная О. т., называется в литературе также теорией относительности Эйнштейна, просто О. т., или специальной теорией относительности (история её возникновения изложена в последнем разделе).

  Основные черты теории относительности

  Явления, описываемые О. т. и называемые релятивистскими (от лат. relatio — отношение), проявляются при скоростях движения тел, близких к скорости света в вакууме с = (2,997924562 ± 0,000000011) ´ 10¹⁰ см/сек. При таких скоростях (называемых релятивистскими) зависимость энергии Е тела от его скорости v описывается уже не формулой классической механики Е_кин = mu²/2, а релятивистской формулой

 (1)

  Масса т, входящая в эту формулу, в О. т. называется также массой покоя. Из (1) видно, что энергия тела стремится к бесконечности при скорости u, стремящейся к с, поэтому если масса покоя не равна нулю, то скорость тела всегда меньше с, хотя при Е >> mc ² она может стать сколь угодно близкой к с. Это непосредственно наблюдается на ускорителях протонов и электронов, в которых частицам сообщаются энергии, много большие mc ², и поэтому они движутся со скоростью, практически равной с. Со скоростью света всегда движутся частицы, масса покоя которых равна нулю (фотоны — кванты света, нейтрино). Скорость с является предельной скоростью передачи любых взаимодействий и сигналов из одной точки пространства в другую.

  Существование предельной скорости вызывает необходимость глубокого изменения обычных пространственно-временных представлений, основанных на повседневном опыте. Рассмотрим следующий мысленный опыт. Пусть в вагоне, движущемся со скоростью u относительно полотна железной дороги, посылается световой сигнал в направлении движения. Скорость сигнала для наблюдателя в вагоне равна с. Если бы длины и времена, измеряемые любым наблюдателем, были одинаковы, то выполнялся бы закон сложения скоростей классической механики и для наблюдателя, стоящего у полотна, скорость сигнала была бы равна с + u, т. е. была бы больше предельной. Противоречие устраняется тем, что в действительности с точки зрения наблюдателя, относительно которого физическая система движется со скоростью u, все процессы в этой системе замедляются в  раз (это явление называется замедлением времени), продольные (вдоль движения) размеры тел во столько же раз сокращаются и события, одновременные для одного наблюдателя, оказываются неодновременными для другого, движущегося относительно него (т. н. относительность одновременности). Учёт этих эффектов приводит к закону сложения скоростей, при котором предельная скорость оказывается одинаковой для всех наблюдателей.

  Характерное для О. т. явление замедления времени может принимать огромные масштабы. В опытах на ускорителях и в космических лучах образуются распадающиеся (нестабильные) частицы, движущиеся со скоростью, близкой к скорости света. В результате замедления времени (с точки зрения земного наблюдателя) времена их распада и, следовательно, проходимые ими (от рождения до распада) расстояния увеличиваются в тысячи и десятки тысяч раз по сравнению с теми, которые частицы пролетали бы, если бы эффект замедления времени отсутствовал.

  Из релятивистской формулы для энергии следует, что при малых скоростях (u << с) энергия тела равна

  Второй член справа есть обычная кинетическая энергия, первый же член показывает, что покоящееся тело обладает запасом энергии E_o = mc ², называющейся энергией покоя (т. н. принцип эквивалентности энергии и массы, или принцип эквивалентности Эйнштейна).

  В ядерных реакциях и процессах превращений элементарных частиц значительная часть энергии покоя может переходить в кинетическую энергию частиц. Так, источником энергии, излучаемой Солнцем, является превращение четырёх протонов в ядро гелия; масса ядра гелия меньше массы четырёх протонов на 4,8×10^–26г, поэтому при каждом таком превращении выделяется 4,3×1^–5эрг кинетической энергии, уносимой излучением. За счёт излучения Солнце теряет в 1 сек 4×10⁷ т своей массы.

  О. т. подтверждена обширной совокупностью фактов и лежит в основе всех современных теорий, рассматривающих явления при релятивистских скоростях. Уже последовательная теория электромагнитных, в частности оптических, явлений, описываемых классической электродинамикой (см. Максвелла уравнения), возможна только на основе О. т. Теория относительности лежит также в основе квантовой электродинамики, теорий сильного и слабого взаимодействий элементарных частиц. Законы движения тел при релятивистских скоростях рассматриваются в релятивистской механике, которая при скоростях u << с переходит в классическую механику Ньютона. Квантовые законы движения релятивистских микрочастиц рассматриваются в релятивистской квантовой механике и квантовой теории поля.

  Принцип относительности и другие принципы инвариантности

  В основе О. т. лежит принцип относительности, согласно которому в физической системе, приведённой в состояние свободного равномерного и прямолинейного движения относительно системы, условно называется «покоящейся», для наблюдателя, движущегося вместе с системой, все процессы происходят по тем же законам, что и в «покоящейся» системе. Говорят, что движущаяся система получается из «покоящейся» преобразованием движения и что принцип относительности выражает инвариантность (независимость) законов природы относительно преобразований движения.

  Справедливость принципа относительности означает, что различие между состояниями покоя и равномерного прямолинейного движения не имеет физического содержания. Если физическая система В движется равномерно и прямолинейно (со скоростью V ) относительно системы А, то с тем же правом можно считать, что А движется относительно В (со скоростью V). Термин «принцип относительности» связан с тем, что если преобразованию движения подвергнуть систему движущихся тел, то все относительные движения этих тел останутся неизменными.

  Наряду с принципом относительности из опыта известны и др. принципы инвариантности, или, как ещё говорят, симметрии, законов природы. Любой физический процесс происходит точно так же:

  если осуществить его в любой др. точке пространства; эта симметрия выражает равноправие всех точек пространства, однородность пространства;

  если систему, в которой происходит процесс, повернуть на произвольный угол; эта симметрия выражает равноправие всех направлений в пространстве, изотропию пространства;

  если повторить процесс через некоторый промежуток времени; эта симметрия выражает однородность времени.

  Т. о., имеет место инвариантность законов природы по отношению к четырём типам преобразований: 1) переносу в пространстве, 2) вращению в пространстве, 3) сдвигу во времени, 4) преобразованию движения. Симметрии 1—4 выполняются точно только в изолированной от внешних воздействий системе, т. е. если можно пренебречь воздействием на систему внешних факторов; для реальных систем они справедливы лишь приближённо.

  Изучение свойств преобразований 1—2 составляет предмет евклидовой геометрии трёхмерного пространства, если рассматривать её как физическую теорию, описывающую пространственные свойства физических объектов (при этом под переносом следует понимать преобразование параллельного переноса).

  При скоростях тел u, сравнимых со скоростью с, обнаруживается тесная связь и математическая аналогия между преобразованиями 1, 3 и 2, 4. Это даёт основание говорить об О. т., в которой все преобразования 1—4 следует рассматривать совместно, как о геометрии пространства-времени. Содержанием О. т. является рассмотрение свойств преобразований 1—4 и следствий из соответствующих принципов инвариантности. Математически О. т. является обобщением геометрии Евклида — геометрией четырёхмерного Минковского пространства.

  Принцип относительности был известен (и справедлив) в классической механике, но свойства преобразований движения при u << c и при u ~ c различны; при u << с релятивистские эффекты исчезают и преобразования движения переходят в преобразования инвариантности, справедливые для классической механики (преобразования Галилея; см. Галилея принцип относительности). Поэтому различают релятивистский принцип относительности, обычно называют принципом относительности Эйнштейна, и нерелятивистский принцип относительности Галилея.

  Основное понятие О. т. — точечное событие, т.е. нечто, происходящее в данной точке пространства в данный момент времени (например, световая вспышка, распад элементарной частицы). Это понятие является абстракцией — реальные события всегда имеют некоторую протяжённость в пространстве и во времени и могут рассматриваться как точечные только приближённо. Любой физический процесс есть последовательность событий (С)—C₁, C₂,..., С_п,.... Справедливость симметрий 1—4 означает, что наряду с последовательностью (С) законы природы допускают существование бесконечного числа др. последовательностей (С *), которые получаются из (С) соответствующим преобразованием и различаются положением событий в пространстве и времени, но имеют одинаковую с (С) внутреннюю структуру. Например, в случае симметрии 4 процесс (С) можно наглядно описать как происходящий в стоящем на земле самолёте, а процесс (С *) — как такой же процесс, происходящий в самолёте, летящем с постоянной скоростью (относительно земли); различным скоростям и направлениям движения соответствуют различные последовательности (С *). Преобразования, переводящие одну последовательность событий в другую, называются активными (в отличие от пассивных преобразований, которые связывают координаты одного и того же события в двух системах отсчёта; см. ниже). Совокупность этих преобразований должна удовлетворять определённым свойствам. Прежде всего последовательное применение любых двух преобразований должно представлять собой одно из возможных преобразований [например, переход от системы (1) к системе (2), а затем от системы (2) к системе (3) эквивалентен переходу (1)—(3)]. Кроме того, для каждого преобразования должно существовать обратное преобразование, так что последовательное применение обоих преобразований даёт тождественное (единичное) преобразование, являющееся одним из возможных преобразований системы. Это означает, что совокупность рассматриваемых преобразований (1—4) должна составлять группу в математическом смысле. Эта группа называется группой Пуанкаре (название предложено Ю. Вигнером). Преобразования группы Пуанкаре носят универсальный характер: они действуют одинаково на события любого типа. Это позволяет считать, что они описывают свойства пространства-времени, а не свойства конкретных процессов. Свойства преобразований Пуанкаре могут быть описаны различными способами (так же, как можно описывать различными способами свойства движений в трёхмерном пространстве); наиболее простое описание получается при использовании инерциальных систем отсчёта и связанных с ними часов. Роль инерционных систем отсчёта (и. с. о.) в О. т. такая же, как роль прямоугольных декартовых координат в геометрии Евклида.

  Инерциальные системы отсчёта

  С той степенью точности, с какой свойства данной области пространства-времени описываются частной О. т., можно ввести и. с. о., в которых описание пространственно-временных закономерностей О. т. принимает особенно простую форму. Под системой отсчёта в этом случае можно подразумевать жёсткую систему твёрдых тел (или её мысленное продолжение), по отношению к которой определяются положения событий, траектории тел и световых лучей. Любая система отсчёта, движущаяся относительно данной и. с. о. равномерно и прямолинейно без вращения, также будет инерциальной, а система отсчёта, вращающаяся или движущаяся ускоренно, уже не будет и. с. о. Следовательно, и. с. о. образуют выделенный класс систем отсчёта. В и. с. о. справедлив закон инерции, т. е. свободная (не испытывающая воздействий др. тел) частица движется в и. с. о. прямолинейно и (при принятой синхронизации часов; см. ниже) равномерно. Требование выполнения закона инерции может быть принято как определение и. с. о. Первый закон Ньютона может рассматриваться при этом как утверждение о существовании таких систем отсчёта. Все и. с. о. равноправны; это равноправие является непосредственным выражением принципа относительности.

  Степень инерциальности системы отсчёта зависит от свойств гравитационных полей, действующих в рассматриваемой области пространства-времени. Количественные критерии применимости частной О. т. и инерциальности систем отсчёта рассматриваются в ОТО.

  В области пространства-времени, в которой справедлива частная О. т., можно пользоваться и неинерционными системами отсчёта (так же, как можно пользоваться криволинейными координатами в геометрии Евклида), но при этом описание свойств пространства-времени оказывается более сложным.

  В данной и. с. о. необходимо определить способ измерения времени и координат. В и. с. о. трёхмерная пространственная геометрия — евклидова, если прямые определить, например, как траектории световых лучей, а расстояния измерять твёрдыми масштабами. Поэтому в данной и. с. о. можно ввести декартовы прямоугольные координаты х, у, z. Для определения времени t события можно принять, что в той точке, где оно произошло, находятся часы, покоящиеся в данной и. с. о. Если события происходят в разных точках A, В, то для сравнения их времён нужно синхронизировать часы в A и В, т.е. определить значение того, что часы в А и В показывают одинаковое время. Обычное определение таково: пусть в момент t_A по часам в А посылается сигнал в В, а в момент его прибытия в В посылается такой же сигнал из В в A; если сигнал пришёл в А в момент t’_A, то принимается, что сигнал пришёл в В в момент t_B = (t_A + t ’_A)/2 и соответственно устанавливаются часы в В. При таком определении времена распространения сигнала из A в В и из В в А одинаковы и равны (t ’_A – t_A)/2. Сигналами могут служить световые вспышки, звуковые сигналы (если среда, в которой они распространяются, покоится по отношению к данной системе отсчёта), выстрелы из двух одинаковых орудий, установленных в A и В, и т.д., требуется лишь, чтобы условия передачи сигнала из А в В и из В в А были одинаковыми. Целесообразность такого определения времени связана с тем, что в любой и. с. о. отсутствует какое-либо физически выделенное направление; описанная процедура синхронизации часов симметрична относительно A и В и поэтому не вносит анизотропии в способ описания. Отсутствие выделенного направления проявляется в том, что синхронизация любыми сигналами приводит к одному и тому же результату; к такому же результату приводит медленный (с u << с) перенос часов из A в В. При практических измерениях времён и координат используются многочисленные косвенные методы, при условии, что они дают такой же результат, как и описанные выше процедуры. В любой другой и. с. о. координаты и время измеряются с помощью таких же масштабов и часов, синхронизируемых таким же способом. Заранее не очевидно, что времена, определённые таким образом в двух различных и. с. о., будут одними и теми же, и они действительно оказываются различными. После того как синхронизация произведена, могут измеряться скорости частиц и сигналов в данной и. с. о., в частности скорость распространения световых сигналов. Скорость света в любой и. с. о. всегда равна с.

  Преобразования Лоренца

  Рассмотренные выше активные преобразования непосредственно связаны с пассивными преобразованиями, описывающими связь между координатами и временем данного события в двух различных и. с. о. В силу принципа относительности безразлично, сообщить ли телу скорость V по отношению к данной и. с. о. L или перейти к системе отсчёта L¢, движущейся со скоростью V относительно L, — закон преобразования координат и времени должен быть одним и тем же.

  Вследствие справедливости симметрий 1—4, преобразования, связывающие координаты и времена событий х, у, z, t и х’, у’, z’, t’, измеренные в двух и. с. о. L и L’, должны быть линейными. Из симметрий 1—4 и требования, чтобы преобразования составляли группу, можно получить вид этих преобразований. Если система отсчёта L’ движется относительно L со скоростью V, то при надлежащем выборе осей координат и начал отсчёта времени в L и L’ (оси х и х’ совпадают и направлены по V, оси у и у’, z и z’ соответственно параллельны, начала координат О и О’ совпадают при t = 0 и часы в L’ установлены так, что при t = 0 часы в О’ показывают время t’ = 0) преобразования координат и времени имеют вид:

,  ,  , (2)

  где с – произвольная постоянная, имеющая смысл предельной скорости движения (равной скорости света в вакууме). Эта постоянная может быть определена из любого эффекта О. т. (например, замедления времени распада быстрого p-мезона). Справедливость кинематики и динамики, основанных на преобразованиях (2), подтверждена неисчислимой совокупностью экспериментальных фактов.

  Преобразования Лоренца (2) вместе с преобразованиями вращения вокруг начала координат образуют группу Лоренца; добавление к ней сдвигов во времени t’ = t + а и в пространстве х’ = х + b (где a, b произвольные постоянные размерности времени и длины) даёт группу Пуанкаре.

  Из принципа относительности вытекает, что физические законы должны иметь одинаковую форму во всех и. с. о.; следовательно, они должны сохранять свой вид при преобразованиях Лоренца. Это требование называется принципом (постулатом) релятивистской инвариантности, или лоренц-инвариантности (лоренц-ковариантности), законов природы.

  Из преобразований Лоренца вытекает релятивистский закон сложения скоростей. Если частица или сигнал движется в L по оси х со скоростью u, то в момент tx = ut и скорость частицы u’ = x’ / t’, измеряемая в системе L’, равна:

  (3)

  Эта формула отражает основную черту релятивистской кинематики — независимость скорости света от движения источника. Действительно, если скорость света, испущенного покоящимся в некоторой и. с. о. L источником, есть с, u = с, то из закона сложения скоростей (2) получаем, что измеренная в и. с. о. L’ скорость света u’ также равна с. Так как направление оси х произвольно, то отсюда следует независимость скорости света от движения источника. Это свойство скорости света однозначно определяет вид преобразований Лоренца: постулировав независимость скорости света от движения источника, однородность пространства и времени и изотропию пространства, можно вывести преобразования Лоренца.

  Особая роль скорости света в О. т. связана с тем, что она является предельной скоростью распространения сигналов и движения частиц, достигаемой при энергии частицы, стремящейся к бесконечности, или массе, стремящейся к нулю; если бы масса покоя m_g фотона оказалась хотя и очень малой, но отличной от нуля (экспериментально установлено, что m _g < 4×10^–21m_e, где m_e — масса электрона), то скорость света была бы меньше предельной. Чтобы предельная скорость вообще могла существовать, она не должна зависеть от движения источника частиц.

  Из преобразований Лоренца легко получить основные эффекты О. т.: относительность одновременности, замедление времени, сокращение продольных размеров движущихся тел. Действительно, события 1, 2, одновременные в одной и. с. о. L: t ₁ = t ₂ и происходящие в разных точках x ₁, x ₂, оказываются неодновременными в другой и. с. о. L’ : . Далее, когда часы, покоящиеся в L в точке х = 0, показывают время t, то время t’ по часам в L’, пространственно совпадающим с часами в L в этот момент времени, есть

 (4)

  или

 (4, а)

  т. е. с точки зрения наблюдателя в L’ часы в L отстают. В силу принципа относительности отсюда следует, что с точки зрения наблюдателя в L’, все процессы в L замедлены в такое же число раз.

  Легко получить также, что размеры l всех тел, покоящихся в L, оказываются при измерении в L’ сокращёнными в  раз в направлении V:

 (5)

  В частности, продольный диаметр сферы, движущейся со скоростью u относительно L’, будет при измерении в L¢ в  раз короче, чем поперечный. (Заметим, что это сокращение не обнаружилось бы на мгновенной фотографии сферы: из-за различного запаздывания световых сигналов, приходящих от разных точек сферы, её видимая форма остаётся прежней.)

  Для и. с. о. пространственно-временные эффекты, определяемые преобразованиями Лоренца, относительны: с точки зрения наблюдателя в L замедляются все процессы и сокращаются все продольные масштабы в L’. Однако это утверждение несправедливо, если хотя бы одна из систем отсчёта неинерциальна. Если, например, часы 1 перемещаются относительно L из А в В со скоростью u, а потом из В в А со скоростью — u, то они отстанут по сравнению с покоящимися A часами 2 в  раз; это можно обнаружить прямым сравнением, так что эффект абсолютен. Он должен иметь место для любого процесса; например, близнец, совершивший путешествие со скоростью u, вернётся в  раз более молодым, чем его брат, остававшийся неподвижным в и. с. о. Это явление, получившее название «парадокса близнецов», в действительности не содержит парадокса: система отсчёта, связанная с часами 1, не является инерциальной, т.к. эти часы при повороте в В испытывают ускорение по отношению к инерциальной системе; поэтому часы 1 и 2 неравноправны.

  При малых скоростях u преобразования Лоренца переходят в преобразования Галилея x’ = x – ut, y ’ = y, z’’ = z, t ’ = t, которые описывают связь между картинами различных наблюдателей, известную из повседневного опыта: размеры предметов и длительность процессов одинаковы для всех наблюдателей.

  Преобразования Пуанкаре оставляют инвариантной величину, называемую интервалом s_AB между событиями А, В, которая определяется соотношением:

s²_AB = c²(t_A – t_B)² – (x_A – x_B)² – (y_A – y_B)² – (z_A – z_B)². (6)

  Математически инвариантность s аналогична инвариантности расстояния при преобразованиях движения в евклидовой геометрии. Величины ct, х, у, z можно рассматривать как четыре координаты события в четырёхмерном пространстве Минковского: х ⁰ = ct, х ¹ = х, x ² = у, x ³ = z, которые являются компонентами четырёхмерного вектора.

  Если вместо x ⁰ ввести мнимую координату x ⁴ = ix ⁰ = ict, то произвольное преобразование Пуанкаре можно записать в виде, полностью аналогичном формуле, описывающей вращения и сдвиги в трёхмерном пространстве.

  Вследствие того, что квадраты разностей временных и пространственных координат входят в (6) с разными знаками, знак s ² может быть различным; геометрия такого пространства отличается от евклидовой и называется псевдоевклидовой. В такой геометрии интервалы разделяются на три типа: s ² < 0, s ² > О и s ² = 0. Интервалы первого и второго типа называются соответственно времениподобными и пространственноподобными. Если s ² ³ 0, знак t_A – t_B не зависит от системы отсчёта. Это тесно связано с принципом причинности. Действительно, если s ² ³ 0 и (для определённости) t_A < t_B, то события А и В могут быть связаны сигналом, распространяющимся со скоростью u £ с, т.е. А может быть причиной В. Обычные представления о причинности требуют тогда, чтобы в любой системе отсчёта событие В следовало за событием А. Инвариантность условия s ² = 0 непосредственно выражает инвариантность скорости света. Если s ² < 0, то знак t_A – t_B может быть различным в разных и. с. о. Однако это не противоречит причинности, т.к. такие события не могут быть связаны никаким взаимодействием.

  Если s ² < 0, то существует такая система отсчёта, в которой события А и В одновременны; в этой системе s ² = –l ², где l — обычное расстояние. При s ² > 0 существует система отсчёта, в которой события А и В происходят в одной точке.

  В классической физике требование инвариантности законов физики относительно преобразований Лоренца означает, что любые физические величины должны преобразовываться как скаляры, векторы или тензоры в пространстве Минковского. Правила вычислений с такими величинами даются тензорным исчислением. Использование тензорного исчисления позволяет записывать законы физики в таком виде, что их лоренц-инвариантность становится непосредственно очевидной.

  Законы сохранения в теории относительности и релятивистская механика

  В О. т., так же как в классической механике, для замкнутой физической системы сохраняется импульс р и энергия Е. Трёхмерный вектор импульса вместе с энергией образует четырёхмерный вектор импульса-энергии с компонентами Е /с, р, обозначаемый как (Е /с, р). При преобразованиях Лоренца остаётся инвариантной величина

E ² – (cp) ² = m ²c ⁴, (7)

  где m – масса покоя частицы. Из требований лоренц-инвариантности следует, что зависимость энергии и импульса от скорости имеет вид

, . (8)

  Энергия и импульс частицы связаны соотношением р = Eu/c². Это соотношение справедливо также для частицы с нулевой массой покоя; тогда u = с и р = Е/с. Такими частицами, по-видимому, являются фотоны (g) и электронные и мюонные нейтрино. Из (8) видно, что импульс и энергия частицы с m ¹ 0 стремятся к бесконечности при u ® с.

  Обсуждалась возможность существования объектов, движущихся со скоростью, большей скорости света (т. н. тахионов). Формально это не противоречит лоренц-инвариантности, но приводит к серьёзным затруднениям с выполнением требования причинности.

  Масса покоя т не является сохраняющейся величиной. В частности, в процессах распадов и превращений элементарных частиц сумма энергий и импульсов частиц сохраняется, а сумма масс покоя меняется. Так, в процессе аннигиляции позитрона и электрона е ⁺ + е^– ® 2g сумма масс покоя изменяется на 2 m_е.

  В системе отсчёта, в которой тело покоится (такая система отсчёта наз. собственной), его энергия (энергия покоя) есть Е₀ = mс ². Если тело, оставаясь в покое, изменяет своё состояние, получая энергию в виде излучения или тепла, то из релятивистского закона сохранения энергии следует, что полученная телом энергия DЕ связана с увеличением его массы покоя соотношением DЕ = Dmc ². Из этого соотношения, названного Эйнштейном принципом эквивалентности массы и энергии, следует, что величина Е₀ = mc ² определяет максимальную величину энергии, которая может быть «извлечена» из данного тела в системе отсчёта, в которой оно покоится.

  Для движущегося тела величина

   (9)

определяет его кинетическую энергию. При u << с (9) переходит в нерелятивистское выражение Е_кин = mu ²/2, при этом импульс равен р = mu. Из определения Е_кин следует, что для любого процесса в изолированной системе выполняется равенство:

, (10)

согласно которому увеличение кинетической энергии пропорционально уменьшению суммы масс покоя. Это соотношение широко используется в ядерной физике; оно позволяет предсказывать энерговыделение в ядерных реакциях, если известны массы покоя участвующих в них частиц. Возможность протекания процессов, в которых происходит превращение энергии покоя в кинетическую энергию частиц, ограничена др. законами сохранения (например, законом сохранения барионного заряда, запрещающим процесс превращения протона в позитрон и g-квант).

  Иногда вводят массу, определяемую как

; (11)

  при этом связь между импульсом и энергией имеет тот же вид, что и в ньютоновской механике: р = m_движu. Определённая таким образом масса отличается от энергии тела лишь множителем 1/с ². (В теоретич. физике часто выбирают единицы измерения так, что с = 1, тогда Е = m_движ.)

  Основные уравнения релятивистской механики имеют такой же вид, как второй закон Ньютона и уравнение энергии, только вместо нерелятивистских выражений для энергии и импульса используются выражения (8):

,

, (12)

где F — сила, действующая на тело. Для заряженной частицы, движущейся в электромагнитном поле, F есть Лоренца сила.

  Теория относительности и эксперимент

  Предположения о точечных событиях, справедливости принципа относительности, однородности времени и однородности и изотропии пространства с неизбежностью приводят к О. т. При этом абстрактно допустим предельный случай, соответствующий с = ¥, однако такая возможность исключена экспериментально: доказано с огромной точностью (см. ниже), что предельная скорость с есть скорость света в вакууме (её значение дано в начале статьи).

  Каковы границы применимости О. т.? Отклонения от пространственно-временной геометрии О. т., связанные с гравитацией, наблюдаемы и рассчитываются в ОТО; никаких др. ограничений применимости О. т. пока не обнаружено, хотя неоднократно высказывались подозрения, что на очень малых расстояниях (например, ~10^–17 см) понятие точечного события, а следовательно, и О. т. могут оказаться неприменимыми (см., например, Квантование пространства-времени).

  Предположение о лоренц-инвариантности и точечности событий (означающей локальность взаимодействий) лежит в основе всех современных теорий, в которых существен релятивизм. Справедливость квантовой электродинамики электронов и мюонов, а следовательно, и О. т. установлена вплоть до расстояний 10^–15 см. При энергиях порядка масс этих частиц согласие квантовой электродинамики с опытом установлено с относительной точностью, несколько лучшей, чем 10^–5; с точностью того же порядка должна быть справедлива и механика О. т.

  Релятивистские законы сохранения применяются при исследованиях превращений элементарных частиц, вызванных сильным, слабым и электромагнитным взаимодействиями; отсутствие противоречий подтверждает справедливость этих законов. Всё, что известно о названных взаимодействиях, согласуется с представлением об их лоренц-инвариантности.

  Предположение о невозможности сверхсветовых сигналов, вытекающее из О. т., лежит в основе дисперсионных методов, широко используемых в теории сильных взаимодействий (см. также Квантовая теория поля); их успех демонстрирует справедливость основных представлений О. т.

  Одним из наиболее ярких подтверждений справедливости релятивистской инвариантности явилось предсказание на её основе существования античастиц и их последующее открытие (см. Дирака уравнение, Античастицы).

  Требование лоренц-инвариантности взаимодействий приводит при очень общих предположениях к т. н. СРТ-теореме, устанавливающей связь между свойствами частиц и античастиц. Эта связь выполняется на опыте для всех известных взаимодействий.

  Неоднократно ставились опыты по прямой проверке основных черт кинематики О. т. Независимость скорости света от движения источника проверена с наилучшей точностью в 1964 в опытах [Европейский центр ядерных исследований (ЦЕРН, Швейцария)], в которых использовались g-кванты от распада p°-мезона; при скорости p°u = 0,9997с относит. точность совпадения скорости g-кванта с с составляла 10^–4. Релятивистское замедление времени измерено в широком интервале скоростей с помощью поперечного Доплера эффекта и непосредственно по распадам элементарных частиц с точностью 1–5%. Неоднократно проверялась также формула 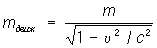; наилучшая достигнутая точность — 5×10^–4 (В. Мейер и др., 1963).

  История частной теории относительности

  Хотя О. т. в логическом смысле проста, путь, приведший к ней, был сложным. Справедливость принципа относительности для механических явлений и его связь с явлением инерции были поняты после появления теории Н. Коперника: отсутствие видимых проявлений движения Земли с неизбежностью приводило к заключению, что общее движение системы не сказывается на происходящих в ней механических явлениях. Уже в 16 в. это поясняли, описывая эксперименты на движущемся корабле. Классическое изложение принципа относительности было дано в 1632 Г. Галилеем: «Заставьте теперь корабль двигаться с любой скоростью и тогда (если только движение будет равномерным и без качки в ту и другую сторону) во всех...явлениях вы не обнаружите ни малейшего изменения и ни по одному из них не сможете установить, движется ли корабль или стоит неподвижно» (Галилей Г., Диалог о двух главнейших системах мира: птоломеевой и коперниковой, М.–Л., 1948, с. 147). Принцип относительности широко использовался Х. Гюйгенсом для решения задач механики.

  Полная система законов движения для любой механической системы была дана И. Ньютоном в «Началах» (1687). Ньютон, установив, что законы механики не могут быть справедливыми в любой системе отсчёта, ввёл понятия абсолютного пространства и абсолютного времени; по существу это были для него система отсчёта и временная переменная t, для которых выполнялись законы движения. Вопрос об измерении времени в механике Ньютона был простым, т.к. любые равномерно движущиеся часы годились для измерения t. Более сложным был вопрос об абсолютном пространстве. В механике Ньютона выполнялся принцип относительности. Согласно формулировке Ньютона, «относительные движения друг по отношению к другу тел, заключённых в каком-либо пространстве, одинаковы, покоится ли это пространство или движется равномерно и прямолинейно без вращения» («Математические начала натуральной философии», см. Крылов А. И., Собрание трудов, т. 7, 1936, с. 49). Поэтому нельзя было отличить покоящуюся в абсолютном пространстве систему отсчёта от равномерно движущейся. Переход от одной и. с. о. к другой в механике Ньютона описывался преобразованиями x ’ = х – ut, t ’ = t, называется сейчас преобразованиями Галилея. Такая форма преобразований казалась очевидной, т.к. не сомневались в том, что длины предметов должны быть одинаковыми в любой системе отсчёта, а время единым. Эта уверенность подтверждалась инвариантностью законов Ньютона относительно преобразований Галилея. Столь же несомненным казалось то, что для оптических явлений принцип относительности несправедлив. Уже в 17 в. широко использовалось представление о заполняющей пространство среде — эфире. Среди многих функций, приписывавшихся эфиру, была передача световых возмущений. В начале 19 в. была разработана оптика Т. Юнга — О. Френеля, в которой скорость света относительно эфира считалась константой, не зависящей от движения источника. Отсюда следовало нарушение принципа относительности, т.к. для наблюдателя, движущегося в эфире со скоростью u навстречу световому лучу, скорость света должна была бы равняться с + u (эфирный ветер). Такой эфирный ветер должен был бы возникать, в частности, из-за орбитального движения Земли (со скоростью 30 км/сек). Поиски эфирного ветра затруднялись, однако, тем, что уже по теории Френеля эффекты порядка u /c (~10^–4 для орбитального движения Земли) должны отсутствовать в широком классе опытов.

  Проблема эфира заняла одно из центр. мест в физике после построения Дж. Максвеллом теории электромагнитного поля, в которой эфир стал носителем не только световых волн, но и электрических и магнитных полей. Попытки обнаружения эфирного ветра были сделаны А. Майкельсоном (1881) и А. Майкельсоном и Э. Морли (1887), искавшими эффект порядка u²/c², и дали отрицательный результат (см. Майкельсона опыт). Возникла проблема согласования опыта Майкельсона с оптикой и электродинамикой, основанными на представлении об эфире. Наиболее очевидными казались объяснения, базирующиеся на гипотезе полного увлечения эфира движущимися телами. Оптические и электромагнитные теории, использовавшие эту гипотезу, обсуждались (Дж. Г. Стокс, Г. Герц), но они оказались либо внутренне противоречивыми, либо не описывали всей совокупности экспериментальных фактов. Наиболее успешной была электродинамика Х. Лоренца, в основе которой лежало представление о неподвижном эфире и которая, на первый взгляд, была несовместима с принципом относительности. В 1892 Лоренц (ранее английский физик Дж. Фицджеральд, 1889) заметил, что отрицательный результат опыта Майкельсона объясняется, если продольные размеры всех тел сокращаются в  раз при движении тел относительно эфира со скоростью u. Это сокращение (т. н. Лоренца – Фицджеральда сокращение) Лоренц объяснял изменением действующих в телах электромагнитных сил при движении тела через эфир. В 1895 Лоренц, рассматривая соответствие между движущейся и неподвижной относительно эфира системами тел, ввёл (в приближении u /c) понятие «местного времени» t’ = t – (u /c)(x – ut) и доказал, что эффекты движения относительно эфира отсутствуют в порядке u /c.

  Ситуация наталкивала на мысль о необнаружимости движения относительно эфира. Такой вывод сделал А. Пуанкаре, который начиная с 1895 выражал убеждение, что движение относительно эфира необнаружимо принципиально. В 1900-е гг. при обсуждении электромагнитных явлений он начал пользоваться термином «принцип относительности», формулируя его как невозможность обнаружения движения относительно эфира. В начале 1900-х гг. был проведён ряд опытов, подтвердивших, что движение Земли не влияет на электромагнитные, в частности на оптические, явления. [К этому вопросу возвращались и после создания О. т.; в 1963, например, отсутствие эфирного ветра проверено в опытах, которые могли бы обнаружить эфирный ветер в несколько м /сек (Д. Чампней и др.).] Проблема согласования этого факта с электродинамикой Максвелла — Лоренца стала насущной.

  Объяснение невозможности обнаружить абсолютное движение в рамках представлений об эфире и связанной с ним привилегированной системе отсчёта было дано Лоренцом и Пуанкаре в 1904—05. Предполагая, что уравнения электродинамики Лоренца (см. Лоренца — Максвелла уравнения) справедливы в системе координат, покоящейся относительно эфира, они сделали вывод, что все тела при движении в эфире испытывают лоренц-фицджеральдовское сжатие, а происходящие в них движения изменяются определённым образом, но эти изменения в силу их универсальности необнаружимы для наблюдателя, движущегося вместе с телом. Преобразования, названные Пуанкаре преобразованиями Лоренца, описывали связь между пространственно-временными координатами для процессов в двух телах, одно из которых двигалось, а другое покоилось относительно эфира. (Ранее близкие преобразования применил нем. физик В. Фохт; правильные преобразования нашёл впервые Дж. Лармор в 1900.)

  В завершающей работе Пуанкаре (поступившей в печать 23 июля 1905) содержался разработанный математический анализ релятивистских преобразований, интерпретировавшихся в описанном выше смысле. Было показано, что преобразования Лоренца образуют группу, оставляющую инвариантным интервал x ² + y ² + z ² – c ²t ²; были найдены преобразования для потенциалов электромагнитного поля, плотностей тока и заряда, установлена инвариантность действия для электромагнитного поля, показано, что группа Лоренца является группой инвариантности уравнений электродинамики. Лоренц и Пуанкаре видели также универсальный характер лоренц-инвариантности, которую они формулировали как требование, чтобы все силы и массы преобразовывались так же, как электромагнитные.

  Ещё в 1904 Пуанкаре, перечисляя принципы классической физики, дал общую и полную формулировку принципа относительности: «Законы природы должны быть одинаковы как для неподвижного наблюдателя, так и для наблюдателя, находящегося в состоянии равномерного и прямолинейного движения, так что не существует и не может существовать способа обнаружить, находимся мы в состоянии такого движения или нет» («Bulletin des sciences mathématiques», 1904, v. 25, sér. 2, p. 302).

  Для того чтобы убедиться, что постулат относительности в такой форме выполним, был необходим последовательный анализ измерения пространственно-временных координат в произвольной и. с. о. Важный шаг в этом направлении был сделан Пуанкаре ещё в 1900, когда он заметил, что синхронизация часов светом в системе отсчёта, движущейся относительно эфира, даёт местное время Лоренца в приближении u /c. Последовательно такой анализ уже с современной точки зрения был сделан Эйнштейном.

  В работе, направленной в печать 30 июня 1905, Эйнштейн изложил совершенно новую точку зрения на проблему принципа относительности. Он сделал вывод, что из невозможности обнаружить абсолютное движение следует равноправие всех и. с. о. Эйнштейн отказался от представления об эфире и стал рассматривать поле в пустоте как новый вид физического объекта, не нуждающийся в механическом носителе (эфире). Это было революционным шагом, означавшим резкий разрыв с господствовавшими в физике того времени взглядами. Равноправие всех и. с. о. логически требовало признания полного равноправия пространственно-временных координат, измеряемых в любой и. с. о. Эйнштейн дал последовательный анализ физического содержания понятий времени и координат события, исходя из того, что координаты в каждой и. с. о. измеряются стандартными масштабами, а время — часами, синхронизированными светом, и поставил и разрешил вопрос о связи пространственных и временных координат, измеренных в разных и. с. о. Эта связь должна была быть такой, чтобы электродинамика Максвелла — Лоренца, находившаяся в согласии с обширной совокупностью фактов, была справедлива в любой и. с. о. Из уравнений Максвелла — Лоренца вытекает, что скорость света в вакууме не зависит ни от направления распространения света, ни от движения источника. Т. о., в них неявно содержались и принятая Эйнштейном синхронизация часов светом и универсальное постоянство скорости света. Дав явное определение синхронизации часов и сформулировав 2 постулата —

  «1. Законы, по которым изменяются состояния физических систем, не зависят от того, к которой из двух координатных систем, движущихся относительно друг друга равномерно и прямолинейно, эти изменения состояния относятся.

  2. Каждый луч света движется в «покоящейся» системе координат с определённой скоростью V, независимо от того, испускается ли этот луч света покоящимся или движущимся телом» (Собр. научных трудов, т. 1, М., 1965, с. 10), — из которых следовала независимость скорости света от движения источника для любой и. с. о., Эйнштейн нашёл связь между пространственно-временными координатами события, измеряемыми в различных и. с. о. Полученные преобразования, математически тождественные преобразованиям Лоренца, приобрели, т. о., в работе Эйнштейна новое физическое содержание, а требование лоренц-инварнантности законов природы стало очевидным следствием и выражением равноправия всех и. с. о.

  Анализ содержания релятивистских преобразований привёл Эйнштейна к заключению о необходимости изменения складывавшихся в течение столетий представлений об абсолютности длины, времени и одновременности; отказ от них позволил установить относительный характер сжатия Лоренца — Фицджеральда и др. явлений, рассматривавшихся ранее как «реальные» эффекты, вызванные движением тела относительно эфира.

  Т. о., Эйнштейном было дано полное решение проблемы относительности и построена О. т. как физическая теория пространства-времени, основанная на представлении об относительном характере релятивистских явлений и относительности времени. Найденное Эйнштейном объединение принципа относительности с относительностью одновременности получило название «принцип относительности Эйнштейна».

  Открытие относительности одновременности было завершением развития идеи относительности, в начале которого стояла теория Н. Коперника. Из теории Коперника следовала относительность «места в пространстве»; Эйнштейн сделал аналогичный вывод для понятия «момента времени». Вместо них основным понятием теории стало понятие события — оно абсолютно в том смысле, что два совпадающих события остаются таковыми для любого наблюдателя.

  В 1905—06 Эйнштейн, применив принцип относительности, установил связь между массой и энергией, а вскоре М. Планк (1906) нашёл релятивистские выражения для энергии и импульса электрона, не прибегая к гипотезам о его структуре (использовавшимся ранее в работах Лоренца и Пуанкаре), и тем самым завершил программу «релятивизации» классической электродинамики. В 1906 Планк ввёл термин «теория относительности». В 1907—08 Г. Минковский указал, что О. т. может рассматриваться как геометрия пространства-времени; в его работах был развит современный четырёхмерный аппарат теории. К 1910 построение О. т. в основном завершается, но её воздействие на развитие теоретической физики только начинается.

  Появление теории относительности Эйнштейна оказало существ, влияние на развитие революции в физике, происходившей в начале 20 в. О. т. была первой физической теорией, продемонстрировавшей, что представления, основанные на повседневном опыте, казавшиеся очевидными и отождествлявшиеся с истинами «здравого смысла», могут оказываться неприменимыми при переходе в новые области опыта. О. т. стала первой «не наглядной» научной теорией. Революционизировав мышление физиков, О. т. подготовила почву для ещё более далеко идущего отказа от «непосредственно очевидных» представлений, потребовавшегося для создания квантовой механики.

  О. т. оказала большое непосредственное воздействие на всё последующее развитие физики. Так, успех релятивистской кинематики при объяснении Комптона эффекта стал одним из центральных аргументов в пользу корпускулярной природы фотона (1922); использование преобразований Лоренца привело Л. де Бройля (1924) к соотношению l = h /p (где l — длина волны, связанной с движущейся частицей, h — Планка постоянная; см. Волны де Бройля); релятивистская инвариантность послужила ключом к открытию Клейна — Гордона уравнения (1926) и Дирака уравнения (1928). Принцип релятивистской инвариантности сыграл решающую роль в развитии квантовой теории поля; с ним связаны такие её достижения, как установление связи между спином и статистикой (В. Паули, 1940) и создание метода перенормировок в квантовой электродинамике (1949). В современной физике принцип релятивистской инвариантности продолжает играть решающую роль.

  Лит.: Классические труды: Принцип относительности, М. — Л., 1935; Эйнштейн А., Собр. науч. трудов, т. 1—4, М., 1965—67. Учебники и монографии: Паули В., Теория относительности, пер. с англ., М. — Л.,1947; Ландау Л. Д., Лифшиц Е. М., Теория поля, 6 изд., М., 1973 (Теоретическая физика, т. 2); Мандельштам Л. И., Лекции по оптике, теории относительности и квантовой механике, М., 1972; Тейлор Э. Ф., Уилер Д ж. А., Физика пространства-времени, пер. с англ., М., 1969; Угаров В. А., Специальная теория относительности, М., 1968: Фейнман P., Лейтон P., Сэндс М., Фейнмановские лекции по физике, [пер. с англ.], в. 2, М., 1965; Фок В. А., Теория пространства, времени и тяготения, 2 изд., М., 1961. Популярная литература: Борн М., Эйнштейновская теория относительности, пер. с англ., М., 1964; Ландау Л. Д., Румер Ю. Б., Что такое теория относительности, К., 1965; Фейнман Р. П., Характер физических законов, пер. с англ., М., 1968. Обзоры: Вайскопф В., Видимая форма быстродвижущихся тел, «Успехи физических наук», 1964, т. 84, в. 1, с. 183; Блохинцев Д. И., Обоснованность специальной теории относительности опытами в области физики высоких энергий, там же, 1966, т. 89, в. 2, с. 185—99; Шмидт-Отт В. Д., Некоторые новые измерения в связи с доказательством справедливости специальной теории относительности, там же, 1968, т. 96, в. 3, с. 519—27. История: Вавилов С. И., Экспериментальные основания теории относительности, М. — Л., 1928; Лауэ М., История физики, пер. с нем., М., 1956; Франкфурт У. И., Френк А. М., Оптика движущихся тел, М., 1972.

  И. Ю. Кобзарев.