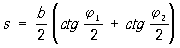 .
.Полигонометрия (от греч. polýgonos — многоугольный и ...метрия) — один из методов определения взаимного положения точек земной поверхности для построения опорной геодезической сети, служащей основой топографических съёмок, планировки и строительства городов, перенесения проектов инженерных сооружений в натуру и т.п. Положения пунктов в принятой системе координат определяют методом П. путём измерения на местности длин линий, последовательно соединяющих эти пункты и образующих полигонометрический ход, и горизонтальных углов между ними. Так, выбрав на местности точки 1, 2, 3, …, n, n + 1 измеряют длины s1, s2,..., sn. Линий между ними и углы b2, b3,..., bn между этими линиями (рис. 1).
Как правило, начальную точку 1 полигонометрического хода совмещают с опорным пунктом Рн, который уже имеет известные координаты хн, ун и в котором известен также исходный дирекционный угол aн направления на какую-нибудь смежную точку Р'н. В начальной точке полигонометрического хода, т. е. в пункте Рн, измеряют также примычный угол b1 между первой стороной хода и исходным направлением РнР’н. Тогда дирекционный угол ai стороны i и координаты xi+1, yi+1 пункта i + 1 полигонометрического хода могут быть вычислены по формулам:
ai = aн + åir=1br - i 180°
xi+1 = хн + åir=1srcosar
yi+1 = ун + åir=1srsinar.
Для контроля и оценки точности измерений в полигонометрическом ходе его конечную точку n + 1 совмещают с опорным же пунктом Pk, координаты xk, yk которого известны и в котором известен также дирекционный угол ak направления на смежную точку P'k. Это даёт возможность вычислить т. н. угловую и координатные невязки в полигонометрическом ходе, зависящие от погрешностей измерения длин линий и углов и выражающиеся формулами:
fa = an+1 - ak,
fx = xn+1 - xk,
fy = yn+1 - yk.
Эти невязки устраняют путём исправления измеренных углов и длин сторон поправками, которые определяют из уравнительных вычислений по способу наименьших квадратов.
При значительных размерах территории, на которой должна быть создана опорная геодезическая сеть, прокладываются взаимно пересекающиеся полигонометрические ходы, образующие полигонометрическую сеть (рис. 2).
Пункты П. закрепляются на местности закладкой подземных бетонных монолитов или металлических труб с якорями (см. Центр геодезический) и установкой наземных знаков в виде деревянных или металлических пирамид (см. Сигнал геодезический).
Углы в П. измеряют теодолитами, причём объектами визирования, как правило, служат специальные марки, устанавливаемые на наблюдаемых пунктах. Длины сторон полигонометрических ходов и сетей измеряют стальными или инварными мерными лентами или проволоками (см. Базисный прибор). Результаты измерений длин и углов в П. путём введения в них соответствующих поправок приводят в ту систему координат, в которой должны быть определены положения полигонометрических пунктов.
В тех случаях, когда условия местности неблагоприятны для непосредственного измерения линий, длины сторон полигонометрических ходов и сетей определяют косвенно параллактическим методом (т. н. параллактическая полигонометрия). В этом случае для определения длины линии IK посредине её и перпендикулярно и симметрично к ней измеряют короткий базис АВ длиной b, а также на концах линии измеряют параллактические углы j1 и j2 (рис. 3), величины которых обычно бывают около 3—6°. Тогда длину линии IK вычисляют по формуле:
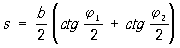 .
.
В зависимости от условий местности применяют и другие схемы косвенного измерения сторон полигонометрических ходов.
В зависимости от точности и очерёдности построения ходы и сети П. делятся на классы, которые должны соответствовать классам триангуляции. Различные классы государственные полигонометрические сети характеризуются следующими показателями точности:
| Классы | Ошибка угла | Ошибка стороны |
| 1 | ± 0,4 | + 1: 300 000 |
| 2 | ± 1,0 | ± 1: 250 000 |
| 3 | ± 1,5 | + 1: 200 000 |
| 4 | ± 2,0 | ± 1: 150 000 |
Полигонометрические сети, создаваемые для инженерных и других целей, особенно для городских съёмок, могут иметь несколько иные показатели точности.
Время возникновения метода П. неизвестно. В прошлом он имел ограниченное применение из-за большого объёма линейных измерений, затруднённых к тому же условиями местности, громоздкости необходимого оборудования и невозможности контроля результатов работы до её полного завершения. Поэтому в прошлом метод П. применялся только для обоснования городских съёмок и для сгущения опорной геодезической сети, созданной методом триангуляции.
Появление в начале 20 в. подвесных мерных приборов из инвара облегчило линейные измерения, повысило их точность и сделало их менее зависимыми от условий местности. В связи с этим метод П. по значению и точности стал сравним с методом триангуляции. Важную роль в развитии П. сыграли исследования русского геодезиста В. В. Данилова, детально разработавшего метод параллактической полигонометрии, который был намечен В. Я. Струве ещё в 1836. С изобретением же электрооптических дальномеров и радиодальномеров, позволяющих непосредственно измерять линии на местности с высокой точностью, метод П. освободился от своего основного недостатка и стал применяться наравне с методом триангуляции. В развитии теорий и методов П. большое значение имели труды советских геодезистов А. С. Чеботарева и В. В. Попова, разработавших рациональные методы ведения полигонометрических работ различного вида и точности, а также методы вычислительной обработки и оценки погрешности их результатов.
Лит.: Справочник геодезиста, под ред. В. Д. Большакова и Г. П. Левчука, М., 1966; Данилов В. В., Точная полигонометрия, 2 изд., М., 1953; Красовский Ф. Н. и Данилов В. В., Руководство по высшей геодезии, ч. 1, в. 2, М., 1939; Чеботарев А. С., Селиханович В. Г., Соколов М. Н., Геодезия, ч. 2, М., 1962; Чеботарев А. С., Уравнительные вычисления при полигонометрических работах, М. — Л., 1934; Попов В. В., Уравновешивание полигонов, 9 изд., М., 1958; Кузин Н. А. и Лебедев Н. Н., Практическое руководство по городской и инженерной полигонометрии, 2 изд., М., 1954; Инструкция о построении государственной геодезической сети СССР, 2 изд., М., 1966.
А. А. Изотов.
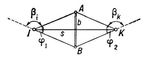
Рис. 3. Определение длины стороны полигонометрического хода параллактическим методом.
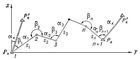
Рис. 1. Полигонометрический ход.
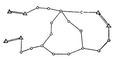
Рис. 2. Полигонометрическая сеть.