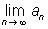 , если он существует, является корнем уравнения (1), а числа a0, a1, a2,..., an,... — приближёнными значениями этого корня. Предел а будет существовать, например, если
, если он существует, является корнем уравнения (1), а числа a0, a1, a2,..., an,... — приближёнными значениями этого корня. Предел а будет существовать, например, еслиПоследовательных приближении метод, метод решения математических задач при помощи такой последовательности приближении, которая сходится к решению и строится рекуррентно (т. е. каждое новое приближение вычисляют, исходя из предыдущего; начальное приближение выбирается в достаточной степени произвольно). П. п. м. применяется для приближённого нахождения корней алгебраических и трансцендентных уравнений, для доказательства существования решения и приближённого нахождения решений дифференциальных, интегральных и интегро-дифференциальных уравнений, для качественной характеристики решения и в ряде др. математических задач. 1) Для решения уравнения
f (x) = 0 (1)
составляют ему равносильное х = j(х), обозначив, например, через j(x) разность х — kf (x) (k — постоянное). Выбрав a0 — начальное приближение к корню уравнения, составляют последовательность чисел a0, a1 = j(a0), a2 = j(a1), …, an = j(an-1), …; предел а = 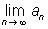 , если он существует, является корнем уравнения (1), а числа a0, a1, a2,..., an,... — приближёнными значениями этого корня. Предел а будет существовать, например, если
, если он существует, является корнем уравнения (1), а числа a0, a1, a2,..., an,... — приближёнными значениями этого корня. Предел а будет существовать, например, если
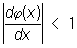 (2)
(2)
и в качестве начального приближения a0 взято любое число.
Обычно, когда надо найти приближённое значение корня уравнения, устанавливают достаточно узкий интервал, в котором лежит корень (например, с помощью графических методов); затем подбирают k так, чтобы условие (2) выполнялось на всём интервале; за начальное приближение a0 выбирают любое число из этого интервала и применяют П. п. м. Практически, после того как два последовательных приближения an-1 и an совпадут с заданной степенью точности, вычисление прекращают и полагают an » а. Пусть дано, например, уравнение f (x) = 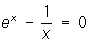 . Так как
. Так как 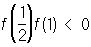 , то корень уравнения лежит в интервале
, то корень уравнения лежит в интервале 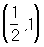 . Положив
. Положив 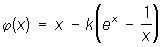 , непосредственной проверкой убеждаемся, что для k =
, непосредственной проверкой убеждаемся, что для k = 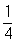 условие (2) выполняется на всём интервале
условие (2) выполняется на всём интервале 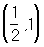 . Выбирем a0 =
. Выбирем a0 = 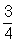 и применим П. п. м. к уравнению
и применим П. п. м. к уравнению 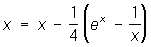 . Получим a1 = 0,554, a2 = 0,570, a3 = 0,566 (на самом деле корень уравнения с тремя верными десятичными знаками равен a4 » 0,567).
. Получим a1 = 0,554, a2 = 0,570, a3 = 0,566 (на самом деле корень уравнения с тремя верными десятичными знаками равен a4 » 0,567).
2) П. п. м. применяют для приближённого решения систем линейных алгебраических уравнений с большим числом неизвестных.
Пусть дана система трёх уравнений с тремя неизвестными:
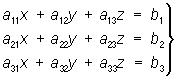 (3)
(3)
Строят ей эквивалентную систему:
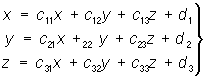 (4)
(4)
полагая, например,
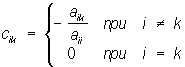
и, пользуясь рекуррентными формулами:
xj = c11xj-1 + c12yj-1 + c13zj-1 + d1
yj = c21xj-1 + c22yj-1 + c23zj-1 + d2
zj = c31xj-1 + c32yj-1 + c33zj-1 + d3
составляют последовательность (x0, у0, z0), (x1, у1, z1),..., (xn, yn, zn),... Если xn ® a, yn ® b, zn ® g при неограниченном увеличении n, то тройка чисел х = a, у = b, z = g будет решением системы (3). Пределы a, b, g заведомо существуют, каковы бы ни были начальные приближения x0, у0, z0, если, например, в каждом уравнении системы (4) сумма абсолютных величин коэффициентов cij меньше единицы.
3) Для того чтобы найти решение у = у (х) дифференциального уравнения 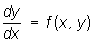 , удовлетворяющее условию у0 = у (х0), записывают это уравнение в виде
, удовлетворяющее условию у0 = у (х0), записывают это уравнение в виде
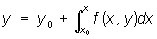
и, пользуясь рекуррентной формулой
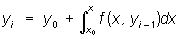
составляют последовательность функций y1(x), у2(х),..., yn (x),... Если она равномерно сходится, то предел её будет искомым решением.
4) Чтобы найти решение первой краевой задачи для уравнения
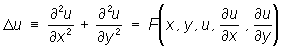
выбирают произвольную дважды дифференцируемую функцию u0(x, у) и составляют затем линейное уравнение
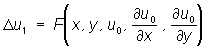 .
.
Пусть u1 (х, у) — решение первой краевой задачи для уравнения (5); считая u1 первым приближением, составляют уравнения типа (5) для последующих приближений. Полученная последовательность {un (x, у)} при некоторых предположениях сходится и даёт решение задачи.
О применимости П. п. м. см. статью Сжатых отображений принцип.