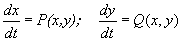
Предельный цикл системы дифференциальный уравнений 2-го порядка

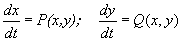
 — замкнутая траектория в фазовом пространстве xOy, обладающая тем свойством, что все траектории, начинающиеся в достаточно узкой кольцеобразной ее окрестности, неограниченно приближаются к этой траектории или при t ® +¥ (устойчивый П. ц.), или при t ® -¥ (неустойчивый П. ц.), или часть из них при t ® +¥, а остальные — при t ® -¥ (полуустойчивый П. ц.). Например, система

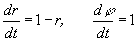
(r и j — полярные координаты), общее решение которой r = 1 – (1 – r₀)e^-t, j = j₀ + t (где r₀ ³ 0), имеет устойчивый П. ц. r = 1 (см. рис.). Понятие П. ц. переносится также на систему n-го порядка. С механической точки зрения устойчивый П. ц. соответствует устойчивому периодическому режиму системы. Поэтому разыскание П. ц. имеет важное значение в теории нелинейных колебаний.

  Лит.: Понтрягин Л. С., Обыкновенные дифференциальные уравнения, 3 изд., М., 1970; Андронов А. А., Витт А. А., Хайкин С. Э., Теория колебаний, 2 изд., М., 1959.

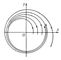
Рис. к ст. Предельный цикл.