Соприкосновение кривой q с кривой / в данной точке М, геометрическое понятие, означающее, что q имеет с l в точке М касание максимального порядка по сравнению с любой кривой из некоторого заранее данного семейства кривых {q}, включающего q. Порядок касания кривых q и / считается равным п, если отрезок QL есть величина n + 1 порядка малости по отношению к отрезку МК (см. рис., где отрезок QL перпендикулярен к общей касательной кривых q и / в точке М). Таким образом, среди всех кривых семейства {q} С. с кривой / имеет та кривая, которая наиболее тесно прилегает к l (для неё отрезок QL имеет максимальный порядок малости). Кривая семейства {q}, которая имеет С. с кривой l в данной её точке М, называется соприкасающейся кривой данного семейства в указанной точке кривой /. Например, соприкасающейся окружностью в точке М кривой / является окружность, которая в этой точке имеет с / максимальный порядок касания по сравнению с любой другой окружностью.
Аналогично вышеизложенному определяется понятие соприкосновения поверхности q, принадлежащей данному семейству поверхностей {q}, с какой-нибудь кривой / (или с поверхностью) в некоторой её точке М (в этих случаях порядок касания определяется также аналогично предыдущему; следует только вместо касательной прямой МК, изображенной на рисунке, рассматривать касательную плоскость поверхности q в точке М). См. Соприкасающаяся плоскость, Соприкасающаяся сфера.
Лит.: Ла Валле-Пуссен Ш. Ж., Курс анализа бесконечно малых, пер. с франц., т. 2, Л. — М., 1933: Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., ч. 1, М., 1971.
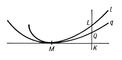
Рис. к ст. Соприкосновение.