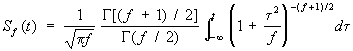Стьюдента распределение с f степенями свободы, распределение отношения Т = X/Y независимых случайных величин Х и Y, где Х подчиняется нормальному распределению  с математическим ожиданием EX = 0 и дисперсией DX = 1, а fY² имеет «Хи-квадрат» распределение с f степенями свободы. Функция распределения Стьюдента выражается интегралом

  .

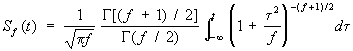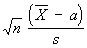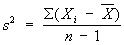Если X₁,..., X_n — независимые случайные величины, одинаково нормально распределённые, причём EX_i = a и DX_i= s² (i = 1,..., n), то при любых действительных значениях а и s > 0 отношение подчиняется С. р. с f = п-1 степенями свободы (здесь  и ). Это свойство было впервые (1908) использовано для решения важной задачи классической теории ошибок У. Госсетом (Англия), писавшим под псевдонимом Стьюдент (Student). Суть этой задачи заключается в проверке гипотезы а = a₀ (a₀ = заданное число, дисперсия s² предполагается неизвестной). Гипотезу а =a₀ считают не противоречащей результатам наблюдений X₁,..., X_n, если справедливо неравенство , в противном случае гипотеза а = а₀ отвергается (так называемый критерий Стьюдента). Критическое значение t = t_n-1(a) представляет собой решение уравнения S_n-1(t) = 1 –,a — заданный значимости уровень (0 < a < 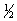). Если проверяемая гипотеза а = а₀ верна, то критерий Стьюдента, соответствующий критическому значению t_n–1(a), может её ошибочно отвергнуть с вероятностью а.

  С. р. используется для решения множества др. задач математической статистики (см. Малые выборки, Ошибок теория, Наименьших квадратов метод).

  Лит.: Крамер Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975.