Суммирование расходящихся рядов и интегралов, построение обобщённой суммы ряда (соответственно значения интеграла), не имеющего обычной суммы (соответственно значения). Расходящиеся ряды могут получаться при перемножении условно сходящихся рядов, при разложении функций в ряд Фурье, при дифференцировании и интегрировании функциональных рядов и т. д. Часто встречаются расходящиеся ряды и интегралы в теории электромагнитного поля и др. вопросах современной физики. Во многих случаях расходящиеся ряды и интегралы можно просуммировать, то есть найти для них сумму (значение) в обобщённом смысле, обладающую некоторыми из основных свойств обычной суммы (значения) сходящегося ряда (интеграла). Обычно требуется, чтобы из того, что ряд 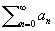 суммируется к S, а ряд
суммируется к S, а ряд 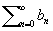 суммируется к Т, следовало, что ряд
суммируется к Т, следовало, что ряд 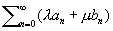 суммируется к lS + lT, а ряд
суммируется к lS + lT, а ряд 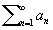 суммируется к S — ао. Кроме того, чаще всего рассматриваются регулярные методы С., то есть методы, суммирующие каждый сходящийся ряд к его обычной сумме. В большинстве методов С. расходящийся ряд рассматривается в известном смысле как предел сходящегося ряда. А именно, каждый член ряда
суммируется к S — ао. Кроме того, чаще всего рассматриваются регулярные методы С., то есть методы, суммирующие каждый сходящийся ряд к его обычной сумме. В большинстве методов С. расходящийся ряд рассматривается в известном смысле как предел сходящегося ряда. А именно, каждый член ряда
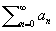 (1)
(1)
умножается на некоторый множитель ln (t) так, чтобы после умножения получился сходящийся ряд
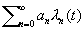 (2)
(2)
с суммой d(t). При этом множители ln (t) выбираются так, чтобы при каждом фиксированном n предел ln (t) при некотором непрерывном или дискретном изменении параметра t равнялся 1. Тогда члены ряда (2) стремятся к соответствующим членам ряда (1). Если при этом d(t) имеет предел, то его называют обобщённой суммой данного ряда, соответствующей данному выбору множителей (данному методу С.). Например, если положить ln (t) = 1 При n £ t и ln (t) = 0 при n > t и брать t ® ¥, то получится обычное понятие суммы ряда; при ln (t) = tn для t < 1 и t ® 1 получается метод Абеля — Пуассона. Часто указывается не результат умножения членов ряда на ln (t), а соответствующие изменения частичных сумм ряда. Например, в методе средних арифметических Чезаро полагают
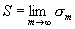 ,
,
где
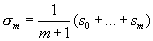 ,
, 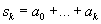 .
.
Этот метод соответствует выбору ln (m) = (m - n + 1)/(m + 1) при n £ m и ln (m) = 0 при n > m. Если положить
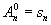 ,
, 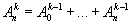 ,
,
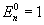 ,
, 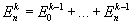 ,
,
и если существует 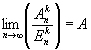 , то говорят, что ряд суммируется к А методом Чезаро k-го порядка. С ростом k возрастает сила метода Чезаро, то есть расширяется множество рядов, суммируемых этим методом. Всякий ряд, суммируемый методом Чезаро какого-либо порядка, суммируется и методом Абеля — Пуассона и притом к той же сумме. Например, ряд 1— 1 + 1 —... + (—1) n-1 +... суммируется методом Абеля — Пуассона к значению 1/2, так как
, то говорят, что ряд суммируется к А методом Чезаро k-го порядка. С ростом k возрастает сила метода Чезаро, то есть расширяется множество рядов, суммируемых этим методом. Всякий ряд, суммируемый методом Чезаро какого-либо порядка, суммируется и методом Абеля — Пуассона и притом к той же сумме. Например, ряд 1— 1 + 1 —... + (—1) n-1 +... суммируется методом Абеля — Пуассона к значению 1/2, так как
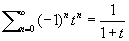 ,
, 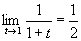 .
.
Метод Чезаро даёт то же значение, так как
s2n= 1, s2n+l = 0, s2n = (n + 1)/(2n + 1),
s2n+1 = 1/2, 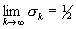 .
.
Методы Чезаро и Абеля — Пуассона применяются в теории тригонометрических рядов для нахождения функции по её ряду Фурье, так как ряд Фурье любой непрерывной функции суммируется к этой функции методом Чезаро первого порядка, а тем самым и методом Абеля — Пуассона. В 1901 Г. Ф. Вороной предложил метод С., частными случаями которого являются все методы Чезаро. Пусть pn ³ 0, p0= 0, 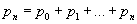 ; обобщённой суммой ряда, по Вороному, называется предел
; обобщённой суммой ряда, по Вороному, называется предел
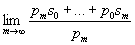 .
.
Метод Вороного регулярен, если
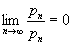 .
.
В 1911 немецкий математик О. Теплиц нашёл необходимые и достаточные условия, которым должна удовлетворять треугольная матрица ||атn|| (где атn = 0 при n > m) для того, чтобы метод С., определяемый формулой 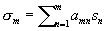 ,
, 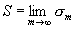 был регулярен. Польский математик Х. Штейнхауз обобщил эти условия на случай квадратных матриц.
был регулярен. Польский математик Х. Штейнхауз обобщил эти условия на случай квадратных матриц.
В теории аналитических функций важную роль играет метод суммирования Бореля, позволяющий аналитически продолжить функцию, заданную степенным рядом, за границу круга сходимости. Важный метод С. тригонометрических рядов был предложен С. Н. Бернштейном и немецким математиком В. Рогозинским. Бернштейн использовал этот метод для получения сходящихся интерполяционных процессов.
Теория С. расходящихся интегралов аналогична теории С. расходящихся рядов. Например, если интеграл

расходится и существует предел
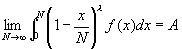 ,
,
то говорят, что первый интеграл суммируем к А методом Чезаро порядка l.
Лит.: Харди Г., Расходящиеся ряды, пер. с англ., М., 1951; Зигмунд А., Тригонометрические ряды, пер. с англ., [2 изд.], т. 1—2, М., 1965; Титчмарт Е., Введение в теорию интегралов Фурье, пер. с англ., М.— Л., 1948; Вари Н. К., Тригонометрические ряды, М., 1961.
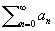 суммируется к S, а ряд
суммируется к S, а ряд 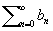 суммируется к Т, следовало, что ряд
суммируется к Т, следовало, что ряд 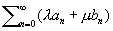 суммируется к lS + lT, а ряд
суммируется к lS + lT, а ряд 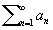 суммируется к S — ао. Кроме того, чаще всего рассматриваются регулярные методы С., то есть методы, суммирующие каждый сходящийся ряд к его обычной сумме. В большинстве методов С. расходящийся ряд рассматривается в известном смысле как предел сходящегося ряда. А именно, каждый член ряда
суммируется к S — ао. Кроме того, чаще всего рассматриваются регулярные методы С., то есть методы, суммирующие каждый сходящийся ряд к его обычной сумме. В большинстве методов С. расходящийся ряд рассматривается в известном смысле как предел сходящегося ряда. А именно, каждый член ряда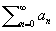 (1)
(1)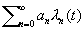 (2)
(2)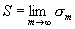 ,
,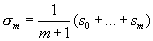 ,
, 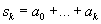 .
.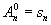 ,
, 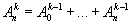 ,
,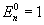 ,
, 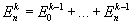 ,
,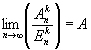 , то говорят, что ряд суммируется к А методом Чезаро k-го порядка. С ростом k возрастает сила метода Чезаро, то есть расширяется множество рядов, суммируемых этим методом. Всякий ряд, суммируемый методом Чезаро какого-либо порядка, суммируется и методом Абеля — Пуассона и притом к той же сумме. Например, ряд 1— 1 + 1 —... + (—1) n-1 +... суммируется методом Абеля — Пуассона к значению 1/2, так как
, то говорят, что ряд суммируется к А методом Чезаро k-го порядка. С ростом k возрастает сила метода Чезаро, то есть расширяется множество рядов, суммируемых этим методом. Всякий ряд, суммируемый методом Чезаро какого-либо порядка, суммируется и методом Абеля — Пуассона и притом к той же сумме. Например, ряд 1— 1 + 1 —... + (—1) n-1 +... суммируется методом Абеля — Пуассона к значению 1/2, так как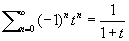 ,
, 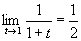 .
.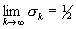 .
.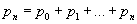 ; обобщённой суммой ряда, по Вороному, называется предел
; обобщённой суммой ряда, по Вороному, называется предел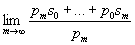 .
.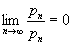 .
.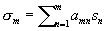 ,
, 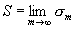 был регулярен. Польский математик Х. Штейнхауз обобщил эти условия на случай квадратных матриц.
был регулярен. Польский математик Х. Штейнхауз обобщил эти условия на случай квадратных матриц.
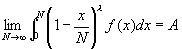 ,
,