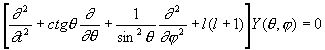 ,
,Сферические функции, специальные функции, применяемые для изучения физических явлений в пространственных областях, ограниченных сферическими поверхностями, и для решения физических задач, обладающих сферической симметрией. С. ф. являются решениями дифференциального уравнения
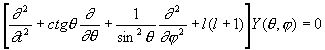 ,
,
получающегося при разделении переменных в Лапласа уравнении в сферических координатах r, q, j. Общий вид решения:
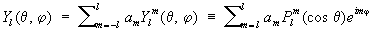 ,
,
где am — постоянные, 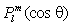 — присоединённые функции Лежандра степени l и порядка m, определяемые равенством:
— присоединённые функции Лежандра степени l и порядка m, определяемые равенством:
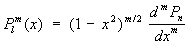 ,
,
где Рп — Лежандра многочлены.
С. ф. можно рассматривать как функции на поверхности единичной сферы. Функции
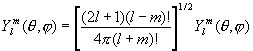
образуют полную ортонормированную систему на сфере, играющую ту же роль в разложении функций на сфере, что тригонометрическая система функций {e imj} на окружности. Функции на сфере, не зависящие от координаты j, разлагаются по зональным С. ф.:
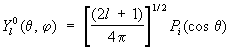
С. ф. степени l
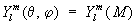
при вращении сферы линейно преобразуется по формуле:
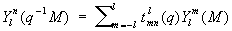 (1)
(1)
(q–1M — точка, в которую переходит точка М сферы при вращении q–1). Коэффициенты 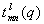 являются матричными элементами неприводимого унитарного представления веса l группы вращения сферы. Их называют также обобщёнными С. ф. Обобщённые С. ф. применяются при разложении векторных и тензорных полей на единичной сфере, решении некоторых задач теории упругости и т. д.
являются матричными элементами неприводимого унитарного представления веса l группы вращения сферы. Их называют также обобщёнными С. ф. Обобщённые С. ф. применяются при разложении векторных и тензорных полей на единичной сфере, решении некоторых задач теории упругости и т. д.
С формулой (1) связана теорема сложения для зональных С. ф.:
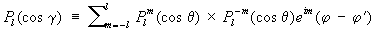 ,
,
где cos g = cos q cos q‘ + sinq sinq' cos (j —j’), g — сферическое расстояние точки (q, j) от точки (q', j’).
Характерным примером многочисленных приложений С. ф. к вопросам математической физики и механики является применение их в теории потенциала. Пусть 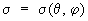 — поверхностная плотность распределения массы по сфере радиуса R с центром в начале координат; если а можно разложить в ряд С. ф.
— поверхностная плотность распределения массы по сфере радиуса R с центром в начале координат; если а можно разложить в ряд С. ф.  , сходящийся равномерно на поверхности сферы, то потенциал, соответствующий этому распределению масс, в каждой точке (r, q, j), внешней относительно данной сферы, равен
, сходящийся равномерно на поверхности сферы, то потенциал, соответствующий этому распределению масс, в каждой точке (r, q, j), внешней относительно данной сферы, равен
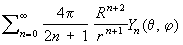
а в каждой точке, внутренней по отношению к сфере, равен
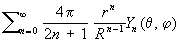
Общий член каждого из этих двух рядов представляет собой шаровую функцию соответственно степени n - 1 и n.
С. ф. были введены А. Лежандром и П. Лапласом в конце 18 в.
Лит.: Бейтмен Г., Эрдей и А., Высшие трансцендентные функции, пер. с англ., т. 1—2, М., 1973; Никифоров А. Ф., Уваров В. Б., Основы теории специальных функций, М., 1974; Гобсон Е. В., Теория сферических и эллипсоидальных функций, пер. с англ., М., 1952; Lense J., Kugelfunktionen, 2 Aufl., Lpz., 1954.