Трансцендентное число число (действительное или мнимое), не удовлетворяющее никакому алгебраическому уравнению с целыми коэффициентами. Таким образом, Т. ч. противопоставляются алгебраическим числам. Существование Т. ч. впервые установил Ж. Лиувилль (1844). Отправной точкой для Лиувилля служила его теорема, согласно которой порядок приближения рациональной дроби с данным знаменателем к данному иррациональному алгебраическому числу не может быть произвольно высоким. Именно, если алгебраическое число а удовлетворяет неприводимому алгебраическому уравнению степени n с целыми коэффициентами, то для любого рационального числа 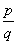 должно выполняться неравенство
должно выполняться неравенство  (с зависит только от a). Поэтому, если для заданного иррационального числа a можно указать бесконечное множество рациональных приближений, не удовлетворяющих приведённому неравенству ни при каких с и n (одних и тех же для всех приближений), то a есть Т. ч. Пример такого числа даёт:
(с зависит только от a). Поэтому, если для заданного иррационального числа a можно указать бесконечное множество рациональных приближений, не удовлетворяющих приведённому неравенству ни при каких с и n (одних и тех же для всех приближений), то a есть Т. ч. Пример такого числа даёт:
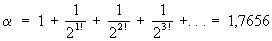 …
…
Другое доказательство существования Т. ч. дал Г. Кантор (1874), заметив, что множество всех алгебраических чисел счётно (то есть все алгебраические числа могут быть перенумерованы; см. Множеств теория), тогда как множество всех действительных чисел несчётно. Отсюда следовало, что множество Т. ч. несчётно, и далее, что Т. ч. составляют основную массу среди множества всех чисел.
Важнейшая задача теории Т. ч. — это выяснение того, являются ли Т. ч. значения аналитических функций, обладающих теми или иными арифметическими и аналитическими свойствами при алгебраических значениях аргумента. Задачи этого рода принадлежат к числу труднейших задач современной математики. В 1873 Ш. Эрмит доказал, что неперово число 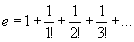 является трансцендентным.
является трансцендентным.
В 1882 немецкий математик Ф. Линдеман получил более общий результат: если a — алгебраическое число, то е a — Т. ч. Результат Липдемана был значительно обобщён немецким математиком К. Зигелем (1930), доказавшим, например, трансцендентность значения широкого класса цилиндрических функций при алгебраических значениях аргумента. В 1900 на математическом конгрессе в Париже Д. Гильберт среди 23 нерешенных проблем математики указал на следующую: является ли трансцендентным числом ab, где a и b — алгебраические числа, причём b — иррациональное число, и, в частности, является ли трансцендентным число 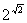 , е p (проблема трансцендентности чисел вида ab была впервые в частной форме поставлена Л. Эйлером, 1744). Полное решение этой проблемы (в утвердительном смысле) удалось получить лишь в 1934 А. О. Гельфонду. Из открытия Гельфонда, в частности, следует, что все десятичные логарифмы натуральных чисел (то есть «табличные логарифмы») суть Т. ч. Методы теории Т. ч. прилагаются к ряду вопросов решения уравнений в целых числах.
, е p (проблема трансцендентности чисел вида ab была впервые в частной форме поставлена Л. Эйлером, 1744). Полное решение этой проблемы (в утвердительном смысле) удалось получить лишь в 1934 А. О. Гельфонду. Из открытия Гельфонда, в частности, следует, что все десятичные логарифмы натуральных чисел (то есть «табличные логарифмы») суть Т. ч. Методы теории Т. ч. прилагаются к ряду вопросов решения уравнений в целых числах.
Лит.: Гельфонд А. О., Трансцендентные и алгебраические числа, М., 1952.
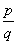 должно выполняться неравенство
должно выполняться неравенство  (с зависит только от a). Поэтому, если для заданного иррационального числа a можно указать бесконечное множество рациональных приближений, не удовлетворяющих приведённому неравенству ни при каких с и n (одних и тех же для всех приближений), то a есть Т. ч. Пример такого числа даёт:
(с зависит только от a). Поэтому, если для заданного иррационального числа a можно указать бесконечное множество рациональных приближений, не удовлетворяющих приведённому неравенству ни при каких с и n (одних и тех же для всех приближений), то a есть Т. ч. Пример такого числа даёт: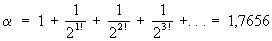 …
…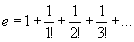 является трансцендентным.
является трансцендентным.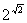 , е
, е