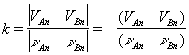 .
.Удар твёрдых тел, совокупность явлений, возникающих при столкновении движущихся твёрдых тел, а также при некоторых видах взаимодействия твёрдого тела с жидкостью или газом (У. струи о тело, У. тела о поверхность жидкости, гидравлический удар, действие взрыва или ударной волны на твёрдое тело и др.). Промежуток времени, в течение которого длится У., обычно очень мал (на практике от нескольких десятитысячных до миллионных долей сек), а развивающиеся на площадках контакта соударяющихся тел силы (называются ударными или мгновенными) очень велики. Изменяются они за время У. в широких пределах и достигают значений, при которых средние величины давления (напряжений) на площадках контакта имеют порядок 104 и даже 105 кгс/см2 (1 кгс/см2 = 102 н/м2). Действие ударных сил приводит к значительному изменению за время У. скоростей точек тела. Следствиями У. могут быть также остаточные деформации, звуковые колебания, нагревание тел, изменение механических свойств их материалов и др., а при скоростях соударения, превышающих критические, — разрушение тел в месте У. Порядок критических скоростей для металлов » 15 м/сек (медь) — 150 м/сек и более (высококачественные стали).
Изменение скоростей точек тела за время У. определяется методами общей теории У., где в качестве меры механического взаимодействия тел при У. вместо самой ударной силы Р вводится её импульс за время У. t (так называемый ударный импульс S). Одновременно, ввиду малости m, импульсами всех неударных сил, таких, например, как сила тяжести, а также перемещениями точек тела за время У. пренебрегают. Основные уравнения общей теории У. вытекают из теорем об изменении количества движения и кинетического момента системы при У. С помощью этих теорем, зная приложенный ударный импульс и скорости в начале У., определяют скорости в конце У., а если тело является несвободным, то и импульсивные реакции связей.
В случае соударения двух тел процесс соударения можно разделить на 2 фазы. 1-я фаза начинается с момента соприкосновения точек А и В тел (см. рис.), имеющих в этот момент скорость сближения νAn — νBn, где νАn и νBn — проекции скоростей νA и νB на общую нормаль n к поверхностям тел в точках А и В, называется линией удара. К концу 1-й фазы сближение тел прекращается, а часть их кинетической энергии переходит в потенциальную энергию деформации. Во 2-й фазе происходит обратный переход потенциальной энергии упругой деформации в кинетическую энергию тел; при этом тела начинают расходиться и к концу 2-й фазы точки А и В будут иметь скорость расхождения VAn — VBn. Для совершенно упругих тел механическая энергия к концу У. восстановилась бы полностью и было бы |VAn—VBn| = |νAn—νBn|, наоборот, У. совершенно неупругих тел закончился бы на 1-й фазе (VAn—VBn= 0). При У. реальных тел механическая энергия к концу У. восстанавливается лишь частично вследствие потерь на сообщение остаточных деформаций, нагревание тел и др. |VAn—VBn|< |νAn—νBn|. Для учёта этих потерь вводится так называемый коэффициент восстановления k, который считается зависящим только от физических свойств материалов тел:
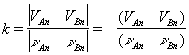 .
.
В случае У. по неподвижному телуVBn=νBn= 0 и k = – VAn /νAn. Значение k определяется экспериментально, например измерением высоты h, на которую отскакивает шарик, свободно падающий на горизонтальную плиту с высоты Н; в этом случае 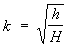 . По данным опытов, при соударении тел из дерева k = 0,5, из стали — 0,55, из слоновой кости — 0,89, из стекла — 0,94. В предельных случаях при совершенно упругом У. k = 1, а при совершенно неупругом k = 0. Зная скорости до У. и коэффициент k, можно найти скорости после У. и действующий в точках соударения ударный импульс S. Ecли центры масс тел C1 и C2 лежат на линии У., то У. называется центральным (У. шаров); в противном случае — нецентральным. Если скорости ν1 и ν2 центров масс в начале У. направлены параллельно линии У., то У. называется прямым; в противном случае — косым. При прямом центральном У, двух гладких тел (шаров) 1 и 2
. По данным опытов, при соударении тел из дерева k = 0,5, из стали — 0,55, из слоновой кости — 0,89, из стекла — 0,94. В предельных случаях при совершенно упругом У. k = 1, а при совершенно неупругом k = 0. Зная скорости до У. и коэффициент k, можно найти скорости после У. и действующий в точках соударения ударный импульс S. Ecли центры масс тел C1 и C2 лежат на линии У., то У. называется центральным (У. шаров); в противном случае — нецентральным. Если скорости ν1 и ν2 центров масс в начале У. направлены параллельно линии У., то У. называется прямым; в противном случае — косым. При прямом центральном У, двух гладких тел (шаров) 1 и 2
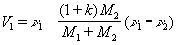 ,
,
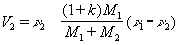 ,
,
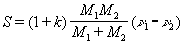 ,
,
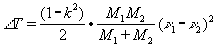 .
.
где DT — потерянная за время У. кинетическая энергия системы, M1 и M2 — массы шаров. В частном случае при k = 1 и M1= M2 получается V1= ν 2 и V2 = ν 1, то есть шары одинаковой массы при совершенно упругом У. обмениваются скоростями; при этом DТ = 0.
Для определения времени У., ударных сил и вызванных ими в телах напряжений и деформаций необходимо учесть механические свойства материалов тел и изменения этих свойств за время У., а также характер начальных и граничных условий. Решение проблемы существенно усложняется не только из-за трудностей чисто математического характера, но и ввиду отсутствия достаточных данных о параметрах, определяющих поведение материалов тел при ударных нагрузках, что заставляет делать при расчётах ряд существенных упрощающих предположений. Наиболее разработана теория У. совершенно упругих тел, в которой предполагается, что тела за время У. подчиняются законам упругого деформирования (см. Упругости теория) и в них не появляется остаточных деформаций. Деформация в месте контакта распространяется в таком теле в виде упругих волн со скоростью, зависящей от физических свойств материала. Если время прохождения этих волн через всё тело много меньше времени У., то влиянием упругих колебаний можно пренебречь и считать характер контактных взаимодействий при У. таким же, как в статическом состоянии. На таких допущениях основывается контактная теория удара Г. Герца. Если же время прохождения упругих волн через тело сравнимо со временем У., то для расчётов пользуются волновой теорией У.
Изучение У. не вполне упругих тел — задача значительно более сложная, требующая учёта как упругих, так и пластических свойств материалов. При решении этой задачи и связанных с ней проблем определения механических свойств материалов тел при У., изучения изменений их структуры и процессов разрушения широко опираются на анализ и обобщение результатов многочисленных экспериментальных исследований. Экспериментально исследуются также специфические особенности У. тел при больших скоростях (порядка сотен м/сек) и при воздействии взрыва, который в случае непосредственного контакта заряда с телом можно считать эквивалентным соударению со скоростью до 1000 м/сек.
Кроме У. твёрдых тел, в физике изучают столкновения молекул, атомов и элементарных частиц (см. также Столкновения атомные).
Лит.: Кильчевский Н. А., Теория соударений твердых тел, Л. — М., 1949; Динник. А. Н., Удар и сжатие упругих тел, Избр. труды, т. 1, К., 1952; Давиденков Н. Н., Динамические испытания металлов, 2 изд., Л.—М., 1936; Ильюшин А. А., Ленский В. С., Сопротивление материалов, М., 1959, гл. 6; Райнхарт Дж., Пирсон Дж., Поведение металлов при импульсивных нагрузках, пер. с англ., М., 1958.
С. М. Тарг.

Схема удара двух тел.