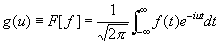 , (1)
, (1)Фурье преобразование (данной функции), функция, выражающаяся через данную функцию f (x) формулой:
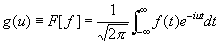 , (1)
, (1)
Если функция f (x) чётная, то её ф. п. равно
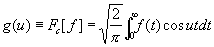 (2)
(2)
(косинус-преобразование), а если f (x) — нечётная функция, то
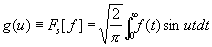 (3)
(3)
(синус-преобразование). Формулы (1), (2) и (3) обратимы, т. е. для чётных функций
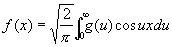 , (4)
, (4)
а для нечётных функций
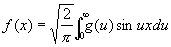 . (5)
. (5)
В общем случае имеет место формула
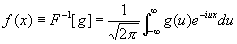 . (6)
. (6)
Каждой операции над функциями соответствует операция над их Ф. п., которая во многих случаях проще соответствующей операции над f (x). Например, Ф. п. f'(x) является iug (u). Если
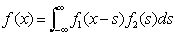 , (7)
, (7)
то g (u) = g1(u) g2(u). Для f (x + а) Ф. п. является eiuag (u), а для c1f1(x) + c2f2 (x) — функция c1g1(u) + c2g2(u).
Если существует 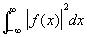 , то интегралы в формулах (1) и (6) сходятся в среднем (см. Сходимость), причём
, то интегралы в формулах (1) и (6) сходятся в среднем (см. Сходимость), причём
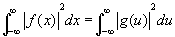 (8)
(8)
(теорема Планшереля). Формула (8) является обобщением на Ф. п. формулы Парсеваля (см. Парсеваля равенство) для рядов Фурье (см. Фурье ряд). Физический смысл формулы (8) заключается в равенстве энергии некоторого колебания сумме энергий его гармонических компонент. Отображение F: f (x) ® g (u) является унитарным оператором в гильбертовом пространстве функций f (x), — ¥ < x < ¥, с интегрируемым квадратом. Этот оператор может быть представлен также в виде
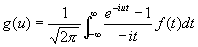 . (9)
. (9)
При некоторых условиях на f (x) справедлива формула Пуассона
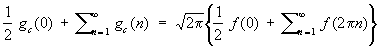 ,
,
находящая применение в теории тэта-функций.
Если функция f (x) достаточно быстро убывает, то её Ф. п. можно определить и при некоторых комплексных значениях u = v + iw. Например, если существует 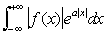 , а > 0, то Ф. п. определено при |w| < а. Ф. п. при комплексных значениях тесно связано с двусторонним преобразованием Лапласа (см. Лапласа преобразование)
, а > 0, то Ф. п. определено при |w| < а. Ф. п. при комплексных значениях тесно связано с двусторонним преобразованием Лапласа (см. Лапласа преобразование)
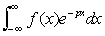
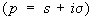 .
.
Оператор Ф. п. может быть расширен на более обширные классы функций, нежели совокупность суммируемых функций [например, для функций f (x) таких, что (1 + |x|)–1f (x) суммируема, Ф. п. определяется формулой (9)], и даже на некоторые классы обобщённых функций (т. н. медленного роста).
Имеются обобщения Ф. п. Одно из них использует различного рода специальные функции, например Бесселя функции, это направление получает завершение в теории представлений непрерывных групп. Другим является т. н. преобразование Фурье — Стилтьеса, широко применяемое, например, в теории вероятностей; оно определяется для произвольной ограниченной неубывающей функции j(x) Стилтьеса интегралом
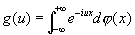 (10)
(10)
и называется характеристической функцией распределения j. Для представимости функции g (u) в виде (10) необходимо и достаточно, чтобы при любых u1,..., un, x1,...,xn было
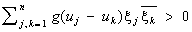
(теорема Бохнера — Хинчина).
Ф. п., первоначально возникшее в теории теплопроводности, имеет многочисленные применения как в самой математике (например, при решении дифференциальных, разностных и интегральных уравнений, в теории специальных функций и т.д.), так и в различных разделах теоретической физики. Например, Ф. п. стало стандартным аппаратом квантовой теории поля, широко используется в методе функций Грина для неравновесных задач квантовой механики и термодинамики, в теории рассеяния и т.д.
Лит.: Снеддон И., Преобразование Фурье, пер. с англ., М., 1955; Владимиров В. С., Обобщенные функции в математической физике, М., 1976.