 + (Iz — Iy) wywz = Mx,
+ (Iz — Iy) wywz = Mx,Эйлера уравнения,
1) в механике — динамические и кинематические уравнения, используемые при изучении движения твёрдого тела; даны Л. Эйлером в 1765.
Динамические Э. у. представляют собой дифференциальные уравнения движения твёрдого тела вокруг неподвижной точки и имеют вид
Ix + (Iz — Iy) wywz = Mx,
+ (Iz — Iy) wywz = Mx,
Iy + (Ix — Iz) wzwx = My, (1)
+ (Ix — Iz) wzwx = My, (1)
Iz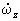 + (Iy — Ix) wxwy = Mz,
+ (Iy — Ix) wxwy = Mz,
где Ix, Iy, Iz — моменты инерции тела относительно гл. осей инерции, проведённых из неподвижной точки, wх, wу, wz — проекции мгновенной угловой скорости тела на эти оси, Mx, My, Mz — гл. моменты сил, действующих на тело, относительно тех же осей; 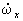 ,
, 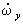 ,
, 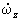 — проекции углового ускорения.
— проекции углового ускорения.
Кинематические Э. у. дают выражения wх, wу, wz через Эйлеровы углы j, y, q и имеют вид
wx= 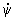 sin q sinj +
sin q sinj + 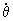 cosj,
cosj,
wу= 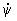 sin q cosj —
sin q cosj — 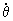 sinj, (2)
sinj, (2)
wz= 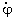 +
+ 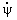 cos q.
cos q.
Система уравнений (1) и (2) позволяет, зная закон движения тела, определить момент действующих на него сил, и, наоборот, зная действующие на тело силы, определить закон его движения.
2) В гидромеханике — дифференциальные уравнения движения идеальной жидкости в переменных Эйлера. Если давление р, плотность r, проекции скоростей частиц жидкости u, u, w и проекции действующей объёмной силы X, У, Z рассматривать как функции координат x, у, z точек пространства и времени t (переменные Эйлера), то Э. у. в проекциях на прямоугольные декартовы оси координат будут:
 ,
,
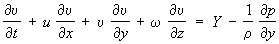 ,
,
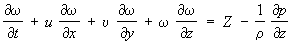 .
.
Решение общей задачи гидромеханики в переменных Эйлера сводится к тому, чтобы, зная X, У, Z, а также начальные и граничные условия, определить u, u, w, р, r, как функции х, у, z и t. Для этого к Э. у. присоединяют уравнение неразрывности в переменных Эйлера
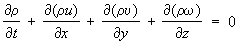 .
.
В случае баротропной жидкости, у которой плотность зависит только от давления, 5-м уравнением будет уравнение состояния r = j (р) (или r — const, когда жидкость несжимаема).
Э. у. пользуются при решении разнообразных задач гидромеханики.
Лит.: Бухгольц Н. Н., Основной курс теоретической механики, ч. 2, 9 изд., М., 1972, §14, 16; Лойцянский Л. Г., Механика жидкости и газа, 4 изд., М., 1973.
С. М. Тарг.