Эффективное поперечное сечение, эффективное сечение, сечение (в физике), величина, характеризующая вероятность перехода системы двух сталкивающихся частиц в результате их рассеяния (упругого или неупругого) в определённое конечное состояние. Э. п. с. s равно отношению числа dN таких переходов в единицу времени к плотности nv потока рассеиваемых частиц, падающих на мишень, т. е. к числу частиц, проходящих в единицу времени через единичную площадку, перпендикулярную к их скорости v (n — плотность числа падающих частиц): s = dN/nv. Таким образом, Э. п. с. имеет размерность площади; обычно оно измеряется в см2. Различным типам переходов, наблюдаемых при рассеянии частиц, соответствуют разные Э. п. с. Упругое рассеяние частиц характеризуют дифференциальным Э. п. с. d s/d W, равным отношению числа частиц, упруго рассеянных в единицу времени в единицу телесного угла, к потоку падающих частиц (d W — элемент телесного угла), и полным сечением s, равным интегралу дифференциального сечения, взятому по полному телесному углу (W = 4p стер). Для иллюстрации на рис. схематически изображен процесс упругого рассеяния точечных «классических» частиц на шарике радиуса R0 с «абсолютно жёсткой» поверхностью. Полное Э. п. С. рассеяния для этого случая равно геометрическому сечению шарика: s = pR02.
При наличии неупругих процессов полное сечение складывается из Э. п. с. упругих и неупругих процессов. Для более детальной характеристики рассеяния вводят сечение для отдельных типов (каналов) неупругих реакций. Для множественных процессов важное значение имеют т. н. инклюзивные сечения, описывающие вероятность появления в данном столкновении какой-либо определённой частицы или группы частиц.
Если взаимодействие между сталкивающимися частицами велико и быстро падает с расстоянием, то Э. п. с. по порядку величины, как правило, равно квадрату радиуса действия сил или геометрическому сечению системы (см. рис.); однако вследствие специфических квантовомеханических явлений Э. п. с. могут существенно отличаться от этих значений (например, в случаях резонансного рассеяния и Рамзауэра эффекта).
Экспериментальные измерения Э. п. с. рассеяния дают сведения о структуре сталкивающихся частиц. Так, измерения сечения упругого рассеяния a-частиц атомами позволили открыть атомное ядро, а упругого рассеяния электронов протонами и нейтронами (нуклонами) — определить радиусы нуклонов и распределение в них электрического заряда и магнитного момента (т. н. формфакторы). Понятие Э. п. с. используется также в статистической физике при построении кинетических уравнений.
С. С. Герштейн.

Схема, поясняющая упругое рассеяние «классической» частицы на «абсолютно твёрдом» шарике. Рассеянию на угол J = p - a отвечает параметр столкновения r = R0sin(a/2) = R0cos(J/2), а сечение ds рассеяния в телесный угол dW = 2psinJdJ равно площади заштрихованного кольца: dJ = 2prdr = (p/2)R sinJdJ, т. е. дифференциальное сечение ds/dW = R
sinJdJ, т. е. дифференциальное сечение ds/dW = R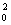 /4, а полное сечение упругого рассеяния равно геометрическому сечению шарика: s = pR
/4, а полное сечение упругого рассеяния равно геометрическому сечению шарика: s = pR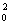 . При учёте квантовых (волновых) свойств частиц сечение получается иным. В предельном случае l >> R0 (l = ħ/r — длина волны де Бройля частицы, r — её импульс, ħ — постоянная Планка) рассеяние сферически симметрично, а полное сечение в 4 раза больше классического: sкв = 4pR02. При l << R0 рассеяние на конечные углы (J ¹ 0) напоминает классическое, однако под очень малыми углами dJ~l/R0 происходит волновое «дифракционное» рассеяние с сечением pR
. При учёте квантовых (волновых) свойств частиц сечение получается иным. В предельном случае l >> R0 (l = ħ/r — длина волны де Бройля частицы, r — её импульс, ħ — постоянная Планка) рассеяние сферически симметрично, а полное сечение в 4 раза больше классического: sкв = 4pR02. При l << R0 рассеяние на конечные углы (J ¹ 0) напоминает классическое, однако под очень малыми углами dJ~l/R0 происходит волновое «дифракционное» рассеяние с сечением pR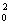 ; т. о., полное сечение с учётом дифракции вдвое больше классического: s = 2pR
; т. о., полное сечение с учётом дифракции вдвое больше классического: s = 2pR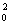 .
.
 sinJdJ, т. е. дифференциальное сечение ds/dW = R
sinJdJ, т. е. дифференциальное сечение ds/dW = R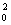 /4, а полное сечение упругого рассеяния равно геометрическому сечению шарика: s = pR
/4, а полное сечение упругого рассеяния равно геометрическому сечению шарика: s = pR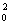 . При учёте квантовых (волновых) свойств частиц сечение получается иным. В предельном случае l >> R0 (l = ħ/r — длина волны де Бройля частицы, r — её импульс, ħ — постоянная Планка) рассеяние сферически симметрично, а полное сечение в 4 раза больше классического: sкв = 4pR02. При l << R0 рассеяние на конечные углы (J ¹ 0) напоминает классическое, однако под очень малыми углами dJ~l/R0 происходит волновое «дифракционное» рассеяние с сечением pR
. При учёте квантовых (волновых) свойств частиц сечение получается иным. В предельном случае l >> R0 (l = ħ/r — длина волны де Бройля частицы, r — её импульс, ħ — постоянная Планка) рассеяние сферически симметрично, а полное сечение в 4 раза больше классического: sкв = 4pR02. При l << R0 рассеяние на конечные углы (J ¹ 0) напоминает классическое, однако под очень малыми углами dJ~l/R0 происходит волновое «дифракционное» рассеяние с сечением pR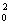 ; т. о., полное сечение с учётом дифракции вдвое больше классического: s = 2pR
; т. о., полное сечение с учётом дифракции вдвое больше классического: s = 2pR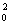 .
.