Винтовые линии, движения и поверхности
Винтовые линии, движения и поверхности
Винтовые линии, цилиндрические и конические, суть кривые двоякой кривизны, начерченные первые на прямой круглой цилиндрической, а последние — на прямой круговой конической поверхности и пересекающие прямолинейные производящие под постоянным для каждой кривой углом. В. линия на цилиндре радиуса R, пересекающая прямолинейные производящие цилиндра под углом (π/2 — α), имеет везде одинаковые радиусы кривизны (см. Радиус кривизны) и второй кривизны; эти радиусы равны:
- R/cos²α , R/(sin α • cos α).
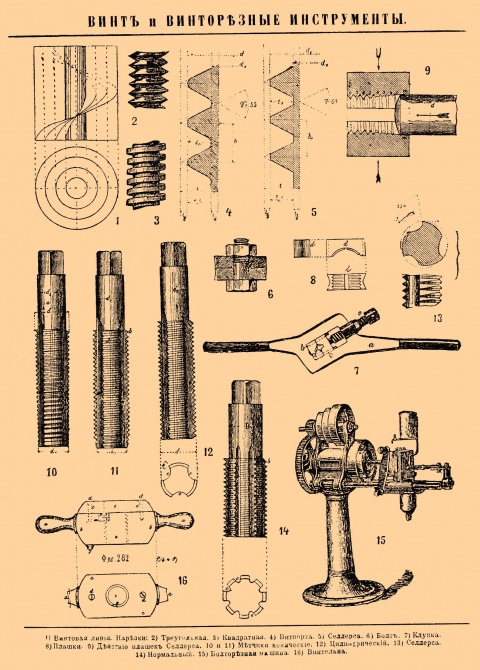
Кроме цилиндрических винтовых линий, никакие другие линии двоякой кривизны не обладают постоянными радиусами первой и второй кривизны на всем своем протяжении. Главная нормаль в каждой точке В. линии пересекает ось цилиндра и перпендикулярна к ней. Геометрическое место пересечения касательных к В. цилиндрической линии с плоскостью основания цилиндра есть развертка, или эвольвента, круга основания. Винтовым шагом, или высотою витка, называется расстояние h между ближайшими между собою точками пересечения винтовой линии одною и тою же производящею цилиндра. Отношение величины шага h к окружности 2•π•R основания есть подъем винта. Ось цилиндра есть винтовая ось. Если развернуть цилиндрическую поверхность на плоскость, то цилиндрическая В. линия обратится в прямую линию. Проекция цилиндрической В. л. на плоскость, параллельную винтовой оси, есть синусоида. На фиг. 1-й таблицы «Винт и Винторезные инструменты» изображены проекции четырех винтовых линий одного шага и разных подъемов.
Винтовая линия на прямом круговом конусе пересекает все прямолинейные производящие конич. поверхности под одним и тем же углом, но радиусы первой и второй кривизны в разных точках ее пропорциональны расстоянию точек от вершины; отношение же обоих радиусов имеет постоянную величину, зависящую от наклона кривой к основанию конуса. Проекция конической В. линии на плоскость основания есть логарифмическая спираль. Если развернуть конич. поверхн. на плоскость, то коническая В. л. обратится в логарифмическую спираль. Две винтовые линии, начерченные на одной и той же поверхности и пересекающие производящие под одинаковыми углами, не могут быть совмещены одна с другою, если одна из них есть правовинтовая, а другая — левовинтовая.

Винтовые движения. Точка совершает винтовое движение, если траектория ее есть право- или левовинтовая цилиндрическая кривая (см. Винтовые линии). При этом скорость точки может быть постоянною (тогда винтовое движение равномерное) или переменною. Винтовое движение твердого тела есть такое, при котором все точки его описывают винтовые линии вокруг одной и той же оси с одинаковым винтовым шагом. Оно может быть разложено на поступательное движение параллельно оси и на вращательное движение вокруг этой оси. Если вращение совершается вправо по отношению к наблюдателю, плывущему по направлению поступательного движения, то винтовое движение тела есть левовинтовое; в противном случае оно правовинтовое. Поступательное движение и вращение вокруг постоянной оси можно рассматривать как крайние случаи винтовых движений. При первом винтовой шаг бесконечно велик, при втором — равен нулю. Означим чрез W скорость поступательного движения твердого тела параллельно винтовой оси, через ω — угловую скорость вращения, через h величину шага винтовых траекторий точек тела; между этими тремя величинами существует следующая зависимость: W/ ω = h/2 π. Если отношение скорости поступательной к угловой скорости изменяется, то твердое тело совершает винтовое движение с изменяющимся шагом. Самые сложные движения твердого тела можно рассматривать как винтовые движения с изменяющимся шагом вокруг изменяющей свое положение винтовой оси.
Винтовые поверхности, или геликоиды, образуются в пространстве движением прямой или кривой линии, неизменно связанной с твердым телом, совершающим винтовое движение с постоянным шагом вокруг какой-либо постоянной оси; эта ось есть вместе с тем и ось геликоида. Линейчатые винтовые поверхности получаются тогда, когда производящая есть прямая. Смотря по величине кратчайшего расстояния производящей от винтовой оси, по величине угла между ними и по величине шага винта, линейчатые геликоиды могут быть весьма разнообразны. Если производящая пересекает винтовую ось, то образуется линейчатый геликоид с прямолинейною направляющею; а если производящая перпендикулярна к пересекаемой ею винтовой оси, то получается обыкновенная винтовая поверхность, называемая также В. поверхностью с направляющею плоскостью (перпендикулярною к винтовой оси). Находящаяся в табл. Гребные винты фиг. 1 дает понятие о виде этой В. поверхности.
Когда производящая не пересекает винтовую ось и винтовой шаг равен нулю, то В. поверхность обращается в гиперболоид вращения. Самое узкое сечение этой линейчатой поверхности, шейка ее, есть круг, описываемый тою точкою производящей, которая находится в кратчайшем расстоянии от оси вращения. Этот круг есть вместе с тем стрикционная линия гиперболоида. Каждая не развертываемая на плоскость (иначе говоря, косая) линейчатая поверхность имеет некоторую стрикционную линию; под этим именем подразумевается кривая, проходящая через середины кратчайших расстояний между соседними производящими. Если производящая линейчатого геликоида не пересекает винтовую ось, то вся поверхность находится вне той цилиндрической поверхности, на которой ближайшая к винтовой оси точка производящей вычерчивает так называемую основную винтовую кривую. Если производящая не касательна к этой кривой, то геликоид косой и основная винтовая линия есть стрикционная линия его. Если же производящая касательна к основной винтовой кривой, то получается геликоид, развертываемый на плоскость. Основная винтовая линия служит кривою возврата (см. Возвратные точки и кривые) этой поверхности. Всякое сечение этой поверхности плоскостью, перпендикулярною к винтовой оси, есть развертка, или эвольвента, круга основания внутренней цилиндрической поверхности. При развертывании этого геликоида на плоскость прямолинейные производящие обращаются в прямые, касательные к той окружности, в которую обращается кривая возврата, а сечение геликоида плоскостью перпендикулярною к винтовой оси обращается в развертку этой окружности. Модель такого геликоида можно сделать из бумаги. Из винтовых поверхностей нелинейчатых замечательны: та, на поверхность которой налагается поверхность сферического пояса, и другие, на поверхности которых налагаются пояса соответственных планетарных эллипсоидов. Об этих поверхностях см. статью Бура (Bour) «Théorie de la dé formation des surfaces» в «Journal de l' école polytechnique», Cahier 39.
- В статье воспроизведен материал из Большого энциклопедического словаря Брокгауза и Ефрона.
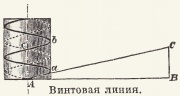
Винтовая линия, кривая линия (на рис. Aacb), начерченная на поверхности круглого цилиндра, которая, по развертывании поверхности цилиндра в плоскость, преобразуется в прямую линию (АС, см. рис. на ст. 160).
- В статье воспроизведен текст из Малой советской энциклопедии.