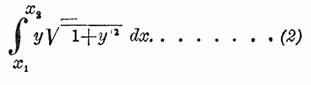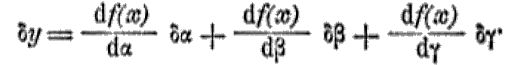Вариационное исчисление — различия между версиями
EvgBot (обсуждение | вклад) м (Новая страница: «'''Вариационное исчисление''', отдел математического анализа, занимающийся разысканием так…») |
EvgBot (обсуждение | вклад) м |
||
| Строка 1: | Строка 1: | ||
| + | '''Вариационное исчисление''' | ||
| + | |||
| + | — История происхождения вариационного исчисления следующая: в конце [[XVII]] и начале [[XVIII]] столетия многие знаменитые геометры, как, например, [[Ньютон]], Иоанн и Яков [[Бернулли]], [[Лейбниц]], [[Маклорен]] и др., обратили внимание на особый род математических вопросов, в которых требовалось определить вид кривой линии или поверхности при условии, чтобы некоторая величина, зависящая от вида кривой или поверхности, была наибольшая или наименьшая. Впервые встречается подобный вопрос в книге Ньютона: «Philosophiae naturalis principia mathematica», а именно вопрос о форме поверхности тела вращения, испытывающего наименьшее сопротивление движению со стороны окружающей его среды. Другой вопрос того же рода — вопрос о виде ''брахистохроны'', предложенный Иоанном Бернулли ([[брахистохрона|брахистохроной]] для какой-либо силы называют кривую, по которой [[материальная точка]], подверженная этой силе, переходит в наивозможно краткое время из одной данной точки в другую). По мере накопления подобных вопросов выяснилась необходимость изыскать общий метод для их решения. Такой метод создан [[Эйлер]]ом («Меthodus inveniendi lineas curvas maximi vel minimi proprietate gaudentes…» [[1744]]) после 16-летних изысканий над решениями разнообразных вопросов этого рода, и усовершенствован [[Лагранж]]ем (см. «Théorie des Fonctions analytiques» и «Leçons sur le Calcul des Fonctions»). Метод этот есть метод вариаций и назван Лагранжем вариационным исчислением (''Calcul des variations''). | ||
| + | |||
| + | Простейшие вопросы вариационного исчисления заключаются в следующем: требуется найти такую функцию от ''x'', которая, будучи подставлена вместо ''у'' в данную функцию ''F'' от ''х'', '' у'',''dy''/''dx'',''d''<sup>2</sup>''y''/''dx''<sup>2</sup>..., дала бы интегралу | ||
| + | |||
| + | [[Файл:Вариационное исчисление b10 523-1.jpg|center]] | ||
| + | |||
| + | наибольшую или наименьшую величину, при предположении, что ''х'' <sub>1</sub> и ''x''<sub>2</sub>, а также и соответствующие им ''у''<sub>1</sub> и ''у''<sub>2</sub> имеют данные постоянные значения. Например, требуется найти кратчайшую кривую на плоскости между двумя данными точками. В этом случае [[интеграл]], который должен получить [[наименьшее значение]], будет | ||
| + | |||
| + | [[Файл:Вариационное исчисление b10 523-2.jpg|center]] | ||
| + | |||
| + | где ''x''<sub>1</sub> и ''x''<sub>2</sub> суть абциссы данных точек. | ||
| + | |||
| + | |||
| + | |||
| + | Другой пример: требуется провести такую кривую ''y'' = ''f''(''x'') между двумя точками (''х''<sub>1</sub>, ''у''<sub>1</sub>) и (''x''<sub>2</sub>, ''y''<sub>2</sub>) на плоскости, чтобы поверхность, образуемая этою кривою при вращении плоскости вокруг оси ''X'' -ов, была наименьшею. В этом случае интеграл, долженствующий получить наименьшее значение, будет: | ||
| + | |||
| + | [[Файл:Вариационное исчисление b10 523-3.jpg|center]] | ||
| + | |||
| + | Метод решения подобных вопросов мы вкратце здесь изложим, главным образом для того, чтобы объяснить смысл слов: ''вариация'' и ''вариирование''. Предположим, что искомая функция ''f''(''x'') найдена и что проведена кривая линия ''y'' = ''f''(''x''), делающая интеграл ''S'' наибольшим или наименьшим. В функции ''f''(''x''), кроме ''x'' заключается один или несколько ''параметров'', в качестве коэффициентов, оснований степеней, показателей и проч. Изменяя непрерывным образом величины этих параметров, мы получим другие кривые, отличающиеся видом и положением от искомой нами. При изменении параметров на бесконечно малые величины получим кривые, бесконечно близкие к рассматриваемой. Под ''вариацией'' от ''у'' подразумевается разность между ординатою бесконечно близкой кривой и ординатою рассматриваемой кривой при той же [[абцисса|абциссе]]. Следовательно, вариация [[ордината|ординаты]] ''у'' есть приращение (положительное или отрицательное), получаемое этою ординатою при переходе от рассматриваемой кривой к кривой бесконечно близкой; это приращение обозначается через δ''у''. Выше было сказано, что бесконечно близкая кривая получается через бесконсчно малое изменение параметров. Пусть параметры ''f''(''x'') суть α, β, γ; бесконечно малые приращения их означим через δα, δβ, δγ. Пренебрегая бесконечно малыми величинами второго и высших порядков, можем выразить δ''у'' так: | ||
| + | |||
| + | [[Файл:Вариационное исчисление b10 523-4.jpg|center]] | ||
| + | |||
| + | {{Черновик}} | ||
| + | {{БЭСБЕ}} | ||
| + | |||
'''Вариационное исчисление''', отдел математического анализа, занимающийся разысканием такого рода функций, которые обращают какое-нибудь заданное выражение в максимум или минимум. Напр. найти линию — кратчайшее расстояние между двумя точками (прямая линия). Вариационное исчисление имеет большое применение в [[математика|математике]], [[механика|механике]] и [[теоретическая физика|теоретической физике]]. | '''Вариационное исчисление''', отдел математического анализа, занимающийся разысканием такого рода функций, которые обращают какое-нибудь заданное выражение в максимум или минимум. Напр. найти линию — кратчайшее расстояние между двумя точками (прямая линия). Вариационное исчисление имеет большое применение в [[математика|математике]], [[механика|механике]] и [[теоретическая физика|теоретической физике]]. | ||
Версия 04:10, 11 мая 2012
Вариационное исчисление
— История происхождения вариационного исчисления следующая: в конце XVII и начале XVIII столетия многие знаменитые геометры, как, например, Ньютон, Иоанн и Яков Бернулли, Лейбниц, Маклорен и др., обратили внимание на особый род математических вопросов, в которых требовалось определить вид кривой линии или поверхности при условии, чтобы некоторая величина, зависящая от вида кривой или поверхности, была наибольшая или наименьшая. Впервые встречается подобный вопрос в книге Ньютона: «Philosophiae naturalis principia mathematica», а именно вопрос о форме поверхности тела вращения, испытывающего наименьшее сопротивление движению со стороны окружающей его среды. Другой вопрос того же рода — вопрос о виде брахистохроны, предложенный Иоанном Бернулли (брахистохроной для какой-либо силы называют кривую, по которой материальная точка, подверженная этой силе, переходит в наивозможно краткое время из одной данной точки в другую). По мере накопления подобных вопросов выяснилась необходимость изыскать общий метод для их решения. Такой метод создан Эйлером («Меthodus inveniendi lineas curvas maximi vel minimi proprietate gaudentes…» 1744) после 16-летних изысканий над решениями разнообразных вопросов этого рода, и усовершенствован Лагранжем (см. «Théorie des Fonctions analytiques» и «Leçons sur le Calcul des Fonctions»). Метод этот есть метод вариаций и назван Лагранжем вариационным исчислением (Calcul des variations).
Простейшие вопросы вариационного исчисления заключаются в следующем: требуется найти такую функцию от x, которая, будучи подставлена вместо у в данную функцию F от х, у,dy/dx,d2y/dx2..., дала бы интегралу
наибольшую или наименьшую величину, при предположении, что х 1 и x2, а также и соответствующие им у1 и у2 имеют данные постоянные значения. Например, требуется найти кратчайшую кривую на плоскости между двумя данными точками. В этом случае интеграл, который должен получить наименьшее значение, будет
где x1 и x2 суть абциссы данных точек.
Другой пример: требуется провести такую кривую y = f(x) между двумя точками (х1, у1) и (x2, y2) на плоскости, чтобы поверхность, образуемая этою кривою при вращении плоскости вокруг оси X -ов, была наименьшею. В этом случае интеграл, долженствующий получить наименьшее значение, будет:
Метод решения подобных вопросов мы вкратце здесь изложим, главным образом для того, чтобы объяснить смысл слов: вариация и вариирование. Предположим, что искомая функция f(x) найдена и что проведена кривая линия y = f(x), делающая интеграл S наибольшим или наименьшим. В функции f(x), кроме x заключается один или несколько параметров, в качестве коэффициентов, оснований степеней, показателей и проч. Изменяя непрерывным образом величины этих параметров, мы получим другие кривые, отличающиеся видом и положением от искомой нами. При изменении параметров на бесконечно малые величины получим кривые, бесконечно близкие к рассматриваемой. Под вариацией от у подразумевается разность между ординатою бесконечно близкой кривой и ординатою рассматриваемой кривой при той же абциссе. Следовательно, вариация ординаты у есть приращение (положительное или отрицательное), получаемое этою ординатою при переходе от рассматриваемой кривой к кривой бесконечно близкой; это приращение обозначается через δу. Выше было сказано, что бесконечно близкая кривая получается через бесконсчно малое изменение параметров. Пусть параметры f(x) суть α, β, γ; бесконечно малые приращения их означим через δα, δβ, δγ. Пренебрегая бесконечно малыми величинами второго и высших порядков, можем выразить δу так:
- В статье воспроизведен материал из Большого энциклопедического словаря Брокгауза и Ефрона.
Вариационное исчисление, отдел математического анализа, занимающийся разысканием такого рода функций, которые обращают какое-нибудь заданное выражение в максимум или минимум. Напр. найти линию — кратчайшее расстояние между двумя точками (прямая линия). Вариационное исчисление имеет большое применение в математике, механике и теоретической физике.
- В статье воспроизведен текст из Малой советской энциклопедии.