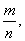
Дробь в арифметике, число, составленное из целого числа долей единицы. Д. изображается символом
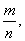
где m — числитель Д. — показывает число взятых долей единицы, разделённой на столько долей, сколько показывает (знаменует) знаменатель n. Д. можно рассматривать как частное от деления одного целого числа (m) на другое (n). Если m делится нацело на n, то частное
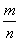
обозначает целое число, например,
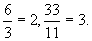
В случае, когда это не так, частное
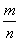
является дробным числом, например,
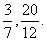
Числитель и знаменатель Д. можно одновременно умножать или делить на одно и то же число, не изменяя величины Д. Всякую Д. можно представить посредством сокращения в виде несократимой, т. е. такой, у которой числитель и знаменатель не имеют общих множителей, например 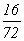 есть сократимая Д.
есть сократимая Д.
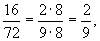
а 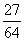 несократимая. Чтобы сложить Д. с общим знаменателем, надо сложить их числители и оставить тот же знаменатель:
несократимая. Чтобы сложить Д. с общим знаменателем, надо сложить их числители и оставить тот же знаменатель:
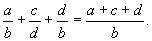
Чтобы сложить несколько Д. с разными знаменателями, надо предварительно привести их к общему знаменателю. Подобным же образом совершается вычитание Д. Чтобы перемножить несколько Д., надо произведение числителей разделить на произведение знаменателей:
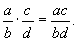
Определяя деление как действие, обратное умножению, получают следующее правило деления Д.:
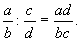
Если числитель Д. меньше знаменателя, то Д. называется правильной, в противном случае — неправильной. Неправильная Д. может быть представлена в виде суммы целого числа и правильной Д. (смешанного числа). Для этого надо числитель разделить (с остатком) на знаменатель. Например,
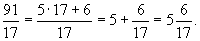
Это положение элементарной арифметики обобщается на любые действительные числа: действительное число х можно единственным образом представить в виде х = n + d, где n — целое и 0 £ d < 1. Число n называется целой частью х и обозначается [x]. Число d = х — [x] называется дробной частью х.
Десятичной дробью называется Д., знаменатель которой есть степень 10. Такую Д. пишут без знаменателя; например,
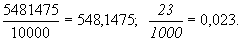
О непрерывных Д. см. Непрерывная дробь.
Операции над Д. встречаются уже в древнеегипетском папирусе Ахмеса (около 2000 до н. э.), где считаются допустимыми только Д. Вида
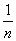
(аликвотные Д.), а потому ставится своеобразная «египетская» задача о представлении любой Д. суммой неравных между собой Д. вида
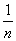
(к последним, в виде исключения, присоединялась ещё Д. 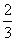 ). Например,
). Например,
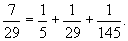
В древневавилонских памятниках письменности встречаются так называемые сексагезимальные Д., т. е. Д., знаменатель которых есть степень 60, игравшие большую роль в античной арифметике; деление единицы на 60 и 3600 = 602 частей сохранилось и до настоящего времени в делении часа или градуса на 60 мин

и каждой минуты на 60 сек. У древних индийцев, по-видимому, впервые зародилось современное обозначение Д.
Лит.: Энциклопедия элементарной математики, кн. 1 — Арифметика, М.—Л., 1951; Депман И. Я., История арифметики, 2 изд., М., 1965.