Логика (греч. logik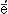 ), наука о приемлемых способах рассуждения. Слово «Л.» в его современном употреблении многозначно, хотя и не столь богато смысловыми оттенками, как древнегреч. lógos, от которого оно происходит. В духе традиции с понятием Л. связываются три основных аспекта: онтологический — «Л. вещей», т. е. необходимая связь явлений объективного мира (Демокрит); гносеологический — «Л. знания», т. е. необходимая связь понятий, посредством которой познаётся «сущность и истина» (Платон), и демонстративный (доказательный), или собственно логический, — «Л. доказательств и опровержений», т. е. необходимая связь суждений (высказываний) в рассуждениях (умозаключениях), принудительная убедительность («общезначимость») которых вытекает только из формы этой связи безотносительно к тому, выражают эти суждения «сущность и истину» или нет (Аристотель). Первые два аспекта относятся к философии и диалектической логике, последний же аспект составляет собственно логику, или современную Л. (которую вслед за И. Кантом иногда называют формальной Л.).
), наука о приемлемых способах рассуждения. Слово «Л.» в его современном употреблении многозначно, хотя и не столь богато смысловыми оттенками, как древнегреч. lógos, от которого оно происходит. В духе традиции с понятием Л. связываются три основных аспекта: онтологический — «Л. вещей», т. е. необходимая связь явлений объективного мира (Демокрит); гносеологический — «Л. знания», т. е. необходимая связь понятий, посредством которой познаётся «сущность и истина» (Платон), и демонстративный (доказательный), или собственно логический, — «Л. доказательств и опровержений», т. е. необходимая связь суждений (высказываний) в рассуждениях (умозаключениях), принудительная убедительность («общезначимость») которых вытекает только из формы этой связи безотносительно к тому, выражают эти суждения «сущность и истину» или нет (Аристотель). Первые два аспекта относятся к философии и диалектической логике, последний же аспект составляет собственно логику, или современную Л. (которую вслед за И. Кантом иногда называют формальной Л.).
Исторически предмет (собственно) Л. ограничивался своего рода «каталогизацией» правильных аргументов, т. е. таких способов рассуждений, которые позволяли бы из истинных суждений-посылок всегда получать истинные суждения-заключения. Известным со времён античности набором таких аргументов однозначно определялся процесс дедукции, характерный для т. н. традиционной Л., ядро которой составляла силлогистика, созданная Аристотелем. По мере изучения особенностей демонстративного мышления предмет традиционной Л. постепенно расширялся за счёт несиллогистических, хотя и дедуктивных способов рассуждений, а также за счёт индукции. Поскольку последняя выпадала из рамок Л. как дедуктивной теории (или совокупности таких теорий), она в конце концов сделалась предметом особой теории, названной индуктивной Л.
Современная Л. является историческим преемником традиционной Л. и в некотором смысле её прямым продолжением. Но в отличие от традиционной, для современной Л. характерно построение различного рода формализованных теорий логического рассуждения — т. н. логических «формализмов», или логических исчислений, позволяющих сделать логические рассуждения предметом строгого анализа и тем самым полнее описать их свойства (см. раздел Предмет и метод современной логики). Отображение логического мышления в логических исчислениях привело к более адекватному выражению идеи «логоса» как единства языка и мышления, чем это было в эпоху античности и во все эпохи, предшествовавшие 20 в.; в современной Л. это выражение столь очевидно, что, исходя из различных «формализмов», приходится порой говорить о различных «стилях логического мышления».
М. М. Новосёлов.
История логики. Историческую основу современной Л. образуют две теории дедукции, созданные в 4 в. до н. э. древнегреческими мыслителями: одна — Аристотелем, другая — его современниками и философскими противниками, диалектиками мегарской школы. Преследуя одну цель — найти «общезначимые» законы логоса, о которых говорил Платон, они, столкнувшись, как бы поменяли исходные пути к этой цели. Известно, что основатель мегарской философской школы Евклид из Мегары широко использовал не только доказательства от противного, но и аргументы, по форме близкие к силлогическим, и таковы многие дошедшие до нас софизмы мегариков. В свою очередь, Аристотель в сочинении «Топика» в качестве доказывающего сформулировал основное правило исчисления высказываний — правило «отделения заключения» (разрешающее при истинности высказываний «если А, то В» и «А» как истинное заключение «отделить» высказывание «В»). И если затем он оставил в стороне Л. высказываний, то в этом «повинны» в немалой степени софизмы мегариков, которые привели Аристотеля к поискам логических элементов речи в элементарной сё единице — предложении. Именно на этом пути он ввёл понятие высказывания как истинной или ложной речи, открыл, в отличие от грамматической, атрибутивную форму речи — как утверждения или отрицания «чего-либо о чём-то», определил «простое» высказывание как атрибутивное отношение двух терминов, открыл изоморфизм атрибутивных и объёмных отношений, аксиому и правила силлогизма. Аристотель создал весьма ограниченную по своим возможностям, но зато законченную теорию — силлогистику, реализующую в рамках Л. классов идею алгорифмизации вывода заключений. Аристотелевская силлогистика положила конец «силлогистике» мегариков, последним представителем которой был Евбулид из Милета, писавший против Аристотеля, автор известных парадоксов «лжец», «лысый», «куча» и нескольких софизмов. Др. последователи Евклида обратились к анализу условных высказываний, считая, что заключения «о присущем», выражаемые фигурами силлогизма, нуждаются в более общей основе. Диодор Крон из Иаса и его ученик Филон из Мегары ввели понятие импликации и изучали связь импликации и отношения следования, предвосхитив идею теоремы о дедукции. Соглашаясь в том, что условное высказывание — импликация — истинно, когда заключение следует из посылки, они расходились, однако, в толковании понятия «следует». Согласно Диодору, В следует из А, когда импликация А É В («если А, то В») необходима, так что нельзя утверждать в зависимости от случая, что иной раз она истинна, а иной раз нет, если А и В одни и те же высказывания. Филон же полагал, что понятие «В следует из А» полностью определяется понятием материальной импликации, которую он ввёл, дав свод её истинностных значений. Так возникла теория критериев логического следования, впоследствии сделавшаяся частью учения стоиков. Неизвестно, обсуждался ли в мегарской школе вопрос об аксиоматизации Л., но Диоген Лаэрций свидетельствует, что Клитомах из школы Евклида был первым, кто написал не дошедший до нас трактат об аксиомах и предикатах.
Логические идеи мегариков были ассимилированы в философской школе стоиков, основанной около 300 до н. э. Гл. фигурой этой школы был Хрисипп, принявший критерий Филона для импликации и двузначности принцип как онтологическую предпосылку Л. В сочинениях стоиков Л. высказываний предшествует аристотелевской силлогистике, оформляясь в систему правил построения и правил вывода высказываний. Последние по примеру Аристотеля тоже называются силлогизмами. Идея дедукции формулируется более четко, чем у мегариков, в виде след. предписания: условием формальной правильности заключения В из посылок А1, А2,..., An является истинность импликации (A1 & A2 &... & An) É В. Аргументы, основанные на понимании высказываний только как функций истинности, стоики называли формальными; они могут вести от ложных посылок к истинным следствиям. Если же во внимание принималась содержательная истинность посылок, формальные аргументы назывались истинными. Если посылки и заключения в истинных аргументах относились соответственно как причины и следствия, аргументы называются доказывающими. В общем случае «доказывающие аргументы» стоиков предполагали понятие о естественных законах. Стоики считали их аналитическими и возможность их доказательства посредством аналогии и индукции отрицали. Т. о., развитое стоиками учение о доказательстве шло за пределы Л. в область теории познания, и именно здесь «дедуктивизм» стоиков нашёл себе философского противника в лице радикального эмпиризма школы Эпикура — последней наиболее важной для истории Л. школы античности. В споре со стоиками эпикурейцы защищали опыт, аналогию, индукцию. Они положили начало индуктивной Л., указав, в частности, на роль противоречащего примера в проблеме обоснования индукции и сформулировав ряд правил индуктивного обобщения.
Эпикурейской «каноникой» заканчивается история логической мысли ранней античности. На смену приходит поздняя античность, эклектически сочетающая аристотелизм и стоицизм. Её вклад в Л. ограничивается по существу переводческой и комментаторской деятельностью поздних перипатетиков (Боэт Сидонский, Александр Эгский, Адраст, Гермин, Александр Афродизийский, Гален и др.) и неоплатоников (Порфирий, Прокл, Симпликий, Марий Викторин, Апулей, Августин, Боэций, Кассиодор и др.). Из нововведений эллино-римских логиков заслуживают внимания логический квадрат Апулея, дихотомическое деление и объёмная трактовка терминов силлогизма у Порфирия, идеи аксиоматизации Л. и Л. отношений у Галена, зачатки истории Л. у Секста Эмпирика и Диогена Лаэрция, наконец, подготовившие терминологию средневековой Л. переводы греческих текстов на латинский язык, в частности «Введения» Порфирия Марием Викторином и сочинений Аристотеля, входящих в «Органон», Боэцием. (Именно в логическом словаре Боэция впервые, по-видимому, появляются понятия «субъект», «предикат», «связка», в терминах которых на протяжении многих последующих столетий логики анализировали высказывания.) Под влиянием доктрины стоиков, заимствованной неоплатонизмом, Л. постепенно сближается с грамматикой. В энциклопедии той эпохи — «Сатириконе» Марциана Капеллы — в качестве одного из семи свободных искусств Л. объявляется необходимым элементом гуманитарного образования.
Логическая мысль раннего европейского средневековья (7—11 вв.), усваивавшего научное наследие античного мира сквозь призму христианского сознания, в творческом отношении значительно беднее эллиноримской. Как самостоятельная наука Л. развивается лишь в странах арабской культуры, где философия остаётся относительно независимой от религии. В Европе же складывается в основном схоластическая Л. в собственном смысле — церковно-школьная дисциплина, приспособившая элементы перипатетической Л. к нуждам обоснования и систематизации христианского вероучения. Лишь в 12—13 вв., после того как все произведения Аристотеля канонизируются церковной ортодоксией, возникает оригинальная средневековая («несхоластическая») Л., известная под назв. logica modernorum. Контуры её намечены уже «Диалектикой» Абеляра, но окончательное оформление она получает к конце 13 — середине 14 вв. в работах Уильяма Шервуда, Петра Испанского, Иоанна Дунса Скота, Вальтера Бурлея (Бёрли), Уильяма Оккама, Жана Буридана и Альберта Саксонского. В сочинениях этих авторов впервые прослеживаются прообраз «универсума речи» и представление о двояком использовании языка: для выражения мысли о внеязыковых фактах, когда термины «употребляются», и для выражения мысли о самом языке, когда термины «упоминаются» (употребляются автонимно). Учение о пропозициональных связках и кванторах, символизирующих характер логической связи, служит им естественным основанием для различения между «формой» и «содержанием» суждений. А в связи с задачей однозначного «прочтения» синтаксической структуры суждения средневековой логики неявно используют и понятие «области действия» логических операций. Их учение о «следовании» основывается на различии между материальной импликацией и формальной, или тавтологичной, импликацией: для первой можно указать контрпример, для второй — нет. Поэтому материальная импликация рассматривается как выражение содержательного, или фактического, следования, а формальная — логического. Средневековые логики открыли многие известные теперь законы Л. высказываний, которая составляла основу их теории дедукции и которая, как и у стоиков, считалась более общей, чем аристотелевская силлогистика. В этот же период впервые зародилась идея машинизации процесса логического вывода и были предприняты первые попытки её реализации (Р. Луллий).
Последующие два столетия — эпоха Возрождения — для дедуктивной Л. были эпохой кризиса. Её воспринимали как опору мыслительных привычек схоластики, как Л. «искусственного мышления», освящающую схематизм умозаключений, в которых посылки устанавливаются авторитетом веры, а не познания. Руководствуясь общим лозунгом эпохи: «вместо абстракций — опыт», дедуктивной Л. стали противопоставлять Л. «естественного мышления», под которой обычно подразумевались интуиция и воображение. Леонардо да Винчи и Ф. Бэкон переоткрывают античную идею индукции и индуктивного метода, выступая с резкой критикой силлогизма. И лишь немногие, подобно падуанцу Я. Дзабарелле (16 в.), пробуют вернуть в методологию научной мысли традиционную логическую дедукцию, предварительно освободив её от схоластической философской интерпретации.
Книги Дзабареллы оказали заметное влияние на положение Л. в 17 в. Уже у Т. Гоббса и П. Гассенди дедуктивная Л. полностью освобождается от связи с теологией и перипатетической философией. Несколько раньше основатель точного естествознания Г. Галилей восстанавливает права абстракции. Он обосновывает потребность в абстракциях, которые бы «восполняли» данные опытных наблюдений, и указывает на необходимость введения этих абстракций в систему дедукции в качестве гипотез, или постулатов, или аксиом, с последующим сравнением результатов дедукции с результатами наблюдений. Критицизм в отношении схоластики и одновременная реабилитация дедукции, правда, при некотором снижении интереса к формальной стороне доказательств, характерны для картезианской, т. е. опирающейся на методологические идеи Р. Декарта, логики, систематически изложенной в сочинении А. Арно и П. Николя «Логика, или Искусство мыслить» (1662), вошедшей в историю под названием логики Пор-Рояля. В этой книге Л. представлена как рабочий инструмент всех др. наук и практики, поскольку она принуждает к строгим формулировкам мысли.
Картезианская идея mathesis universalis стала ведущей в Л. середины 17 — начале 18 вв. Особое место в её развитии принадлежит Г. В. Лейбницу. Вслед за Р. Декартом, Т. Гоббсом и логиками Пор-Рояля Лейбниц считал возможным создать «всеобщую символику», своеобразный искусственный язык, который был бы свободен от многозначностей, присущих естественным разговорным языкам, понимался без словаря и был бы способен точно и однозначно выражать мысли. Такой язык мог бы играть роль вспомогательного международного языка, а также служить орудием открытия новых истин из известных. Анализируя категории Аристотеля, Лейбниц пришёл к идее выделения простейших исходных понятий и суждений, которые могли бы составить «алфавит человеческих мыслей»; эти первичные неопределяемые понятия, скомбинированные по определённым правилам, должны давать все остальные точно определимые понятия. Лейбниц полагал, что одновременно с таким анализом понятий можно создать универсальный алгоритм, который позволит провести доказательство всех известных истин и составить тем самым «доказательную энциклопедию».
С целью реализации этого замысла Лейбниц дал несколько вариантов арифметизации логики. В одном из них каждому исходному понятию сопоставляется простое число, каждому составному — произведение простых чисел, сопоставленных исходным понятиям, образующим данное составное (эта замечательная по своей простоте идея сыграла впоследствии исключительно важную роль в математике и логике благодаря работам Г. Кантора и К. Гёделя).
К Лейбницу же восходят многие методологически важные фрагменты современной Л. Так, большое значение он придавал проблеме тождества. Принимая схоластический принцип индивидуации (принцип «внутреннего различия»), положенный им в основу монадологии, Лейбниц отказался от онтологизации тождества, определяя тождество через сохраняющую истинность взаимозаменимость в контексте и намечая тем самым путь к построению теорий тождества, основанных на абстракции отождествления.
Хотя Лейбниц непосредственно не занимался индуктивной Л., соответствующая проблематика вполне им учитывалась. В частности, она нашла отражение в проводившемся им различении «истин разума» и «истин факта»; для проверки истин разума, по Лейбницу, достаточно законов аристотелевской Л.; для проверки истин факта, т. е. эмпирических истин, нужен ещё (сформулированный Лейбницем) достаточного основания принцип. В связи с этим Лейбниц рассматривал поставленную Галилеем проблему подтверждения общих суждений о действительности эмпирическими фактами, явившись тем самым одним из создателей теории т. н. гипотетико-дедуктивного метода.
Исходным пунктом индуктивной Л. нового времени служили методологические идеи Бэкона, но систематически эта логика — Л., исследующая «обобщающие выводы» как заключения, основанные на установлении причинной связи (см. Причинность) между явлениями, — была разработана Дж. С. Миллем (1843), который опирался, в свою очередь, на идеи Дж. Гершеля. Развитая Миллем теория индуктивных умозаключений стала предметом разработки и критики как в Л. 19 в., так и в Л. 20 в. (в частности, в работах русских логиков М. И. Каринского и Л. Б. Рутковского и статистика А. А. Чупрова). При этом она была поставлена в связь с проблематикой теории вероятностей, с одной стороны, и алгебры логики — с другой (начиная уже с работ У. С. Джевонса). Индуктивная Л. 19 в., центральным вопросом которой был вопрос о способах обоснования эмпирических заключений о закономерных (регулярных) связях явлений, в 20 в., с одной стороны, трансформировалась в вероятностную логику, а с другой — вышла за пределы Л. в собственном смысле, приобретя в существенно обогащённом виде новую жизнь в современной математической статистике и теории планирования эксперимента.
Индуктивная Л. не была, однако, главной линией развития логической мысли. Этой линией стало развитие строго дедуктивной — математической — логики, истоки которой были заключены уже в сочинениях Лейбница. Хотя большая часть логического наследия последнего оставалась неопубликованной до начала 20 в., прижизненное распространение его идей оказало заметное влияние на развитие алгебрологических методов в Л., в процессе которого уже в 19 в. в трудах О. де Моргана, Дж. Буля, немецкого математика Э. Шрёдера, П. С. Порецкого и др. путём применения математического (в основном алгебраического) метода к Л. была построена развитая логическая теория алгебраического характера, на основе которой в дальнейшем сформировалась современная алгебра Л.
Центральной фигурой этого «алгебро-логического» этапа в истории Л. был Буль. Он разработал свою алгебру Л. (термин «алгебра логики» был введён после Буля Ч. Пирсом) как обычную для того времени алгебру, а не как дедуктивную систему в позднейшем смысле. Не удивительно, что Буль стремился сохранить в своей алгебре Л. все арифметические операции, в том числе вычитание и деление, которые оказалось трудно истолковать логически. Алгебра логики Буля (интерпретировавшаяся прежде всего как логика классов, т. е. объёмов понятий) была значительно упрощена и усовершенствована Джевонсом, отказавшимся в Л. от операций вычитания и деления. У Джевонса мы уже встречаем ту алгебраическую систему, которая впоследствии получила название «булевой алгебры» (у самого Буля, использовавшего в своей алгебре операцию, соответствующую исключающему логическому союзу «или», т. е. строгую дизъюнкцию, а не распространённую в современной Л. «обычную», слабую, дизъюнкцию, «булевой алгебры» непосредственно не было). Строгие методы решения логических уравнений были предложены Шрёдером (1877) и Порецким (1884). Многотомные «Лекции по алгебре логики» (1890—1905) Шрёдера (вместе с работами Порецкого вплоть до 1907) явились высшей точкой развития алгебры Л. 19 в.
История алгебры Л. началась с попыток перенести в Л. все операции и законы арифметики, но постепенно логики начинали сомневаться не только в правомерности, но и в целесообразности такого переноса. Они выработали специфические именно для Л. операции и законы. Наряду с алгебраическими в Л. издавна применялись геометрические (точнее, графические) методы. Приёмами представления модусов силлогизмов с помощью геометрических фигур владели античные комментаторы Аристотеля. Использование с этой целью кругов, обычно приписываемое Л. Эйлеру, было известно ещё И. К. Штурму (1661) и Лейбницу, владевшему и отличными от эйлеровых методами. Способы геометрической интерпретации предложений Л. имелись у И. Г. Ламберта и Б. Больцано. Но особенного расцвета эти методы достигли в трудах Дж. Венна, разработавшего графический аппарат диаграмм (см. Логические диаграммы.), фактически полностью эквивалентный Л. классов и носящий уже не только иллюстративный, но и эвристический характер.
К концу 19 в. в дедуктивной Л. произошёл глубокий переворот, связанный с работами Дж. Пеано, Пирса и Г. Фреге, которые преодолели узость чисто алгебраического подхода прежних авторов, осознали значение математической Л. для математиков и начали применять её к вопросам оснований арифметики и теории множеств. Достижения этого периода, в особенности связанные с аксиоматическим построением Л., в наиболее чёткой форме можно проследить в исследованиях Фреге. Начиная со своей работы «Исчисление понятий» (1879), он развил совершенно строгое аксиоматическое построение исчисления высказываний и предикатов. Его формализованная Л. содержала все основные элементы современных логических исчислений: пропозициональные переменные (переменные для высказываний), предметные переменные, кванторы (для которых он ввёл специальные символы) и предикаты; он подчёркивал различие между логическими законами и правилами логического вывода, между переменной и константой, различал (не вводя, правда, особых терминов) язык и метаязык (см. Метатеория, Метаязык). Его исследования (так же как аналогичные работы Пирса) в области логической структуры естественного языка и семантики логических исчислений положили начало проблемам логической семантики. Большой заслугой Фреге явилась разработка системы формализованной арифметики, основанной на развитой им логике предикатов. Эти работы Фреге и выявившиеся в связи с ними трудности послужили исходным пунктом развития современной теории математического доказательства.
Фреге употреблял оригинальную символику, которая, в отличие от обычно применяемой одномерной, была двумерной (она не привилась). Современная система обозначений в Л. восходит к символике, предложенной Дж. Пеано. С некоторыми изменениями она была воспринята Б. Расселом, создавшим совместно с А. Н. Уайтхедом трёхтомный труд «Принципы математики» — труд, систематизировавший и развивший далее дедуктивно-аксиоматическое построение Л. в целях логического обоснования математического анализа (см. Логицизм).
С этого сочинения и начавших появляться с 1904 работ Д. Гильберта по математической Л. естественно датировать начало современного этапа логических исследований.
М. М. Новосёлов, 3. А. Кузичева, Б. В. Бирюков.
Предмет и метод современной логики. Современная Л. развилась в точную науку, применяющую математические методы. Она стала, по словам Порецкого, математической логикой — Л. по предмету, математикой по методу. В этом качестве Л. стала пригодной для правильной постановки и решения логических проблем математики, в особенности проблем, связанных с доказуемостью и недоказуемостью тех или иных положений математических теорий. Точная постановка таких проблем требует прежде всего уточнения понятия доказательства. Всякое математическое доказательство состоит в последовательном применении тех или иных логических средств к исходным положениям. Но логические средства не представляют собой чего-то абсолютного, раз навсегда установленного. Они вырабатывались в процессе многовековой человеческой практики; «... практическая деятельность человека миллиарды раз должна была приводить сознание человека к повторению разных логических фигур, дабы эти фигуры могли получить значение аксиом» (Ленин В. И., Полн. собр. соч., 5 изд., т. 29, с. 172). Человеческая практика является, однако, на каждом историческом этапе ограниченной, а объём её всё время растёт. Логические средства, удовлетворительно отражавшие практику человеческого мышления на данном этапе или в данной области, могут оказаться неподходящими на следующем этапе или в другой области. Тогда в зависимости от изменения содержания рассматриваемого предмета изменяется и способ его рассмотрения — изменяются логические средства. Это в особенности относится к математике с её далеко идущими многократными абстракциями. Здесь совершенно бессмысленно говорить о логических средствах как о чём-то данном в своей совокупности, как о чём-то абсолютном. Зато имеет смысл рассмотрение логических средств, применяемых в той или иной конкретной обстановке, встречающейся в математике. Их установление для какой-либо данной математической теории и составляет искомое уточнение понятия доказательства применительно к этой теории. Важность этого уточнения для развития математики выявилась в особенности в связи с проблемами её оснований. Разрабатывая множеств теорию, исследователи столкнулись с рядом своеобразных трудных проблем. Исторически первой из них явилась проблема о мощности континуума, выдвинутая Кантором (1883), к которой до 1939 не было найдено подходов (см. Континуума проблема). Другие проблемы, столь же упорно не поддававшиеся решению, встретились в т. н. дескриптивной теории множеств, успешно разрабатываемой советскими математиками. Постепенно становилось всё более ясно, что трудность этих проблем имеет логическую природу, что эта трудность обусловлена неполной выявленностью применяемых логических средств и что единственным путём к её преодолению является уточнение этих средств. Выяснилось, т. о., что разрешение этих задач требует привлечения новой математической науки — математической логики. Надежды, возлагавшиеся на математическую Л. в связи с этими проблемами, оправдались. В особенности это касается проблемы континуума, которая может считаться полностью решённой благодаря работам К. Гёделя (1939) и П. Коэна (1963). Первый из них доказал совместимость обобщённой континуум-гипотезы Кантора с аксиомами теории множеств в предположении непротиворечивости последних. Второй при том же предположении доказал независимость континуум-гипотезы от аксиом теории множеств, т. е. её недоказуемость. Аналогичные результаты были получены П. С. Новиковым (1951) в отношении ряда проблем дескриптивной теории множеств. Уточнение понятия доказательства в математической теории путём установления допускаемых логических средств является существенным этапом её развития. Теории, прошедшие этот этап, называются дедуктивными теориями. Лишь для них допускают точную формулировку интересующие математиков проблемы доказуемости и непротиворечивости.
Для решения этих проблем в современной Л. применяется метод формализации доказательств — один из основных её методов. Сущность его состоит в следующем.
Формулировки теорем и аксиом развиваемой теории полностью записываются в виде формул, для чего употребляется особая символика, пользующаяся, наряду с обычными математическими знаками, знаками для логических связок, применяемых в математике: «... и...», «... или...», «если..., то...», «неверно, что...», «при всяком...», «существует... такой, что...». Всем логическим средствам, с помощью которых теоремы выводятся из аксиом, ставятся в соответствие правила вывода новых формул из уже выведенных. Эти правила формальны, т. е. таковы, что для проверки правильности их применений нет надобности вникать в смысл формул, к которым они применяются, и формулы, получаемой в результате; надо лишь убедиться, что эти формулы построены из таких-то знаков, так-то расположенных. Доказательство теоремы отображается в выводе выражающей её формулы. Вывод же этот рассматривается как ряд формул, в конце которого стоит формула, подлежащая выводу. В выводе всякая формула либо выражает аксиому, либо получается из одной или нескольких предыдущих формул по одному из правил вывода. Формула считается выводимой, если может быть построен её вывод.
Если сопоставление правил вывода применяемым логическим средствам было произведено надлежащим образом, то получают возможность судить о доказуемости теорем в данной теории по выводимости выражающих их формул. Выяснение выводимости или невыводимости той или иной формулы есть задача, не требующая привлечения далеко идущих абстракций, и решать эту задачу часто бывает возможно сравнительно элементарными методами.
Идея метода формализации доказательств принадлежит Д. Гильберту. Проведение этой идеи стало, однако, возможным благодаря предшествовавшей разработке математической Л. (см. раздел История логики).
Применение идеи формализации доказательств бывает обычно связано с выделением логической части рассматриваемой дедуктивной теории. Эта логическая часть, оформляемая, как и вся теория, в виде некоторого исчисления, т. е. системы формализованных аксиом и формальных правил вывода, может тогда рассматриваться как самостоятельное целое.
Простейшими из логических исчислений являются исчисления высказываний: классическое и интуиционистское. В них употребляются следующие знаки: 1) т. н. логические переменные — буквы А, В, С,..., означающие произвольные «высказывания» (смысл этого термина объясняется ниже); 2) знаки логических связок &, 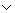 , É, ù, означающие соответственно «... и...», «... или...», «если..., то...», «неверно, что...»; 3) скобки, выявляющие строение формул. Формулами в этих исчислениях считаются логические переменные и всякие выражения, получаемые из них путём повторного применения следующих операций: 1) присоединение к ранее построенному выражению знака ù слева, 2) написание двух ранее построенных выражений рядом друг за другом со включением одного из знаков &,
, É, ù, означающие соответственно «... и...», «... или...», «если..., то...», «неверно, что...»; 3) скобки, выявляющие строение формул. Формулами в этих исчислениях считаются логические переменные и всякие выражения, получаемые из них путём повторного применения следующих операций: 1) присоединение к ранее построенному выражению знака ù слева, 2) написание двух ранее построенных выражений рядом друг за другом со включением одного из знаков &,  или É между ними и с заключением всего в скобки. Например, следующие выражения являются формулами:
или É между ними и с заключением всего в скобки. Например, следующие выражения являются формулами:
1. (АÉ(ВÉА)),
2. ((АÉ(ВÉС)) É((АÉВ) É(АÉС))),
3. ((A&B) ÉA),
4. ((А&. В) ÉВ),
5. (AÉ(BÉ(A&B))),
6. ((АÉС) É((ВÉС) É((А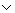 В) ÉС))),
В) ÉС))),
7. (АÉ(А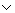 В)),
В)),
8. (BÉ(A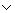 B)),
B)),
9. (ùАÉ(АÉВ)),
10. ((AÉB) É((AÉùB) ÉùA)),
11. (A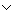 ùA).
ùA).
В обоих исчислениях высказываний — классическом и интуиционистском — употребляются одни и те же правила вывода.
Правило подстановки. Из формулы выводится новая формула путём подстановки всюду вместо какой-либо логической переменной произвольной формулы.
Правило вывода заключений. Из формул  и (
и (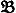 ) выводится формула
) выводится формула 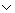 Q), называется дизъюнкцией суждений Р и Q, есть суждение истинное, когда истинно хотя бы одно из этих суждений, и ложное, когда ложны оба. Суждение вида (Р É Q), называется импликацией суждений Р и Q, есть суждение ложное, когда истинно Р и ложно Q, и истинное во всех остальных случаях. Суждение вида ù Р, называется отрицанием суждения Р, есть суждение истинное, когда Р ложно, и ложное, когда Р истинно.
Q), называется дизъюнкцией суждений Р и Q, есть суждение истинное, когда истинно хотя бы одно из этих суждений, и ложное, когда ложны оба. Суждение вида (Р É Q), называется импликацией суждений Р и Q, есть суждение ложное, когда истинно Р и ложно Q, и истинное во всех остальных случаях. Суждение вида ù Р, называется отрицанием суждения Р, есть суждение истинное, когда Р ложно, и ложное, когда Р истинно.
Необходимо отметить, что, согласно данному выше определению, импликация не вполне совпадает по смыслу с житейским словоупотреблением связки «если..., то...». Однако в математике эта связка обычно применялась именно в смысле этого определения импликации. Доказывая теорему вида «если Р, то Q», где Р и Q суть некоторые математические суждения, математик делает предположение об истинности Р и тогда доказывает истинность Q. Он продолжает считать теорему верной, если впоследствии будет доказана ложность Р или истинность Q будет доказана и без предположения об истинности Р. Опровергнутой он считает эту теорему лишь тогда, когда установлена истинность Р и вместе с тем ложность Q. Всё это вполне согласуется с определением импликации (Р É Q).
Необходимо также подчеркнуть принятое в математической Л. неисключающее понимание дизъюнкции. Дизъюнкция (Р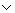 Q), по определению, истинна и в том случае, когда истинны оба суждения Р и Q.
Q), по определению, истинна и в том случае, когда истинны оба суждения Р и Q.
Формула 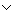 В) можно утверждать тогда и только тогда, когда можно утверждать хотя бы одно из высказываний А и В. Отрицание ùА высказывания А можно утверждать тогда и только тогда, когда у нас есть построение, приводящее к противоречию предположение о том, что построение, требуемое высказыванием А, выполнено. (При этом «приведение к противоречию» считается первоначальным понятием.) Импликацию (АÉВ) можно утверждать тогда и только тогда, когда мы располагаем таким построением, которое, будучи объединено с любым построением, требуемым высказыванием А, даёт построение, требуемое высказыванием В.
В) можно утверждать тогда и только тогда, когда можно утверждать хотя бы одно из высказываний А и В. Отрицание ùА высказывания А можно утверждать тогда и только тогда, когда у нас есть построение, приводящее к противоречию предположение о том, что построение, требуемое высказыванием А, выполнено. (При этом «приведение к противоречию» считается первоначальным понятием.) Импликацию (АÉВ) можно утверждать тогда и только тогда, когда мы располагаем таким построением, которое, будучи объединено с любым построением, требуемым высказыванием А, даёт построение, требуемое высказыванием В.
Формула называется интуиционистски общезначимой тогда и только тогда, когда можно утверждать всякое высказывание, получаемое из в результате подстановки любых математических суждений вместо логических переменных; точнее говоря, в том случае, когда имеется общий метод, позволяющий при произвольной такой подстановке получать построение, требуемое результатом подстановки. При этом понятие общего метода интуиционисты также считают первоначальным.
Формулы 1—10 являются интуиционистски общезначимыми, тогда как формула 11, выражающая классический закон исключенного третьего, не является таковой.
В известном отношении близкой к интуиционизму является точка зрения конструктивной математики, уточняющая несколько расплывчатые интуиционистские понятия импликации и общего метода на основе точного понятия алгоритма. С этой точки зрения закон исключенного третьего также отвергается. Л. конструктивной математики находится в стадии разработки.
С методом формализации доказательств связано понятие формальной системы. Формальная система включает следующие элементы.
1. Формализованный язык с точным синтаксисом, состоящий из точных и формальных правил построения осмысленных выражений, называется формулами данного языка.
2. Чёткую семантику этого языка, состоящую из соглашений, определяющих понимание формул и тем самым условия их истинности.
3. Исчисление (см. выше), состоящее из формализованных аксиом и формальных правил вывода. При наличии семантики эти правила должны быть согласованы с ней, т. е. при применении к верным формулам давать верные формулы.
Исчисление определяет выводы (см. выше) и выводимые формулы — заключительные формулы выводов. Для выводов имеется распознающий алгоритм — единый общий метод, с помощью которого для любой цепочки знаков, применяемых в исчислении, можно узнавать, является ли она выводом. Для выводимых формул распознающий алгоритм может быть и невозможен (примером является исчисление предикатов, см. Логика предикатов).
Об исчислении говорят, что оно непротиворечиво, если в нём не выводима никакая формула вместе с формулой ù. Задача установления непротиворечивости применяемых в математике исчислений является одной из главных задач математической Л. Имея в виду охват той или иной содержательно определённой области математики, исчисление считают полным относительно этой области, если в нём выводима всякая формула, выражающая верное утверждение из этой области. Другое понятие полноты исчисления связано с требованием иметь для всякого утверждения, формулируемого в данном исчислении, либо его доказательство, либо его опровержение. Первостепенное значение в связи с этими понятиями имеет теорема Гёделя, утверждающая несовместимость требований полноты с требованием непротиворечивости для весьма широкого класса исчислений. Согласно теореме Гёделя, никакое непротиворечивое исчисление из этого класса не может быть полным относительно арифметики: для всякого такого исчисления может быть построено верное арифметическое утверждение, формализуемое, но не выводимое в исчислении. Эта теорема, не снижая значения математической Л. как мощного организующего средства в науке, убивает надежды на эту дисциплину как на нечто способное осуществить охват математики в рамках одной формальной системы. Надежды такого рода высказывались многими учёными, в том числе основоположником математического формализма Гильбертом.
В 70-е гг. 20 в. получила развитие идея полуформальной системы. Полуформальная система — это также система некоторых правил вывода. Однако некоторые из этих правил могут иметь существенно иной характер, чем правила вывода формальной системы. Они, например, могут допускать выведение новой формулы после того, как с помощью интуиции создалось убеждение в выводимости любой формулы такого-то вида. Сочетание этой идеи с идеей ступенчатого построения математической Л. лежит в основе одного из современных построений логики конструктивной математики. В приложениях математической Л. часто применяются исчисления предикатов — классическое и интуиционистское.
Математическая Л. органически связана с кибернетикой, в частности с математической теорией управляющих систем и математической лингвистикой. Приложения математической Л. к релейно-контактным схемам основаны на том, что всякая двухполюсная релейно-контактная схема в следующем смысле моделирует некоторую формулу классического исчисления высказываний. Если схема управляется n реле, то столько же различных пропозициональных переменных содержит , и если обозначить через i суждение «Реле номер i сработало», то цепь будет тогда и только тогда замкнута, когда будет верен результат подстановки суждений i вместо соответствующих логических переменных в . Построение такой моделируемой формулы, описывающей «условия работы» схемы, оказывается особенно простым для т. н. П-схем, получаемых из элементарных одноконтактных цепей путём параллельных и последовательных соединений. Это связано с тем, что параллельные и последовательные соединения цепей моделируют соответственно дизъюнкцию и конъюнкцию суждений. Действительно, цепь, полученная путём параллельного (последовательного) соединения цепей Ц1 и Ц2, тогда и только тогда замкнута, когда замкнута цепь Ц1 или (и) замкнута цепь Ц2. Применение исчисления высказываний к релейно-контактным схемам открыло плодотворный подход к важным проблемам современной техники. Это же применение обусловило постановку и частичное решение многих новых и трудных проблем математической Л., к числу которых в первую очередь относится т. н. проблема минимизации, состоящая в разыскании эффективных методов нахождения простейшей формулы, равносильной данной формуле.
Релейно-контактные схемы являются частным случаем управляющих схем, применяемых в современных автоматах. Управляющие схемы иных типов, в частности схемы из электронных ламп или полупроводниковых элементов, имеющие ещё большее практическое значение, также могут быть разрабатываемы с помощью математической Л., которая доставляет адекватные средства как для анализа, так и для синтеза таких схем. Язык математической Л. оказался также применимым в теории программирования, создаваемой в связи с развитием машинной математики. Наконец, созданный математической Л. аппарат исчислений оказался применимым в математической лингвистике, изучающей язык математическими методами.
А. А. Марков.
Научные учреждения и издания. Преподавание и исследовательская работа по Л. являются неотъемлемой частью научной и культурной жизни большинства стран мира. В СССР научно-исследовательская работа в области Л. ведётся в основном в научно-исследовательских центрах Москвы, Ленинграда, Новосибирска, Киева, Кишинева, Риги, Вильнюса, Тбилиси, Еревана и др. городов отделениями математических институтов АН СССР и союзных республик, институтами философии, кафедрами Л. университетов и некоторых др. вузов. Публикации работ по Л. в СССР осуществляются: в непериодических изданиях в форме тематических сборников и монографий (в частности, начиная с 1959 в серии «Математическая логика и основания математики»), в непериодических изданиях «Трудов Математического института им. В. А. Стеклова АН СССР» (с 1931), в сборниках «Алгебра и логика» (Новосибирск, с 1962), в «Записках» научных семинаров по Л., в математических и философских журналах. В реферативном журнале «Математика» и в реферативных журналах института научной информации по общественным наукам АН СССР систематически освещаются работы советских и зарубежных авторов по Л. Из специальных зарубежных изданий, освещающих проблематику Л., наиболее известны: международная монографическая серия «Studies in Logic...» (Amst., с 1965) и журналы: «The Journal of Symbolic Logic» (Providence, с 1936); «Zeitschrift für mathematische Logik und Grundlagen der Mathematik» (В., с 1955); «Archiv für mathematische Logik und Grundlagenforschung» (Stuttg., с 1950); «Logique et analyse» (Louvain, с 1958); «Journal of philosophical logic» (Dordrecht, с 1972); «International logic review» (Bologna, с 1970); «Studia Logica» (Warsz., с 1953); «Notre Dame Journal of formal Logic» (Notre Dame, с 1960).
Основную организационную работу, связанную с обменом научной информацией в области Л., осуществляет пользующаяся поддержкой ООН Ассоциация символической логики. Ассоциация организует международные конгрессы по Л., методологии и философии науки. Первый такой конгресс состоялся в 1960 в Станфорде (США), второй — в 1964 в Иерусалиме, третий — в 1967 в Амстердаме, четвёртый — в 1971 в Бухаресте.
З. А. Кузичева, М. М. Новосёлов.
Лит.: Основные классические работы. Аристотель, Аналитики первая и: вторая, пер. с греч., М., 1952; Leibniz G. W., Fragmente zur Logik, В., 1960; Кант И., Логика, пер. с нем., П., 1915; Милль Дж. С., Система логики силлогистической и индуктивной, пер. с англ., 2 изд., М., 1914; De Morgan A., Formal logic or the calculus of inference, necessary and probable, L., 1847 (перепечатка, L., 1926); Boole G., The mathematical analysis of logic, being an essay toward a calculus of deductive reasoning, L. — Camb., 1847 (перепечатка, N. Y., 1965); Schröder Е., Der Operationskreis des Logikkalkuls, Lpz., 1877; Frege G., Begriffsschrift, eine der arithmetischen nachgebildete Formelsprache des reinen Denkens, Halle, 1879; Джевонс С., Основы науки, Трактат о логике и научном методе, пер. с англ., СПБ, 1881; Порецкий П. С., О способах решения логических равенств и об обратном способе математической логики, Казань, 1884; Whitehead A. N., Russell B., Principia mathematica, 2 ed., v. 1—3, Camb., 1925—27.
История. Владиславлев М., Логика, СПБ, 1872 (см. «Приложение»); Троицкий М., Учебник логики с подробным указанием на историю и современное состояние этой науки в России и в других странах, т. 1—3, М., 1885—88; Яновская С. А., Основания математики и математическая логика, в кн.: Математика в СССР за тридцать лет, М. — Л., 1948; её же, Математическая логика и основания математики, в кн.: Математика в СССР за сорок лет, т. 1, М., 1959; Попов П. С., История логики нового времени, М., 1960; Котарбиньский Т., Лекции по истории логики, Избр. произв., пер. с польск., М., 1963, с. 353—606; Стяжкин Н. И., Формирование математической логики, М., 1967; Prantl К., Geschichte der Logik im Abendlande, Bd 1—4, Lpz., 1855—70; Bochenski I. М., Formale Logik, Münch., 1956; Minio Paluello L., Twelfth century logic. Texts and Studies, v. 1—2, Roma, 1956—58; Scholz Н., Abriss der Geschichte der Logik, Freiburg — Münch., 1959; Lewis C. I., A survey of symbolic logic, N. Y., 1960; lørgensen J., A treatise of formal logic: Its evolution and main branches with its relation to mathematics and philosophy, v. 1—3, N. Y., 1962; Kneale W., Kneale М., The development of logic, 2 ed., Oxf., 1964; Dumitriu A., Istoria logicii, Buc., 1969; Blanché R., La logique et son histoire. D'Aristote a Russell, P., 1971; Berka K., Kreiser L., Logik — Texte. Kommentierte Auswahl zur Geschichte der modernen Logik, B., 1971.
Учебные курсы. Гильберт Д., Аккерман В., Основы теоретической логики, пер. с нем., М., 1947; Тарский А., Введение в логику и методологию дедуктивных наук, пер. с англ., М., 1948; Новиков П. С., Элементы математической логики, М., 1959; Чёрч А., Введение в математическую логику, пер. с англ., т. 1, М., 1960; Гудстейн Р. Л., Математическая логика, пер. с англ., М., 1961; Гжегорчик А., Популярная логика. Общедоступный очерк логики предложений, пер. с польск., М., 1965; Мендельсон Э., Введение в математическую логику, пер. с англ., М., 1971; Марков А. А., О логике конструктивной математики, М., 1972.
Некоторые монографии. Клини С. К., Введение в метаматематику, пер. с англ., М., 1957; Рейтинг А., Интуиционизм, пер. с англ., М., 1965; Карри Х. Б., Основания математической логики, пер. с англ., М., 1969; Hilbert D., Bernays P., Grundlagen der Mathematik, Bd 1—2, В., 1934—39; Markov A. A., Essai de construction d'une logique de la mathématique constructive, Brux., 1971.
Энциклопедии и словари. Философская энциклопедия, т. 1—5, М., 1960—70; Кондаков Н. И., Логический словарь, М., 1971; Encyclopedia of Philosophy. v. 1—8, N. Y., 1967; Mała encykiopedia Logiki, Wrocław — Warsz. — Krakόw, 1970.
Библиография. Примаковский А. П., Библиография по логике. Хронологический указатель произведений по вопросам логики, изданных на русском языке в СССР в 18—20 вв., М., 1955; Ивин А. А., Примаковский А. П., Зарубежная литература по проблемам логики (1960—1966), «Вопросы философии», 1968, № 2; Church A., A bibliography of symbolic logic, «The Journal of Symbolic Logic», 1936, v. 1, № 4; его же, Additions and corrections to «A bibliography of symbolic logic», там же, 1938, v. 3, № 4; Beth E. W., Symbolische Logik und Grundlegung der exakten Wissenschaften, Bern, 1948 (Bibliographische Einführung in das Studium der Philosophie, Bd 3); Brie G. A. de, Bibliographia Philosophica. 1934—1945, Bd 1—2, Brux., 1950—54; Küng G., Bibliography of soviet works in the field of mathematical logic and the foundations of mathematics, from 1917—1957, «Notre Dame Journal of Formal Locic», 1962, № 3; Hänggi J., Bibliographie der Sovjetischen Logik, Bd 2, Winterthur, 1971.
 ), наука о приемлемых способах рассуждения. Слово «Л.» в его современном употреблении многозначно, хотя и не столь богато смысловыми оттенками, как древнегреч. lógos, от которого оно происходит. В духе традиции с понятием Л. связываются три основных аспекта: онтологический — «Л. вещей», т. е. необходимая связь явлений объективного мира (Демокрит); гносеологический — «Л. знания», т. е. необходимая связь понятий, посредством которой познаётся «сущность и истина» (Платон), и демонстративный (доказательный), или собственно логический, — «Л. доказательств и опровержений», т. е. необходимая связь суждений (высказываний) в рассуждениях (умозаключениях), принудительная убедительность («общезначимость») которых вытекает только из формы этой связи безотносительно к тому, выражают эти суждения «сущность и истину» или нет (Аристотель). Первые два аспекта относятся к философии и диалектической логике, последний же аспект составляет собственно логику, или современную Л. (которую вслед за И. Кантом иногда называют формальной Л.).
), наука о приемлемых способах рассуждения. Слово «Л.» в его современном употреблении многозначно, хотя и не столь богато смысловыми оттенками, как древнегреч. lógos, от которого оно происходит. В духе традиции с понятием Л. связываются три основных аспекта: онтологический — «Л. вещей», т. е. необходимая связь явлений объективного мира (Демокрит); гносеологический — «Л. знания», т. е. необходимая связь понятий, посредством которой познаётся «сущность и истина» (Платон), и демонстративный (доказательный), или собственно логический, — «Л. доказательств и опровержений», т. е. необходимая связь суждений (высказываний) в рассуждениях (умозаключениях), принудительная убедительность («общезначимость») которых вытекает только из формы этой связи безотносительно к тому, выражают эти суждения «сущность и истину» или нет (Аристотель). Первые два аспекта относятся к философии и диалектической логике, последний же аспект составляет собственно логику, или современную Л. (которую вслед за И. Кантом иногда называют формальной Л.).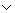 ,
,  или
или 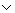 В)
В) 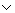 В)),
В)),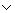 B)),
B)),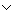
 и (
и (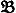 ) выводится формула
) выводится формула 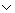 Q), называется дизъюнкцией суждений Р и Q, есть суждение истинное, когда истинно хотя бы одно из этих суждений, и ложное, когда ложны оба. Суждение вида (Р
Q), называется дизъюнкцией суждений Р и Q, есть суждение истинное, когда истинно хотя бы одно из этих суждений, и ложное, когда ложны оба. Суждение вида (Р 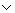 Q), по определению, истинна и в том случае, когда истинны оба суждения Р и Q.
Q), по определению, истинна и в том случае, когда истинны оба суждения Р и Q.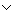 В) можно утверждать тогда и только тогда, когда можно утверждать хотя бы одно из высказываний А и В. Отрицание
В) можно утверждать тогда и только тогда, когда можно утверждать хотя бы одно из высказываний А и В. Отрицание