
Микроканонический ансамбль, статистический ансамбль для изолированных (не обменивающихся энергией с окружающими телами) макроскопических систем в постоянном объёме при постоянном числе частиц; энергия систем М. а. имеет строго постоянное значение. Понятие М. а., введённое Дж. У. Гиббсом в 1901, является идеализацией, т.к. в действительности полностью изолированных систем не существует.
В классической статистике статистический ансамбль характеризуется функцией распределения f (qi, pi), зависящей от координат qi и импульсов pi всех частиц системы. Эта функция определяет вероятность микроскопического состояния системы, т. е. вероятность того, что координаты и импульсы частиц системы имеют определённые значения. Согласно микроканоническому распределению Гиббса, все микроскопические состояния, отвечающие данной энергии, равновероятны. (Данная энергия системы может быть реализована при различных значениях координат и импульсов частиц системы.)
Если через H (qi, pi) обозначить энергию системы в зависимости от координат и импульсов (функцию Гамильтона), а через Е — заданное значение энергии, то
f (qi, pi) = A d{H (qi, pi) - E},
где d — дельта-функция Дирака, а постоянная А определяется условием нормировки (суммарная вероятность пребывания системы во всех возможных состояниях, определяемая интегралом от f (qi, pi) по всем qi, pi, равна 1) и зависит от объёма и энергии системы.
В квантовой статистике рассматривается ансамбль энергетически изолированных квантовых систем (с постоянным объёмом V и полным числом частиц N), имеющих одинаковую энергию E с точностью до DE << E. Предполагается, что для таких систем все квантовомеханические состояния с энергией Ek в слое E, E + DE равновероятны. Такое распределение вероятностей w состояний системы, когда

называется микроканоническим распределением. Здесь W(E, N, V) — статистический вес, определяемый из условия нормировки
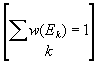
и равный числу квантовых состояний в слое E, E + DE. Величину DE выбирают обычно малой, но конечной (так как точная фиксация энергии в квантовой механике, в соответствии с неопределённостей соотношением между энергией и временем, потребовала бы бесконечного времени наблюдения). Однако М. а. малочувствителен к выбору ширины энергетического слоя DE, если она значительно меньше полной энергии системы. Поэтому в квантовой статистике можно также рассматривать ансамбль полностью изолированных систем, когда DE ® 0.
С помощью статистического веса W(E, N, V) можно вычислить энтропию S системы:
S = k lnW(E, N, V)
(k — Больцмана постоянная) и другие потенциалы термодинамические. Поскольку энтропия системы пропорциональна числу частиц N, статистический вес имеет порядок величины экспоненциальной функции от N и для рассматриваемых макроскопических систем очень велик.
Микроканоническое распределение неудобно для практического применения, т.к. для вычисления статистического веса нужно найти распределение квантовых уровней системы, состоящей из большого числа частиц, что представляет очень сложную задачу. Удобнее рассматривать не энергетически изолированные системы, а системы, находящиеся в тепловом контакте с окружающей средой, температура которой считается постоянной (с термостатом), и применять каноническое Гиббса распределение или рассматривать системы в тепловом и материальном контакте с термостатом (т. е. системы, для которых возможен обмен частицами и энергией с термостатом) и применять большое каноническое распределение Гиббса (см. Статистическая физика). Гиббс доказал теорему о том, что малая часть М. а. распределена канонически (теорема Гиббса). Эту теорему можно считать обоснованием канонического распределения Гиббса, если микроканоническое распределение принять как основной постулат статистической физики.
Лит. см. при ст. Статистическая физика.
Г. Я. Мякишев, Д. Н. Зубарев.