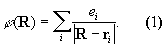
Мультиполь (от мульти... и греч. pólos — полюс), характеристика системы электрических зарядов («полюсов»), обладающей определённой симметрией. Создаваемое системой электромагнитное поле, статическое или переменное, на больших (по сравнению с размерами системы r) расстояниях R от системы можно представить как наложение полей М. различного порядка l (М. нулевого порядка — заряд, 1-го порядка — диполь, 2-го — квадруполь, 3-го — октуполь и т. д.). Для статических полей потенциал М. l-го порядка (2l-поля) убывает при R » r как 1/Rl+1 и обладает особой угловой зависимостью. Переменные (излучаемые) поля колеблющихся М. любого порядка на расстояниях R, много больших длины испускаемых волн (в волновой зоне), имеют одинаковую зависимость от R (меняются как 1/R) и различаются только угловой зависимостью, такой же, как и у статических М. Величина и угловое распределение поля М., а также энергия его взаимодействия с внешними полями определяются мультипольным моментом. Если все мультипольные моменты вплоть до порядка l – 1 равны нулю, то момент порядка l не зависит от выбора начала координат внутри системы.
В случае статической системы зарядов ei, расположенных в точках ri (с координатами xi (a = 1, 2, 3), потенциал j (R) постоянного электрического поля в точке R равен
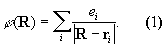
При больших R (R » ri,) потенциал можно представить в виде ряда по степеням ri/R:
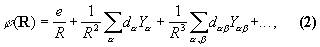
где скаляр
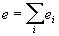
— полный заряд системы, вектор
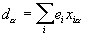
— её электрический дипольный момент, тензор
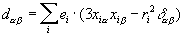
— квадрупольный момент (где a, b = 1, 2, 3, a dab — Кронекера символ, равный 1 при a = b и 0 при a ¹ b) и т. д., а величины Ya, Yab и т. д. зависят лишь от направления вектора R и выражаются через сферические функции соответствующего порядка l. В простейшем случае поле диполя создаётся двумя разноимёнными, одинаковыми по величине зарядами; поле квадруполя — четырьмя одинаковыми по величине зарядами, помещенными в вершины параллелограмма так, что каждая сторона соединяет разноимённые заряды; поле октуполя — восемью зарядами в вершинах параллелепипеда, когда каждое ребро соединяет разноимённые заряды, и т. д.
Магнитные М. применяются для описания магнитных свойств системы. Поскольку магнитных зарядов не существует, разложение для вектор-потенциала (см. Потенциалы электромагнитного поля), аналогичное разложению скалярного потенциала j, начинается с магнитного диполя.
Разложение по М. для переменного поля играет важную роль в классической теории излучения, теории антенн и т. п. Оно особенно полезно при квантовании поля излучения. Волновая функция поля излучения 2l-поля является собственной функцией оператора полного момента с собственным значением l: такой М. излучает фотоны только с моментом l.
Понятие «М.» применяется также для описания переменных акустического, гравитационного и др. полей.
Лит.: Ландау Л. Д., Лифшиц Е. М., Теория поля, 6 изд., М., 1973 (Теоретическая физика, т. 2); Френкель Я. И., Электродинамика, Собр. избр. трудов, т. 1, М. — Л., 1956; Ахиезер А. И., Берестецкий В. Б., Квантовая электродинамика, 3 изд., М., 1969.
В. П. Павлов.