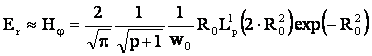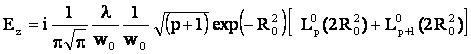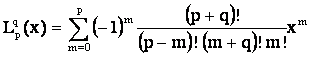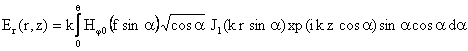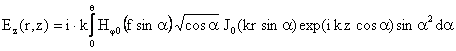Лазерные пучки с осесимметричным состоянием поляризации

Лазерные пучки с осесимметричным состоянием поляризации

Лазерные моды с радиальной и азимутальной поляризацией обладают уникальными свойствами и находят все большее применение в научных исследованиях и прикладных задачах. Основные достижения сотрудников ИПЛИТ РАН в этой области: Дано физически и математически корректное теоретическое описание. Разработан метод их генерации на основе интерферометра Саньяка для маломощных лазеров. Осуществлена генерация мод с R и A поляризацией в мощном СО2 лазере с помощью дифракционных зеркал и аксиконов. Теоретически рекомендовано использование этих мод в лазерной обработке материалов. Показана эффективность использования таких мод в качестве ловушек для холодных атомов. Разработан поляризационный микрозонд для диагностики биомолекул. Проведены расчеты по поглощению такого излучения при лазерном нагреве плазмы, и по ускорению релятивистских электронов в продольном поле. Работы по данной теме опубликованы в ведущих мировых научных журналах и имеют высокий уровень цитируемости. Рекомендация об эффективности лазерной резки металлов радиально-поляризованным лучом нашла подтверждение в экспериментах, проведенных в компании Trumpf, Германия.

Эллипсометрические параметры, характеризующие состояние поляризации в выбранной точке поперечного сечения луча: Отношение длин осей эллипса (a/b); Ориентация эллипса θ в выбранных координатах; Направление вращения вектора поля; Фаза φ в заданный момент времени.

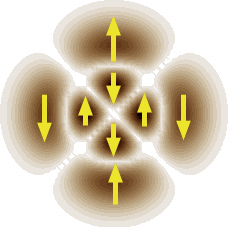
Выходное излучение большинства современных лазеров является поляризационно-однородным. В этом случае эллипсометрические параметры излучения во всех точках поперечного сечения лазерного пучка одинаковы. Распределение амплитуды поля в поперечном сечении луча (поперечные моды) при однородной поляризации описывается решением скалярного волнового уравнения. Для круглых зеркал это Лагерр – Гауссовы моды. Среди решений векторного волнового уравнения есть класс поляризационно-неоднородных мод (ПНМ). В этих модах один или несколько эллипсометрических параметров не являются постоянными по сечению луча. Например, радиально и азимутально поляризованные моды имеют линейную поляризацию в каждой точке, однако, направление поля различно в разных точках поперечного сечения луча. В другом случае от точки к точке изменяется тип поляризации: линейная, эллиптическая, круговая. Наибольший практический интерес представляют моды с радиальным и азимутальным направлением поляризации, имеющие аксиальную симметрию всех параметров лазерного луча, включая поляризацию Некоторые типы поляризационно-неоднородных мод. а – радиально поляризованная, б – угол между вектором поля и радиусом постоянен, в – азимутально поляризованная мода, г – линейная поляризация со сложной топологией вектора поля, д – изменение типа поляризации от точки к точке поперечного сечения луча. Существуют два принципиальных способа получения осесимметрично-поляризованного излучения: Внутрирезонаторный, с использованием, например, дифракционных зеркал с высокой локальной поляризационной селективностью. Специальный рисунок рельефа обеспечивает максимальную добротность резонатора для заданной моды. При этом остальные моды подавляются, имея значительные внутрирезонаторные потери. Этот метод является предпочтительным для мощных лазеров. Внерезонаторные методы формирования ПНМ основаны на когерентной суперпозиции пары обычных мод с помощью интерферометра. Такая техника удобна для лазеров с малой длиной волны, низким коэффициентом усиления и высокой добротностью резонатора. Излучение таких лазеров обладает высоким качеством, имеет высокую пространственную и временную когерентность.

Распределения поля в однородно поляризованных Лагерр – Гауссовых модах TEMpq.

Пример направления поля в моде высокого порядка

Теоретическое описание

Теоретическое описание радиально и азимутально поляризованных мод по этой схеме, с использованием классических решений для Лагерр-Гауссовых мод с однородной поляризацией, нерационально, поскольку классические решения имеют серьезные внутренние противоречия. Представим магнитное поле в виде H=Hφ(r,z)eφ(φ), тогда уравнение ∇H=0 удовлетворяется, а векторное волновое уравнение сводится к скалярному. Его решением в параксиальном приближении является r-z часть известного выражения для Лагерр-Гауссовых мод TEMpq при q=1. Компоненты электрического поля Er и Ez определяются через уравнение Максвелла . Для перетяжки, z=0, решения имеют вид: Здесь R0 = r/w0 ,

Схема образования радиально и азимутально поляризованных мод как суперпозиция «обычных» мод ТЕМ01.

Рассчитанные распределения компонент электрического поля Ez и Er в перетяжке для радиально поляризованных мод различного порядка. Масштабы для Ez и Er взаимно не согласованы.

Учитывая симметрию уравнений Максвелла таким образом можно вычислять компоненты полей для двух классов мод: H=Hφ(r,z)•eφ(φ), E=Er(r,z)•er(φ) + Ez(r,z)ez E=Eφ(r,z)•eφ(φ), H=Hr(r,z)•er(φ) + Hz(r,z)ez Ниже приведены выражения для компонент полей в перетяжке z≈0 для случая острой фокусировки, так называемое приближение Дебая. Здесь θ - угол, определяемый апертурой пучка и фокусным расстоянием линзы f. Аналогичные формулы могут быть записаны и для компонент поля Eφ(r,z), Hr(r,z), Hz(r,z).

Генерация ПНМ с помощью интерферометра Саньяка

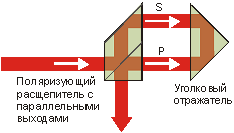
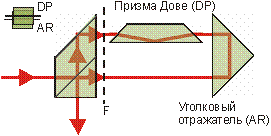
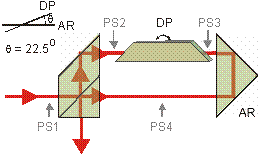
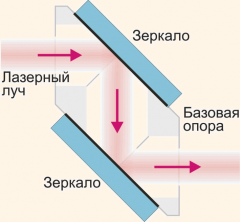
Среди множества схем интерферометр Саньяка выделяется высокой устойчивой к внешним воздействиям на оптическую систему. Причина в том, что оба интерферирующих луча после расщепителя проходят один и тот же путь, двигаясь в противоположных направлениях. Они опять приходят на расщепитель, на котором интерферируют. Поляризующий расщепитель задает правильное направление поляризации лучей. Однако, еще необходимо правильно взаимно сориентировать сами моды, взаимно повернув их на 90°. Делается это путем введения в оптическую схему призмы Дове. Нужный эффект достигается совместным действием призмы и уголкового отражателя.

Схема прохождения лучей по интерферометру Саньяка. 1 – ребро уголкового отражателя; 2 – мода на входе в интерферометр; 3 – лучи сразу после расщепителя; 4 – лучи, интерферирующие на выходе; 5 – мода на выходе из интерферометра.

(a)			Интерферометр Саньяка для генерации радиально и азимутально-поляризованного излучения на оптическом столе
(б)
(в)
	Схема интерферометра Саньяка (a); P и S –поляризации лучей после расщепителя. Схема с призмой Дове (б). Модификация схема интерферометра (в). PS1-PS4 - полуволновые фазосдвигатели.

Экспериментально наблюдаемые моды.

(a)	(б)	(в)
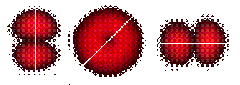
Распределение интенсивности в поперечном сечении лазерного луча (а). Распределение интенсивности за поляризатором-анализатором (б, в). Белая линия – ось поляризатора. Мода с неоднородным по сечению типом поляризацией. (б). Радиально поляризованная мода (в).

Принципиальная схема интерферометрического зеркала для генерации поляризационно-неоднородных мод.

Генерация r- и a-поляризованных мод в мощном CO₂-лазере

Поляризационно-селективные оптические элементы для генерации радиально и азимутально поляризованных мод в мощных СО₂ лазерах.

Дифракционные зеркала для генерации лазерного излучения с осесимметричной поляризацией. а) Фотолитография, химическое травление меди ИПЛИТ РАН 1998 г. б) Алмазное точение, золотое покрытие, компания II-VI США. в) и г) Дифракционное зеркало и аксикон. Алмазное точение. LIMO, Германия.	a	б
	в	г

Схема резонатора технологического СО2-лазера. М1 – выходное зеркало из селенида цинка, радиус кривизны R = 30 м; М2 – M3 – поворотные плоские зеркала; М4 – поляризационно-селективный элемент: дифракционное зеркало, или аксикон

Схема измерения характеристик излучения

Профиль штрихов дифракционного зеркала для генерации азимутально поляризованного лазерного луча.

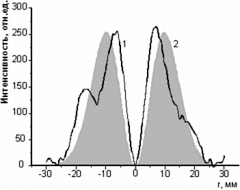
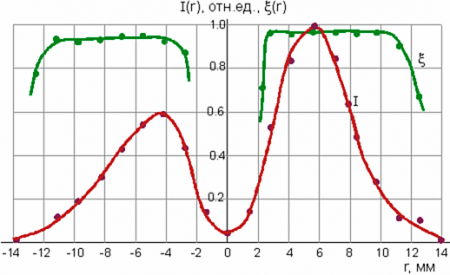
Распределение интенсивности излучения в сечении пучка на расстоянии 16 метров от лазера. Слева – на экране из керамики; справа – экспериментальная 1 и расчетная 2 кривые. Интенсивность излучения I(r)=|E(r)|2.

Радиальное распределение интенсивности I(r) и степени поляризации ξ(r) в ближней зоне. Диаметр диафрагмы 0.9 мм.

Распределение интенсивности азимутально поляризованного излучения в дальней зоне. Слева – ось поляризатора (стрелка) направлена горизонтально; справа - вертикально.

Распределение интенсивности в пучке, отраженном от пластины KCl установленной под углом Брюстера. Интерференция является результатом отражения излучения от двух поверхностей пластины

Распределение интенсивности излучения в дальней зоне. Радиально поляризованная мода TEM_11*
Этот результат, наблюдаемый впервые, получен в трехпроходном резонаторе 4.8 м. Мощность излучения 2 кВт.

Схема преобразования азимутальной поляризации в радиальную с помощью двух полуволновых фазосдвигателей. Угол β=45°.

Преобразование поляризации ПНМ осуществляется с помощью стандартных оптических элементов

Преобразователь азимутальной поляризации в радиальную (или наоборот). Слева - схема устройства одного из трех блоков преобразователя: полуволновой фазосдвигатель. Справа - фотография преобразователя в сборе.

Для мощных СО₂-лазеров в качестве фазосдвигающих пластинок используют только металлические зеркала с соответствующим покрытием.

Спискок публикаций

1. A.V. Nesterov, V.G. Niziev, V.P. Yakunin Generation of high-power radially polarized beam Journal of Physics D Appl. Phys. V.32, (1999), p. 2871-2875.
2. А.А.Гончарский, А.В.Нестеров, В.Г.Низьев, Л.В.Новикова, В.П.Якунин Оптические элементы лазерного резонатора для генерации луча с осесимметричной поляризацией Оптика и спектроскопия, т. 89, вып.1, стр160-164, 2000 г.
3. V.P. Yakunin, A.V. Nesterov, V.G. Niziev. High power CO2 laser with radially polarized beam Proc. .Int. Forum on Advanced High-Power Lasers and Applications, Osaka, Japan, 1999, SPIE v.3889, p. 718-724.
4. A.V. Nesterov, V.G. Niziev. Laser beams with axially symmetric polarization Journal of Physics D Appl. Phys. V.33, (2000), p. 1817-1822.
5. A.V. Nesterov, V.G. Niziev Propagation Features of Beams with Axially Symmetric Polarization J. Opt. B: Quantum and Semiclassical Optics 2001, v.3, n.2, p.215-219.
6. V. G. Niziev, R. S. Chang, A. V. Nesterov Generation of inhomogeneously polarized laser beams by use of a Sagnac interferometer Applied Optics, V. 45, N. 33, p. 8393, 2006.
7. V.G. Niziev, V.P. Yakunin, N.G. Turkin Theoretical and experimental investigation of inhomogeneously polarized laser modes Int. Conf. ICONO/LAT Minsk Belarus 2007. SPIE-6731, 2007.
8. V.G. Niziev, A.V. Nesterov Longitudinal fields in cylinder and spherical modes J. Opt. A: Pure Appl. Opt. 10 (2008) 085005.

В.Г. Низьев