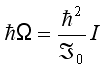Структура ядра как симбиоз кластерной, капельной и оболочечной моделей
Структура ядра как симбиоз кластерной, капельной и оболочечной моделей
Содержание
[убрать]- 1 Основные принципы распределения ядер по группам и квазиоболочкам
- 2 Расположение нуклонов в ядерных квазиоболочках
- 2.1 Группа I
- 2.2 Группа II
- 2.3 Группа III
- 2.4 Группа IV
- 2.5 Группа V
- 2.5.1 Квазиоболочка 6 (Zn70, Ga, Ge70, 72, As, Se76.., Br, Kr)
- 2.5.2 Квазиоболочка 7 (Rb, Sr, Y, Zr, Nb, Mo, Tc, Ru, Rh, Pd, Ag, Cd, In, Sn, Sb)
- 2.5.3 Квазиоболочка 8 (Sb, Te, J, Xe, Cs, Ba, La, Ce, Pr, Nd, Pm, Sm, Eu, Gd, Tb, Dy, Er)
- 2.5.4 Квазиоболочка 9 (Dy, Ho, Er, Tm, Yb, Lu, Hf, Ta, W, Re, Os, Ir, Pt)
- 2.5.5 Квазиоболочка 10 (Pt, Au, Hg, Tl, Pb, Bi, Po, At, Rn, Fr, Ra, Ac, Th, Pa, U, Np, Pu, Am, Cm, Bk, Cf, Es)
- 2.5.6 Квазиоболочка 11 (Cf, Fm, Md, No, Lu, Rf, Db, Sg, Bh, Hs, Mt, 111272 ???)
- 2.5.7 Квазиоболочка 12 (110281???, 112283???, 114289???, 116289???)
- 3 Заключение
- 4 Литература
- 5 См. также
Основные принципы распределения ядер по группам и квазиоболочкам
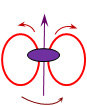
Под структурой ядра подразумевается расположение нуклонов относительно друг друга и главной оси симметрии. Для того чтобы выявить закономерности в расположении нуклонов, необходимо, как минимум, знать характер связи между ними. Предположим, что источником ядерных сил являются две замкнутые глюономагнитные (с нелинейным характером) силовые трубки, которые проходят сквозь нуклон (рис. 1, 2). Их собственный момент равен +1![]() и –1
и –1 ![]() . Предположив, что глюономагнитные трубки отвечают за ядерное взаимодействие, мы можем без выяснения структуры протона заняться определением структуры ядер. В дальнейшем глюономагнитные трубки будем называть ядерными связками (ЯС).
. Предположив, что глюономагнитные трубки отвечают за ядерное взаимодействие, мы можем без выяснения структуры протона заняться определением структуры ядер. В дальнейшем глюономагнитные трубки будем называть ядерными связками (ЯС).
В работе [1] обнаружена аналогия ротационного энергетического спектра сильно деформированных четно–четных (Ч–Ч)ядер с массовым числом А>100 до энергий ε(J) ≈ 4–5 MeV
ε(J) = ВJ(J+1)(1–DJ(J(J+1)+ …) (1)
с джозефсоновскими колебаниями
ε(J) ≈ ε0sin2(π|J|/N). (2)
где Z – заряд ядра, N – подгоночный параметр, π(J(J+1))1/2/Z = π|J|/Z.
Аналогия наблюдается при значении, В ≈ εf (4/3Z)2, D ≈ 2(4/3Z)2, εf = 37 МeV, ε0 = εf(4/3π)2 ≈ 6,664 МeV. Параметр ε0 является общим для всех ядер.
Предположим, что 37 МeV есть энергия возбужденного состояния ЯС (ε*cv), а 31 МeV ее невозбужденное состояние (εcv). Тогда при 2·(ε*cv+ εcv) получим массу π0-мезона, а при 3ε*cv+ εcv массу π±-мезона. Следовательно, можно предположить, что наши ядерные связки есть не что иное, как часть структуры π-мезона входящего в состав нуклона.
Далее предположим, что связь между двумя или несколькими нуклонами происходит через объединения их ЯС. На рис. 3 показано несколько таких примеров объединения нуклонов. У ядер 2Н, 4Не и 7Li ЯС расположены в одной плоскости.
При дальнейшем увеличении числа нуклонов из них формируется объемный каркас. При формировании из ЯС различных структур должны соблюдаться три ограничения.
- 1. Через нуклон может проходить только две ядерные связки.
- 2. Ядерные связки должны проходить через нуклон сонаправленно.
- 3. Максимальное количество нуклонов связанных одной ЯС не больше восьми.
•Из первого ограничения следует, что объемные структуры могут формироваться только на базе двухмерных поверхностей.
•Из второго следует, что число сторон обязательно должно быть четным. При нечетном числе сторон нарушается принцип сонаправленности прохождения через нуклон.
•Ограничение на количество нуклонов в одной ЯС означает, что ЯС обладает свойством насыщения. Степень насыщения зависит от места расположения связки в ядерном каркасе, симметрии каркаса и от особенности расположения нуклонов в ядре.
- Группу нуклонов с одинаковой направленностью спина и общей ядерной связкой назовем кластером. Нуклон, имеющий общую ядерную связку с группой нуклонов, но отличающийся направлением спина, рассматривается как самостоятельный кластер.
При формировании кластера необходимо учитывать принцип Паули: исключать ситуацию, когда два протона или нейтрона размещаются в одном кластере рядом (сонаправленно). Допускается только чередование протона с нейтроном.
Рассмотренные выше ограничения и принцип Паули определяют алгоритм расположения нуклонов и ЯС в ядре.
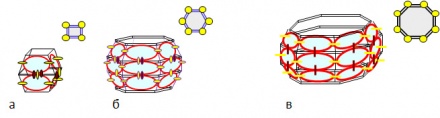
На первом этапе формирования объемной структуры проекция ядерного каркаса вдоль главной оси симметрии имеет квадратную форму (рис. 4а). Начиная с ядра 60Ni, она приобретает форму шестиугольника (рис. 4б), у 70Zn и последующих ядер – восьмиугольника (рис. 4в).
Симметрия относительно главной оси ядра является определяющим фактором при распределении ядер по группам. Внутри группы структура ядерного каркаса отличается числом ярусов. Количество ярусов определяем по числу рядов из ЯС, в которых имеются узловые точки с вертикальной ориентацией момента нуклона.
- Совокупность ядер с одинаковой симметрией ядерного каркаса и одинаковым количеством ярусов назовем квазиоболочкой .
В предложенной закономерности размещения ядер по группам и квазиоболочкам есть исключение. Ядра первой и второй квазиоболочки обладают одинаковой симметрией каркаса и одинаковым количеством ярусов из ЯС, но у них разная структура нуклонных узлов. В вертикальных узлах первой квазиоболочки размещаются и протоны, и нейтроны. Их количество может изменяться. В вертикальных узлах второй и последующих квазиоболочек размещаются только нейтроны. Их число в пределах одной квазиоболочки фиксировано. Такое изменение в вертикальных узлах секторов приводит к существенным различиям в свойствах ядер в целом, что и оправдывает их размещение в разные группы.
Все ядра с шестиугольной и восьмиугольной симметрией каркаса в центре имеют кластер из четно-четных (Ч-Ч) ядер (рис.39). Самый легкий кластер – 12С в ядре 60Сo. Самый тяжелый – 90Zr в ядре 116289???. Обнаружена взаимосвязь между деформацией внутреннего кластера и деформацией ядра. Чем больше размер внешнего кластера ( Kl .) тем он эластичней. Когда в его центре размещается кластер, его деформация отражается на деформации внешнего кластера, т.е. поверхности ядра. Это является определяющим фактором в определении параметров внутреннего кластера для Ч-Ч ядер. Для Н-Ч и Н-Н ядер приоритетно значение его спина и магнитного момента.
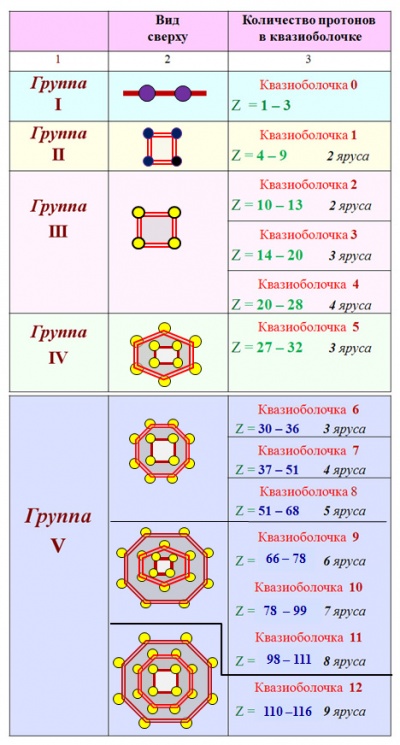
В таб. 1 показано, как размещаются ядра по группам и квазиоболочкам.
При размещении ядер по квазиоболочкам ориентируемся на стабильные ядра или, если те отсутствуют, на долгоживущие изотопы. Во втором столбце показаны проекции квазиоболочек вместе с нуклонами в вертикальных узлах. Белый круг обозначает нейтрон. Внутри проекций каркасов ядер четвертой и пятой группы показаны проекции внутренних кластеров.
Сформулируем основные правила определения спина ядра (J), его орбитального (l) и магнитного момента (μ), суммарного момента нуклонов (J) и момента ядерной связки (lcv).
- Правило 1. Определение спина нуклонов в кластере.
- Спины нуклонов, находящихся в одном кластере, суммируются.
- Спины нуклонов, находящихся в одной ядерной связке, но с противоположной направленностью спинов, компенсируются.
- Правило 2. Определение результирующего спина кластеров
- Если кластеры пронумеровать, то спин и магнитный момент четных кластеров компенсирует спин и магнитный момент нечетных кластеров.
- Правило 3. Определение орбитального момента ядра.
- Орбитальный момент численно равен количеству сгенерировавших его нескомпенсированных нуклонов. Орбитальный момент ядра есть не что иное, как спин ядерного каркаса.
- Правило 4. Определение спина ядра.
- Сумма результирующего спина нуклонов, орбитального момента ядра и момента ядерной связки есть экспериментальный спин ядра.
- Спин ЯС появляется в трех случаях:
- – нечетный нуклон расположен в периферийной ЯС;
- – ядре четное количество ЯС, но одной из них момент равен не 1, а 2;
- – в ядре нечетное количество ЯС, но у одной из них спин равен 1, а у остальных 2.
- Правило 5. Определение магнитного момента кластера и ядра.
- Магнитные моменты нуклонов, находящихся в одном кластере, определяются так же, как и спины нуклонов, но с учетом знака (протон "+", нейтрон "–").
- Экспериментальный магнитный момент ядра есть результат суммирования (вычитания) магнитного момента нескомпенсированных нуклонов и орбитального магнитного момента ядра.
Если при определении спина ядра орбитальный момент суммируется с результирующим спином нуклонов, то и орбитальный магнитный момент суммируется с магнитным моментом нуклонов. Если орбитальный момент вычитается, то и магнитный момент вычитается.
Введение поправочного коэффициента k, позволяет учитывать изменения магнитного (зарядового) радиуса протона и нейтрона в связанном состоянии, по отношению к их свободному состоянию.
- Если нуклоны из одной ядерной связки находятся в одном кластере, производится деление на коэффициент k, если в разных кластерах – умножение.
Спин ядра, имеющего объемную структуру, определяется по такой же методике, как и у легких ядер, только вместо кластеров каркаса рассматриваются вертикальные сектора (их число равно числу сторон ядерного каркаса). Внутри сектора определяется результирующий спин нуклонных кластеров с использованием правила 2. Результирующий спин всех секторов определяет спин ядерного каркаса (орбитальный момент ядра) с применением правила 3. Например, при спине 3/2 орбитальный момент ядра равен трем, а при спине 1 – двум. В перечисленных выше случаях к орбитальному моменту ядра может еще добавляться (вычитаться) момент ЯС. Определение спина ядра сведено в таб. 2.
Формально ЯС можно рассматривать как некие рамки (с собственным моментом), а нуклоны – как вращающиеся гироскопы, через ось которых проходит рамка. Как ни парадоксально, классический подход при определении экспериментального спина и магнитного момента позволяет найти взаимосвязь между четырьмя параметрами ядра: экспериментальным спином, магнитным моментом, результирующим спином нуклонов и орбитальным моментом ядра.
- Размещая нуклоны так, чтобы согласовать все эти параметры, мы тем самым определяем расположение нуклонов относительно друг друга и главной оси симметрии.
В предлагаемой структуре у всех ядер с объемной конфигурацией обязательно имеются нуклоны с ортогональным моментом относительно момента других нуклонов. Как уже отмечалось, при наличии несбалансированных нуклонов (или нечетного нуклона), каркас приобретает момент импульса. Из-за ортогонального расположения момента нечетного нуклона по отношению к оси симметрии каркаса, каркас (ротатор) стремится вращаться в ортогональной плоскости по отношению к его оси симметрии. При ортогональном вращении возникает гироскопический момент, который приводит к прецессионным колебаниям нуклонов. Прецессионные колебания вызывают вибрационные колебания каркаса. Следовательно, ротационный спектр необходимо рассматривать в едином комплексе с вибрационным (фононным) спектром
Н = Нrot + Hνib+ Hνib -rot. (3)
В модели самосогласованных фононов (3) [2], рассматривающей в едином комплексе ротационный и вибрационный спектр, получено хорошее качественное соответствие расчетов квадрупольно-октупольных спектров ядер редкоземельной области с экспериментом. Параметрами этой модели служат коллективная масса Сr, жесткость Вr (или![]() Ω) и статический момент инерции ядра.
Ω) и статический момент инерции ядра.
При достижении критического значения момента появляется backbending ядра. Так как жесткость каркаса не беспредельна, то он деформируется. Деформация сопровождается падением под твердотельную линию:
– твердотельное значение момента инерции ядра.
В [3] отмечается высокая предсказуемость соотношения
Е(I) = a1I + a2I2 + a3I3, (6)
где параметры а1, а2, а3 определяются моментом инерции основного состояния, параметром мягкости и параметром асимметрии ядра. В нашей интерпретации хорошее совпадение этой модели с экспериментом связано с тем, что учтено изменение жесткости каркаса и асимметрии, которую вносит нечетный нуклон.
Также с экспериментальными данными совпадает гамильтониан Н-Н ядра в модели «аксиальный ротатор +2 квазичастицы»
Н = Нn + Hp + А [I2 – I2z - 2 [I+J- + I-J+] + (J2 – J2z )] + Vnр, (7)
где А – инерционный параметр, Hn, Hp – одночастичные гамильтонианы нейтрона и протона, J = jn + jp, член [I+J– + I–J+] – кориолисовое взаимодействие нечетных нуклонов с вращением остова I± = IХ ± iIY, J± = JХ ± iJY, индексы х и у – проекции на оси, перпендикулярные оси симметрии z [4]. Член в круглых скобках представляет собой энергию отдачи ротатора, которая зависит только от квантовых чисел нечетных нуклонов. В гамильтониане (7) учитываются основные факторы, влияющие на природу энергетического спектра; они согласуются с предложенной структурой ядра. Покажем это на примере анализа структуры некоторых ядер. В работе [5] рассмотрена структура значительно большего количества ядер, подробно –структура ядер четырех радиоактивных рядов. В настоящей статье структура некоторых ядер, предложенная в [5], пересмотрена.
Расположение нуклонов в ядерных квазиоболочках
Группа I
Квазиоболочка 0 (Н, Не, Li)
В квазиоболочку вошли легкие ядра, не имеющие объемной структуры. Начинается ядром водорода и заканчивается ядром 7Li (рассматриваются только стабильные ядра).
2Н(1) (рис. 5). Протон и нейтрон с одинаковым направлением спина располагаются сонаправленно. На рис. 5б показан упрощенный вариант: ЯС изображена в виде прямоугольника. Под рисунком приводится методика определения спина ядра и его магнитного момента. Суммарный спин нуклонов равен 1. Следовательно, орбитальный момент ядра равен 2. Вычитая из J момент каркаса (орбитальный момент ядра), получаем спин ядра (J – l = J).
Магнитный момент данного ядра есть сумма магнитных моментов входящих в него протона и нейтрона (с учетом знаков р и n). Орбитальный момент при определении магнитного момента в данной конфигурации не участвует, т.к. протон находится на оси вращения ядра. Увеличение радиуса шубы при слиянии двух нуклонов экспериментально отражается на изменении их магнитного момента. Магнитный момент дейтерия равен 0,8574μ (значения взяты из [6], [7]), т.е. в 1,026 раз меньше суммарного момента протона и нейтрона в свободном состоянии. Уменьшение магнитного момента дейтерия связано с непропорциональным увеличением шубы протона и нейтрона. Радиус шубы нейтрона увеличивается больше, чем зарядовый радиус шубы протона.
3Н(1/2) (рис. 6). Базовой для этого ядра является структура 2Н. Дополнительный нейтрон расположен так, чтобы компенсировать магнитный момент и спин первого нейтрона. Несбалансированный протон генерирует вращение ядерного каркаса, но т. к. число ЯС нечетно, необходимо учитывать момент ЯС, который приводит к компенсации орбитального момента ядра (J = J ± l* = 1/2 ± 0 = 1/2, где l* = l – lсv = 1 – 1). Знак плюс или минус пред результирующим орбитальным моментом (l*), определяется из экспериментального значения магнитного момента.
3Не(1/2) имеет структуру 3Н с зеркальной заменой протонов на нейтроны. Структуры 3Н и 3Не позволяют определить, как изменяется магнитный момент протона и нейтрона. В ядре трития зарядовый радиус протона увеличивается в 1,0666 раза (2,97896/2,7928). В ядре 3Не радиус нейтрона увеличивается в 1,112 раза (2,1276/1,913). Таким образом, зарядовый радиус нейтрона больше зарядового радиуса протона в 1,0427 раза. Деформационный коэффициент нуклона в ядрах 3Н и 3Не больше, чем в ядре 2Н, т. к. он зависит от количества нуклонов в ЯС.
4Не(0) (рис. 7). Ядро состоит из двух дейтонных кластеров и трех ЯС. Протон размещается на одной линии с протоном, нейтрон напротив нейтрона. Спины и магнитные моменты дейтронов скомпенсированы. Нулевой баланс момента ЯС восстановится, если положить момент центральной ЯС равным 2. Экспериментальные значения зарядовых радиусов 4Не, 3Не и 3Н равны соответственно Rch = 1,674 фм, Rch = 1,967 фм, Rch = 1,76 фм [8]. Деформация (β) ядра 4Не равна +0,172 (вытянуто) [9].
5Не(3/2) (рис. 8). Добавив в периферию ядра 4Не нейтрон, мы получим структуру 5Не.
6Не(0) (рис. 9). Добавляется еще один нейтрон. Спин ядра нулевой при нечетном числе ЯС. Следовательно, три центральные ЯС имеют двукратное возбуждение, четность которых (т.е. знак поляризации) (+, +) или (–, –). Если четность первой ЯС (+), то у следующих за ней (– –), (+ +), (– –) и (+). Результирующая четность ЯС равна нулю. Средний квадратичный радиус 6Не 2.48фм [10]. При энергии 0.98 MeV 6Не распадается на α-кластер и два нейтрона.
8Be(0) (рис. 10). В ядре 8Ве имеются два уровня с энергиями возбуждения 16,62 МeV и 16,92 МeV [11]. Эти уровни имеют одинаковое квантовое число Jπ = 2+ и разный изоспин. Физический смысл изоспина в 8Be связан с процессом перезарядки нуклонов в центральном кластере. Перезарядка сопровождается вибрационными колебаниями вдоль оси кластера, что связано с принципом Паули. Высокий уровень возбуждения (Е*(2+) ~ 16,62 МeV и 16,92 MeV) означает, что в формировании ядра участвуют ЯС с моментом lcv = 2. Радиус ядра 8Be равен 2,5 фм [12]. В αα-системе существует узкий брейт-вигнеровский резонанс 8Ве(0+) [13] с энергией Еr = 92,12 ± 0,05 keV, Г = 6,8 ± 1,7 eV. Возможно, природа резонанса связана с колебаниями двух периферийных дейтронов относительно центрального кластера.
Если удалить в 8Be один периферийный кластер (т.е. 2H), получим 6Li. Удалив один протон из центрального кластера 8Be, получим ядро 7Li.
Группа II
Квазиоболочка 1 (Be, B, C, N, O)
В первую квазиоболочку вошли ядра, имеющие объемную конфигурацию из двух ярусов ЯС (рис.11). В проекции вдоль главной оси ядра это квадрат (рис. 12в). При формировании объемной структуры из ЯС необходимо учитывать, что они в противоположном секторе каркаса имеют противоположную четность. Следовательно, и моменты нуклонов в этих узлах меняют поляризацию. Ядерные связки каркаса развернутые в плоскость дают следующее сочетание четности +, –, +, – (рис. 12а). Свернув ЯС в квадрат, получим +, +, –, – (рис. 12б, в). При этом сонаправленость ЯС в нуклоне сохраняется. Особенность этой квазиоболочки состоит в том, что в горизонтальном ярусе находятся только нейтроны, их число фиксировано. Следовательно, нейтроны с противоположно направленными моментами взаимно скомпенсированы и не участвуют в определении момента каркаса. Спин каркаса определяется нечетным нуклоном в узле вертикального сектора по той же методике, что и раньше.
На (рис. 13) показана структура ядра 9Ве(3/2). Это первое стабильное ядро с объемной структурой. Результирующий момент нуклонов равен –1/2. Следовательно, l = 1. Добавив орбитальный магнитный момент ядра к моменту нейтрона, получим μ = 0,913. Экспериментальное значение магнитного момента равно –1,18, следовательно, нейтрон увеличивает свой радиус в 1,14 раз.
Структура 12С показана на (рис 14). Из рисунка видно, что в первом ярусе имеется две нейтронные, а во втором ярусе – две протонные вакансии. При их заполнении получим магическое ядро 16О (рис. 17). Если предположить, что ЯС в первом ярусе находятся в возбужденном состоянии (lсv = 2), то нулевой спин первого возбужденного уровня 16О есть следствие возбуждения ЯС второго яруса каркаса. Структура ядра 16О уже позволяет понять природу распределения нуклонов по оболочкам в оболочечной модели. Это связано с симметрией каркаса из ЯС, с симметрией расположения в нем нуклонов, со свойством насыщения ЯС и принципом Паули.
Переход от ядра 13С к ядру 13N (рис. 15, 16) связан не только с превращением нейтрона в протон, но и с переходом нечетного нуклона в другой ярус. На (рис. 18, 19 и 20) показана структура ядер 17О, 17F и их энергетический спектр возбуждения. Необычное значение магнитного момента 17О означает, что у ядра большой орбитальный момент, что возможно за счет трех несбалансированных нуклонов.
Группа III
Квазиоболочка 2 (O, F, Ne, Na, Mg, Al, Si)
Базовая структура квазиоболочки дана на рис. 21. Начиная со второй квазиоболочки, в узлах вертикальных секторов размещаются только нейтроны (обозначены штриховым контуром) (рис. 22). Результирующий магнитный момент и спин узловых нейтронов вертикальных секторов всегда равен нулю. Для удобства восприятия рисунка мы эти нейтроны не изображаем, а пишем (слева от рисунка) их количество. Мелким курсивом число нейтронов в горизонтальных узловых точках каркаса. Как и впервой квазиоболочке необходимо учитывать изменение четности при формировании из ЯС объемной структуры. Для простоты определения, четность нижнего нуклонного яруса разделим на две части. В левой части все нуклоны имеют положительную четность, а в правой части – отрицательную. Если нуклон в процессе ядерной реакции переходит из своего яруса на соседний, его четность меняется.
18O(0) (рис. 22). Это первое стабильное ядро, имеющее объемный каркас, где в вертикальных узлах только нейтроны. Ядерный каркас построен из двух ярусов ЯС с вертикальными узлами и одного "пустого" яруса (без вертикальных узловых нейтронов.) На рис. 23 – 25 показана структура 19Fe, 19Ni и их энергетический спектр возбуждения. Схожесть энергетического спектра позволяет сделать предположение о схожести в возбужденном состоянии их каркаса.
При возбуждении 19Fe протон из экватора перемещается в верхний ярус, образуя ЯС. Количество ЯС в обоих ядрах становится равным. При возбуждении еще одной ЯС в обоих ядрах получим спин 5/2+. То, что энергия возбуждения 19Ni выше энергии возбуждения 19Fe, означает, что каркас 19Ni является более жестким, чем каркас 19Fe.
Квазиоболочка завершается ядром 28Si (рис. 28). Ядро имеет аномально большую сплющенную форму (β = –0,360). Природа такой деформации связана с размещением двух "лишних" протонов в экваторе каркаса. При удалении двух протонов и двух нейтронов (рис. 27, 24Mg) получим симметричное расположение нуклонов. Но, тем не менее, 24Mg не относится к категории дважды магических ядер. Это связано с его аномально большой вытянутой деформацией (+0,610). Аномальная деформация сохраняется и у 20Na (+0,350), где два протона удалены из верхнего яруса (рис. 26). При размещении 20Na, 24Mg и 28Si в центре более массивных кластеров, их аномально большие деформации отражаются на деформации всего ядра.
•Аномальные перепады деформации можно использовать в качестве ориентира для определения структуры более массивных ядер. Например, берем каркас, в котором 42р и 66n, и размещаем в нем 24Mg (+0,610) и получаем ядро 132Хе26,9% с +0,116. Если в центре того же каркаса разместить 28Si (–0,360), получится ядро 136Ba7,85% с β = –0,159.
Квазиоболочка 3 (Si, P, S, Cl, Ar, K, Ca)
Квазиоболочка формируется из трех ярусов ядерных связок (Рис. 29). Слева от рисунка двенадцать нейтронов вместо восьми. Магические числа третьей квазиоболочки – 16n и 20n, 16р и 20р. При Z = 16 деформация ядра аномально большая, поэтому это число не входит в категорию общепринятых магических.
29Si(1/2) (рис. 30). Это первый стабильный изотоп с тремя ярусами. Все три "лишних" нейтрона размещены в экваторе каркаса. На первом этапе эволюции ядра с ростом числа нуклонов происходит формирование экваториальной области каркаса из двух нуклонных ярусов. Это хорошо видно на примере структуры 32S (рис. 31). При дальнейшем росте числа нуклонов они размещаются в полюсе каркаса (рис. 32, 33).
Ядро 40Са замыкает третью квазиоболочку. Оно дважды магическое и имеет почти сферическую форму. Если предположить, что второй и третий ярус ЯС находятся в возбужденном состоянии, то первое возбужденное состояние 40Са (J*= 0) связано с возбуждением первого яруса. Наличие двух "пустых" периферийных ЯС свидетельствует о насыщении квазиоболочки нуклонами.
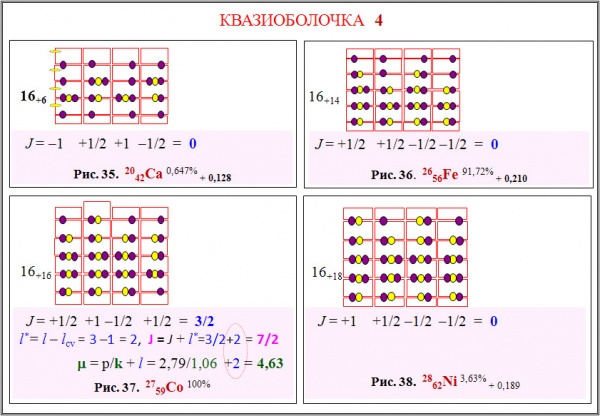
Квазиоболочка 4 (Ca, Sc, Ti, V, Cr, Mn, Fe, Co, Ni)
Четвертая квазиоболочка является четырехъярусной (рис. 34). Она начинается ядром 42Са(0) (рис. 35) и завершается ядром 62Ni (рис. 38). Из рисунка видно, что ядро 62Ni имеет грушевидную форму. Его деформация чуть меньше чем у 56Fe, т.к. в экваториальной области нуклонные вакансии закрыты. Все ядра квазиоболочки имеют вытянутую форму. Большая деформация 56Fe (рис. 36) (+0,210), большое значение спина у 59Со(7/2) (рис. 37) и наличие в каркасе двух "пустых" ярусов из ЯС свидетельствуют о насыщении этой квазиоболочки нуклонами.Ядро 60Ni имеет неожиданно сплющенную деформацию (–0,178). Следовательно, 62Ni (+0,189) остался в четвертой квазиоболочке, а 60Ni перешел в следующую, претерпев значительные качественные изменения структуры ядерного каркаса.
Группа IV
Квазиоболочка 5 (Co, Ni, Cu, Zn, Ge, Se)
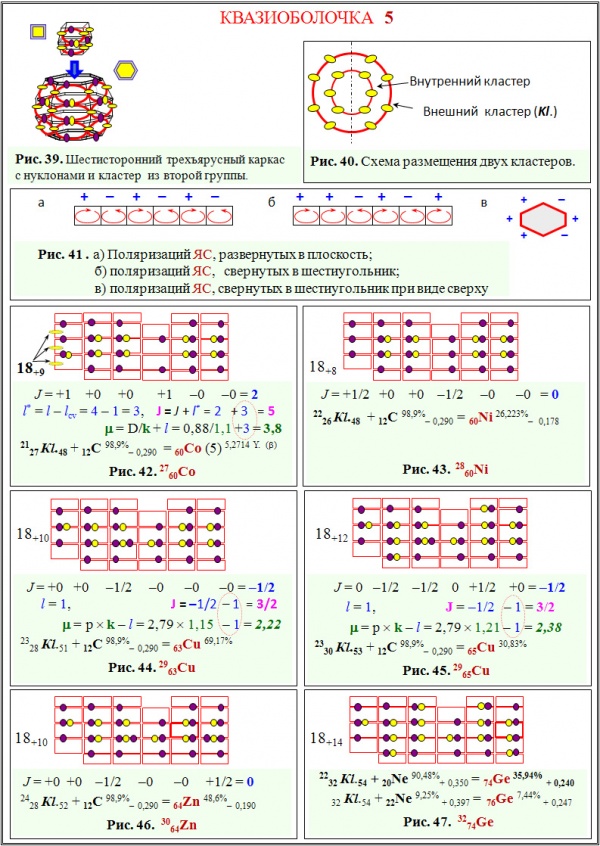
Каркас пятой квазиоболочки (рис. 39) имеет шестиугольную форму и состоит из трех ярусов ЯС. Если в предыдущем каркасе было 24 ЯС, то в этом их 28. Возвращение 62Ni в четвертую квазиоболочку связано с особенностью шестиугольной конфигурации. На рис. 41 а изображена четность ЯС в плоскости. Сворачивание каркаса в шестиугольник меняет четность ЯС. На рис. 41 б изображена четность ЯС, свернутых в шестиугольник. На рис. 41 в – проекция вдоль главной оси симметрии каркаса.
Из рис. 41 в видно, что в шестиугольнике противоположная сторона не может иметь другую четность. Поэтому необходимо рассматривать компромиссный вариант, где два противоположных сектора с одинаковой четностью (назовем их "ослабленными") имеют меньшее количество нуклонов и ЯС. У одного из "ослабленных" секторов нуклон смещен на один ярус, что меняет его четность.
Как мы уже отмечали, все ядра с числом секторов шесть и выше имеют внутри каркаса кластер (рис. 39 и 40). Так как шестиугольная конфигурация оболочки более эластична, чем четырехугольная, то деформация внутреннего кластера отражается на деформации внешнего кластера, а значит и на деформацию ядра.
60Со(5) (рис. 42) имеет шестиугольную конфигурацию из трех ярусов ядерных связок. В верхнем и нижнем нуклонном ярусах имеется по одной нуклонной вакансии. Внутренний кластер – 12С (т.к. это первое Ч–Ч ядро с объемным каркасом), придает внешнему кластеру дополнительную жесткость, что подавляет многомодовость гигантского резонанса. Теперь параметры "дыхательной" моды зависят не только от параметров внешнего кластера, но и от параметров внутреннего. Причина большого спина ядра связана с особенностью структуры каркаса (точнее с четностью ядерных связок в его секторах). Количество нечетных нуклонов равно 4. Следовательно, l = 4. Вычитая из орбитального момента, момент ядерной связки, получим l* = 3.
60Ni (рис. 43). Изменение четности протона, которым сопровождается его "уход" на другой ярус, уменьшает конфликтную связь первого и четвертого секторов каркаса. На рис. 44, 45 показана структура ядер 63Cu и 65Cu. Зная, что у этих ядер одинаковый спин, но разный магнитный момент, можно определить степень влияния дополнительных нейтронов на зарядовый радиус протона. Структура ядра 64Zn каких–либо "сюрпризов" не имеет (рис. 46), а в ядрах 74Ge и 76Ge (рис. 47) появилась одна особенность. Большая деформация ядер Ge свидетельствует о том, что у внутренних кластеров она аномально большая. Следовательно, в качестве внутреннего кластера выступает 10Ne, как первое ядро с большой вытянутой деформацией (β = +0,350).
Группа V
Квазиоболочка 6 (Zn70, Ga, Ge70, 72, As, Se76.., Br, Kr)
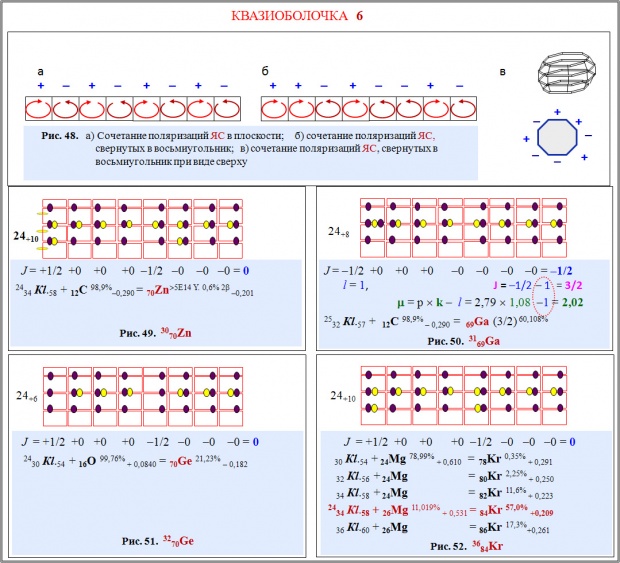
Каркас ядер пятой группы имеет восьмиугольную структуру. Самые первые ядра формируются на базе трех ярусов ЯС (24 ЯС) и еще одного "пустого" яруса (без узловых нейтронов). С ростом числа нуклонов происходит увеличение числа ярусов. Последнее стабильное ядро находится в десятой квазиоболочке и имеет семь ярусов. В отличие от четвертой группы, в пятой каких-либо проблем с четностью ядерных секторов не возникает: сектор на противоположной стороне каркаса имеет другую четность (рис. 48 б, в).
У всех ядер этой группы в центре имеется кластер (min ~ 12С, max ~ 90Zr). Т.к. у ядер массивнее 62Ni имеется собственный кластер, то ядра массивнее полония имеют в своей структуре уже по два внутренних кластера. Так же, как у ядер четвертой группы, деформация внутреннего кластера отражается на деформации ядра.
Известно, что массивные ядра, как правило, имеют вытянутую форму. Это связано с двумя факторами: а) вытянута форма четвертой квазиоболочки; б) у тяжелых ядер во внешнем каркасе большое число ярусов из ЯС.
Почти сферическая форма изотопов ртути связана с тем, что их кластером является 60Ni. Его сплющенная деформация накладывается на вытянутую деформацию внешнего каркаса и, следовательно, результирующая деформация ядра минимальна.
70Zn (рис. 49). Изотоп 70Zn открывает самую большую ядерную группу. Внутренним кластером ядра 70Zn является 12С. У 70Zn деформация равна –0,201. У следующего ядра (70Ge) β = –0,182. Уменьшение деформации связано с размещением внутри каркаса 16О (β = +0,0840). Почти сферическая форма ядра кислорода незначительно сглаживает сплющенную форму. Правила определения спина и магнитного момента у ядер с восьмиугольной конфигурацией сохраняются. В качестве примера приводим 69Ga(3/2) (рис. 50). У ядер 70Ge и 78Kr одинаковый внешний кластер, но разные внутренние кластеры (рис. 51 и 52). На рис. 52 изображен самый распространенный изотоп криптона. Под рисунком приведены параметры еще шести изотопов. Большое количество стабильных изотопов связано с магическим числом протонов (24р). Аномально большая деформация 24Mg (+0,610) отражается и на деформации изотопов Kr. С ростом распространенности деформация изотопа уменьшается. У самого распространенного изотопа она наименьшая (+0,209). Возможно, что деформацию уменьшает замена 24Mg на 26Mg (β = +0,531). Дальнейшее увеличение нейтронов в каркасе ядра Kr приводит к росту деформации ядра.
Квазиоболочка 7 (Rb, Sr, Y, Zr, Nb, Mo, Tc, Ru, Rh, Pd, Ag, Cd, In, Sn, Sb)
На рис. 53 – 56 показана структура ядер 85Rb, 98Mo, 102Ru и 120Sn. На примере ядер 102Ru и 120Sn хорошо видно влияние внутреннего кластера на их деформацию. Например, у изотопов молибдена сферическая форма связана с деформацией 16О (β = +0,0840). Вытянутая форма у Ru, с деформацией 20Ne (+0,0350) и сплющенная форма изотопов олова с 30Si (–0,321).
Большое количество стабильных изотопов означает, что у ядерных каркасов этой квазиоболочки высокая прочность. У нечетных ядер рост массы внутреннего кластера немного отстает от роста массы внутреннего кластера Ч–Ч ядер, что приводит к непропорциональному росту их зарядового радиуса. В следующей квазиоболочке ситуация с непропорциональным ростом зарядового радиуса для Н–Ч ядер повторяется.
В [14] отмечается загадочность совпадения спектров ядер 114Sn и 118Xe. Их внешние кластеры имеют по два "дефектных" сектора (рис. 57, 58). И хотя у ядер разные внутренние кластеры (Si и Mg) и разная деформация, спектральное совпадение обусловлено этими секторами.
Квазиоболочка 8 (Sb, Te, J, Xe, Cs, Ba, La, Ce, Pr, Nd, Pm, Sm, Eu, Gd, Tb, Dy, Er)
С возрастанием числа ярусов ЯС увеличивается масса кластеров в центре квазиоболочки. Если в предыдущей квазиоболочке самым легким кластером был 12С, то здесь таковым стал 16О. Самый массивный кластер состоит из 54Cr2,365% (β = +0,230). На рис. 59 – 60 изображена структура первого (123Sb) и последнего (164Er). Аномально большое значение спина (7/2) у 123Sb, как видно из рис. 59, связано с необычным расположением ЯС. В шестом секторе ядерного каркаса пять ЯС и плюс "пустая" ячейка. Момент "пустой ячейки (lemp) равен моменту ЯС из второго сектора, но с противоположным знакомэ. Суммарный спин пяти ЯС равен 1 (2 – 2 + 2 – 2 + 1 = 1). Следовательно, lcv = lemp + l5cv = 2 и как результат J = J + l + lcv = J + l* = 1/2 + 3 = 7/2,μ = (2n – p)×k + l* = (3,82 – 2,79)×1,06 + 3 = 3,36.
В качестве наглядного примера влияния деформации внутреннего кластера, на деформацию ядра, приведена структура ядер 130Те и 138Ва. При размещении в центре массивного кластера, состоящего из 42р и 68n, ядра 20Ne (β = +0,350) получим 130Те с β = +0,120. Все изотопы этого ядра также с вытянутой деформацией. Если в этом же массивном кластере разместить 28Si (β = –0,360) получим 138Ва с β = –0,120. Сплющенная деформация наблюдается и у изотопов.
Квазиоболочка 9 (Dy, Ho, Er, Tm, Yb, Lu, Hf, Ta, W, Re, Os, Ir, Pt)
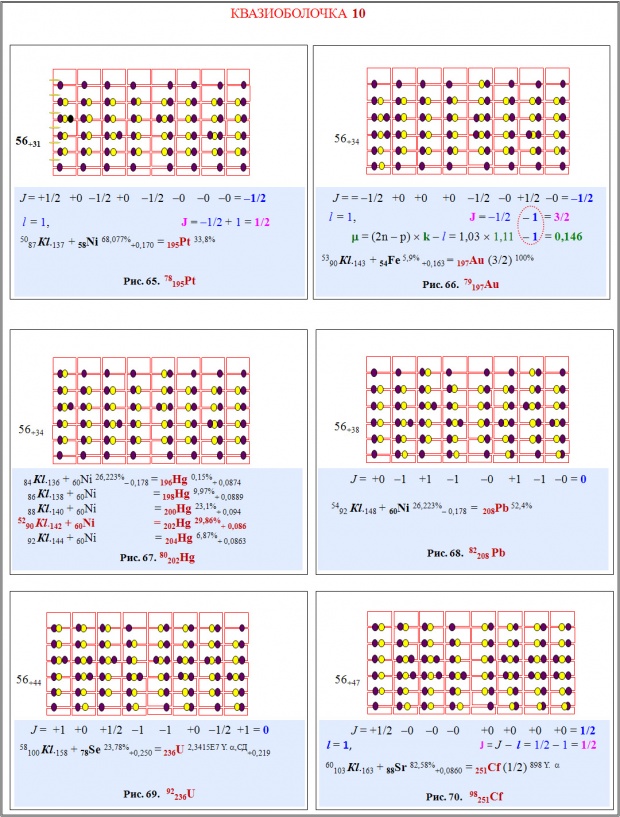
На рис. 63 и 64 изображено структура первого (164Dy) и последнего (194Pt) ядра этой квазиоболочки. Нуклоны в 164Dy относительно экватора имеют полностью симметричное расположение. В ядре 194Pt симметрия расположения нуклонов относительно экватора нарушена. В качестве внутреннего кластера является 62Ni, т.е. самое массивное ядро из четвертой квазиоболочки.Квазиоболочка 10 (Pt, Au, Hg, Tl, Pb, Bi, Po, At, Rn, Fr, Ra, Ac, Th, Pa, U, Np, Pu, Am, Cm, Bk, Cf, Es)
Это последняя квазиоболочка, содержащая стабильные ядра. Ее особенность в том, что в центре размещены кластеры не только из третьей группы (квадратный каркас), но и ядра с шестиугольным и восьмиугольным каркасом. Например, в центре 236U (рис. 69) – ядро 78Se, которое принадлежит шестой квазиоболочке, т.е. имеет восьмиугольный каркас из трех ярусов. В экваторе 78Se расположено 16 нуклонов, в экваторе внешнего кластера 236U – 24 нуклона. В процессе радиоактивного распада 236U внутренний кластер превращается в 60Ni (рис. 68). Если внешний каркас 236U имел 158 нуклонов, то после цепочки радиоактивных распадов остается 148. Используя экспериментальные значения спина, магнитного момента, (у Ч–Ч данные о деформации) можно определить, какие нуклоны участвуют на каждом этапе распада ядра 236U.
Изотоп 194Pt завершает девятую квазиоболочку, а 195Pt открывает десятую квазиоболочку. Распространенность изотопов соответственно равна 33,8% и 32,9%. Если экватор внешнего кластера определять относительно вертикальных узловых нейтронов, то два протона и нейтрон относительно его смещены вниз. Следовательно, внешний кластер имеет грушевидную форму. Экспериментально грушевидная форма может и не проявляться, т.к. смещение внутреннего кластера в верхнюю часть экватора ядра снижает этот эффект. У 197Au (рис. 66) грушевидная форма поверхности внешнего кластера усиливается, экспериментально это должно отражаться на поведении энергетического спектра. Аномально малое значение магнитного момента 197Au связано с особенностью расположения двух нейтронов. Магнитный момент нейтрона, находящегося в первом секторе последнего нуклонного яруса, суммируется с магнитным моментом нейтрона из пятого сектора первого яруса. Вычитая из этой суммы магнитный момент нечетного протона, с учетом поправочного коэффициента и вычитая орбитальный магнитный момент, получим μ = 0,146.В ядре 208Pb, как и в 202Hg в качестве внутреннего кластера является 60Ni (квазиоболочка 6). Данные о деформации 208Pb в [9] отсутствуют. Из рис. 68 видно, что деформация должна быть сопоставима с деформацией ядра 202Hg, но с усиленной грушевидной формой ядра.
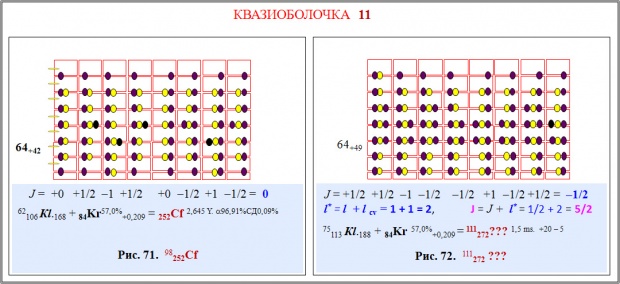
Квазиоболочка 11 (Cf, Fm, Md, No, Lu, Rf, Db, Sg, Bh, Hs, Mt, 111272 ???)
Все разнообразие параметров внутреннего кластера у 100255Fm – 108265Hs ограничено изотопами криптона.
252Cf(1/2) (рис. 71). Внутренним кластером является 84Kr. По протонам в каркасе имеется две вакансии. Два "лишних" нейтрона заняли нижний ярус.111272???(5/2) (рис. 72). Размещая в качестве внутреннего кластера 84Kr, мы сохраняем нейтронную структуру каркаса 268Mt, но протонов в сверхзаполненном состоянии уже три.
Квазиоболочка 12 (110281???, 112283???, 114289???, 116289???)
Двенадцатая квазиоболочка является завершающей. Начинается она с ядра, имеющего заряд 110, и заканчивается, возможно, ядром с зарядом 120. Из экспериментов, проведенных в Дубне [15], следует существование 116 и 118 элементов.
110281???(5/2) (рис. 73). Если в качестве внутреннего кластера поместить 88Sr, образуется оболочка с 72 протонами (72 – магическое число) и 49 нейтронами. 116289??? (рис. 74). Два нейтрона из каркаса 114289??? превращаются в два протона. Дополнительные два протона размещаются в экваторе каркаса. В области экватора каркаса есть еще четыре протонные вакансии. А значит, есть шанс открыть 120 элемент.
Заключение
Таким образом, специфика формирования объемного каркаса из ядерных связок адекватно отражает капельные свойства ядра. Периодическое насыщение ядерных связок нуклонами вызывает появление новых ядерных связок, имеющих нуклоны в вертикальных узлах каркаса. Так как, в дважды магических ядрах каркас обладает максимальной симметрией и прочностью наличие нуклонной вакансии (или "лишнего" нуклона) не приводит к изменению расположения в нем других нуклонов. Следовательно, спин нуклона, находящийся в противоположном секторе каркаса, можно рассматривать как спин вакансии.
Проявление кластерных свойств ядра связано с тремя факторами:
- а) более плотным расположением нуклонов в узловых точках ядерных связок;
- б) наличием у ядер периферийных узловых точек с пониженной энергией связи;
- в) существованием у средних и тяжелых ядер в центре каркаса кластера из Ч-Ч ядер.
Следует заметить, что наличие каркаса решает не только проблему деформации ядра, но и задает алгоритм размещения нуклонов относительно друг друга и оси симметрии. Кроме того, это позволяет так же понять природу у некоторых ядер аномально большого спина.
- Фиксация нуклонов в узлах ядерного каркаса не противоречит принципу неопределенности т.к. это приводит к вибрациям всей поверхности ядра, т.е. к его температурному разогреву. На энергетический спектр вибрации поверхности ядра накладываются и другие типы возбуждений ядра. Как правило, они являются проявлением групповых возмущений нуклонов, что приводит к усилению амплитуды колебаний поверхности ядра.
Природа аналогии между ротационным спектром (1) и джозефсоновскими колебаниями (2) связана с деформацией ядерного каркаса. В данном случае деформационное напряжение каркаса эквивалентно постоянной разности потенциала между двумя состояниями нуклона, где высота энергетического барьера равна ε0 ≈ 6,7 MeV. Деформационное напряжение провоцирует периодический переход между протоном и нейтроном находящихся в одном из узловых кластеров каркаса. Перезарядка нуклона из-за принципа Паули, сопровождается колебаниями протона и нейтрона с характерным джозефсоновским спектром.
Для ядер с А>100, деформация ядерного каркаса задается деформацией внутреннего кластера, т.е. это результат внешнего воздействия на каркас ядра. У более легких ядер, обладающих внутренним кластером, жесткость ядерного каркаса еще мала, чтобы выдерживать вибрации связанные с перезарядкой нуклона.
Литература
- 1. Г.М. Амальский, ЯФ 56, 70, (1993).
- 2. Б.И. Барц, Е.В. Ипонин, М.И. Казаринов и др., Известия АН СССР, серия физ. 51, 1985 (1987).
- 3. В.М. Беленький, Э.И. Волмянский, Е.П. Григорьев, Т.Р. Дадамухамедов, Известия АН СССР, серия физ. 49, 72 (1985).
- 4. Д.А. Волков, А.И. Левон, Известия АН СССР, серия физ. 54, 2176 (1990).
- 5. А.К. Шевелев, Структура ядра, КомКнига, Москва (2006), ISBN 5-484-00480-2
- 6. Физические величины: справочник под ред. И.С. Григорьева, Е.З. Мейлихова, Энергоатомиздат, Москва (1991).
- 7. R.B. Firestone, Table of isotopes: In 2 vol / Ed.: v.s. Shirley. – 8 th ed. – New York.ttc.: John Wiley Sons. (1996).
- 8. Н. И. Волошин, Г.П. Палкин, А.Д. Фурса, В.Б. Шостак, Известия РАН, серия физ. 56, 93 (1992).
- 9. А.В. Юшков, ЭЧАЯ 24, 384 (1993).
- 10. Г.Ф. Филиппов, И.Ю. Рыбкин, С.В. Кореннов, Известия РАН, серия физ. 60, 46 1996).
- 11. К. Вильдермут, Я. Тан, Единая теория ядра, Мир, Москва (1980).
- 12. О.Ю. Балашова, Н.С. Зеленская, А.А. Овчинникова, Известия АН СССР, серия физ. 52, 2206 (1988).
- 13. А.В. Кулик, Известия РАН, серия физ. 62, 198 (1998).
- 14. В. Е. Митрошин, ЯФ 68, 1368 (2005).
- 15. Ю.Ц. Оганесян, ЯФ 63,1391 (2000).