
Интегральное исчисление, раздел математики, в котором изучаются свойства и способы вычисления интегралов и их приложения. И. и. тесно связано с дифференциальным исчислением и составляет вместе с ним одну из основных частей математического анализа (или анализа бесконечно малых). Центральными понятиями И. и. являются понятия определённого интеграла и неопределённого интеграла функций одного действительного переменного.
Определённый интеграл. Пусть требуется вычислить площадь S «криволинейной трапеции» — фигуры ABCD (см. рис.), ограниченной дугой непрерывной линии, уравнение которой у = f (x), отрезком AB оси абсцисс и двумя ординатами AD и BC. Для вычисления площади S этой криволинейной трапеции основание AB (отрезок [a, b]) разбивают на n участков (необязательно равных) точками а = x0 < x1 < ... < xn-1 < < xn = b, обозначая длины этих участков Dx1, Dx2, ..., Dxn; на каждом таком участке строят прямоугольники с высотами f (x1), f (x2), ..., f (xn) где xk — некоторая точка из отрезка [xk - 1, xk] (на рис. заштрихован прямоугольник, построенный на k-м участке разбиения; f (xk) — его высота). Сумма Sn площадей построенных прямоугольников рассматривается в качестве приближения к площади S криволинейной трапеции:
S » Sn = f (x1) Dx1 + f (x2) Dx2 + f (xn) Dxn
или, применяя для сокращения записи символ суммы S (греческая буква «сигма»):

Указанное выражение для площади криволинейной трапеции тем точнее, чем меньше длины Dxk участков разбиения. Для нахождения точного значения площади S надо найти предел сумм Sn в предположении, что число точек деления неограниченно увеличивается и наибольшая из длин Dxk стремится к нулю.
Отвлекаясь от геометрического содержания рассмотренной задачи, приходят к понятию определённого интеграла от функции f (x), непрерывной на отрезке [а, b], как к пределу интегральных сумм Sn при том же предельном переходе. Этот интеграл обозначается

Символ ò (удлинённое S — первая буква слова Summa) называется знаком интеграла, f (x) — подинтегральной функцией, числа а и b называются нижним и верхним пределами определённого интеграла. Если а = b, то, по определению, полагают

кроме того,

Свойства определённого интеграла:

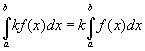
(k — постоянная). Очевидно также, что

(численное значение определённого интеграла не зависит от выбора обозначения переменной интегрирования).
К вычислению определённых интегралов сводятся задачи об измерении площадей, ограниченных кривыми (задачи «нахождения квадратур»), длин дуг кривых («спрямление кривых»), площадей поверхностей тел, объёмов тел («нахождение кубатур»), а также задачи определения координат центров тяжести, моментов инерции, пути тела по известной скорости движения, работы, производимой силой, и многие другие задачи естествознания и техники. Например, длина дуги плоской кривой, заданной уравнением у = f (x) на отрезке [a, b], выражается интегралом
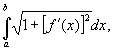
объём тела, образованного вращением этой дуги вокруг оси Ox,— интегралом
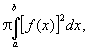
поверхность этого тела — интегралом
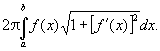
Фактическое вычисление определённых интегралов осуществляется различными способами. В отдельных случаях определённый интеграл можно найти, непосредственно вычисляя предел соответствующей интегральной суммы. Однако большей частью такой переход к пределу затруднителен. Некоторые определённые интегралы удаётся вычислять с помощью предварительного отыскания неопределённых интегралов (см. ниже). Как правило же, приходится прибегать к приближённому вычислению определённых интегралов, применяя различные квадратурные формулы (например, трапеций формулу, Симпсона формулу). Такое приближённое вычисление может быть осуществлено на ЭВМ с абсолютной погрешностью, не превышающей любого заданного малого положительного числа. В случаях, не требующих большой точности, для приближённого вычисления определённых интегралов применяют графические методы (см. Графические вычисления).
Понятие определённого интеграла распространяется на случай неограниченного промежутка интегрирования, а также на некоторые классы неограниченных функций. Такие обобщения называются несобственными интегралами.
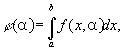
где функция f(x, a) непрерывна по x называются интегралами, зависящими от параметра. Они служат основным средством изучения многих специальных функций (см., например, Гамма-функция).
Неопределённый интеграл. Нахождение неопределённых интегралов, или интегрирование, есть операция, обратная дифференцированию. При дифференцировании данной функции ищется её производная. При интегрировании, наоборот, ищется первообразная (или примитивная) функция — такая функция, производная которой равна данной функции. Таким образом, функция F (x) является первообразной для данной функции f (x), если F'(x) = f (x) или, что то же самое, dF (x) = f (x) dx. Данная функция f (x) может иметь различные первообразные, но все они отличаются друг от друга только постоянными слагаемыми. Поэтому все первообразные для f (x) содержатся в выражении F (x) + С, которое называют неопределённым интегралом от функции f (x) и записывают
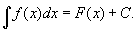
Определённый интеграл как функция верхнего предела интегрирования

(«интеграл с переменным верхним пределом»), есть одна из первообразных подинтегральной функции. Это позволяет установить основную формулу И. и. (формулу Ньютона — Лейбница):

выражающую численное значение определённого интеграла в виде разности значений какой-либо первообразной подинтегральной функции при верхнем и нижнем пределах интегрирования.
Взаимно обратный характер операций интегрирования и дифференцирования выражается равенствами

Отсюда следует возможность получения из формул и правил дифференцирования соответствующих формул и правил интегрирования (см. табл., где C, m, a, k — постоянные и m ¹ —1, а > 0).

¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾

¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾
Трудность И. и. по сравнению с дифференциальным исчислением заключается в том, что интегралы от элементарных функций не всегда выражаются через элементарные, могут не выражаться, как говорят, «в конечном виде». И. и. располагает лишь отдельными приёмами интегрирования в конечном виде, область применения каждого из которых ограничена (способы интегрирования излагаются в учебниках математического анализа: обширные таблицы интегралов приводятся во многих справочниках).
К классу функций, интегралы от которых всегда выражаются в элементарных функциях, принадлежит множество всех рациональных функций
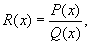
где P(x) и Q(x) — многочлены. Многие функции, не являющиеся рациональными, также интегрируются в конечном виде, например функции, рационально зависящие от

или же от x и рациональных степеней дроби

В конечном виде интегрируются и многие трансцендентные функции, например рациональные функции синуса и косинуса. Функции, которые изображаются неопределёнными интегралами, не берущимися в конечном виде, представляют собой новые трансцендентные функции. Многие из них хорошо изучены (см., например, Интегральный логарифм, Интегральный синус и интегральный косинус, Интегральная показательная функция).
Понятие интеграла распространяется на функции многих действительных переменных (см. Кратный интеграл, Криволинейный интеграл, Поверхностный интеграл), а также на функции комплексного переменного (см. Аналитические функции) и вектор-функции (см. Векторное исчисление).
О расширении и обобщении понятия интеграла см. ст. Интеграл.
Историческая справка. Возникновение задач И. и. связано с нахождением площадей и объёмов. Ряд задач такого рода был решен математиками Древней Греции. Античная математика предвосхитила идеи И. и. в значительно большей степени, чем дифференциального исчисления. Большую роль при решении таких задач играл исчерпывания метод, созданный Евдоксом Книдским и широко применявшийся Архимедом. Однако Архимед не выделил общего содержания интеграционных приёмов и понятия об интеграле, а тем более не создал алгоритма И. и. Учёные Среднего и Ближнего Востока в 9—15 вв. изучали и переводили труды Архимеда на общедоступный в их среде арабский язык, но существенно новых результатов в И. и. они не получили. Деятельность европейских учёных в это время была ещё более скромной. Лишь в 16 и 17 вв. развитие естественных наук поставило перед математикой Европы ряд новых задач, в частности задачи на нахождения квадратур, кубатур и определение центров тяжести. Труды Архимеда, впервые изданные в 1544 (на латинском и греческом языках), стали привлекать широкое внимание, и их изучение явилось одним из важнейших отправных пунктов дальнейшего развития И. и. Античный «неделимых» метод был возрожден И. Кеплером. В более общей форме идеи этого метода были развиты Б. Кавальери, Э. Торричелли, Дж. Валлисом, Б. Паскалем. Методом «неделимых» был решен ряд геометрических и механических задач. К этому же времени относятся опубликованные позднее работы П. Ферма по квадрированию парабол n-й степени, а затем — работы Х. Гюйгенса по спрямлению кривых.
В итоге этих исследований выявилась общность приёмов интегрирования при решении внешне несходных задач геометрии и механики, приводившихся к квадратурам как к геометрическому эквиваленту определённого интеграла. Заключительным звеном в цепи открытий этого периода было установление взаимно обратной связи между задачами на проведение касательной и на квадратуры, т. е. между дифференцированием и интегрированием. Основные понятия и алгоритм И. и. были созданы независимо друг от друга И. Ньютоном и Г. Лейбницем. Последнему принадлежит термин «интегральное исчисление» и обозначение интеграла òydx.
При этом в работах Ньютона основную роль играло понятие неопределённого интеграла (флюенты, см. Флюксий исчисление), тогда как Лейбниц исходил из понятия определённого интеграла. Дальнейшее развитие И. и. в 18 в. связано с именами И. Бернулли и особенно Л. Эйлера. В начале 19 в. И. и. вместе с дифференциальным исчислением было перестроено О. Коши на основе теории пределов. В развитии И. и. в 19 в. приняли участие русские математики М. В. Остроградский, В. Я. Буняковский, П. Л. Чебышев. В конце 19 — начале 20 вв. развитие теории множеств и теории функций действительного переменного привело к углублению и обобщению основных понятий И. и. (Б. Риман, А. Лебег и др.).
Лит.: История. Ван дер Варден Б. Л., Пробуждающаяся наука, пер. с голл., М., 1959; Вилейтнер Г., История математики от Декарта до середины 19 столетия, пер. с нем., 2 изд., М., 1966; Строек Д. Я., Краткий очерк истории математики, пер. с нем., 2 изд., М., 1969; Cantor М.. Vorleslingen über Geschichte der Mathematik, 2 Aufl., Bd 3—4, Lpz. — B., 1901—24.
Работы основоположников и классиков И. и. Ньютон И., Математические работы, пер. с латин., М.—Л., 1937; Лейбниц Г., Избранные отрывки из математических сочинений, пер. с. латин., «Успехи математических наук», 1948, т. 3, в. 1; Эйлер Л., Интегральное исчисление, пер. с латин., тт. 1—3, М., 1956—58; Коши О. Л., Краткое изложение уроков о дифференциальном и интегральном исчислении, пер. с франц., СПБ, 1831; его же, Алгебраический анализ, пер. с франц., Лейпциг, 1864.
Учебники и учебные пособия по И. и. Хинчин Д. Я., Краткий курс математического анализа, 3 изд., 1957; Смирнов В. И., Курс высшей математики, 22 изд., т. 1, М., 1967; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 2, М., 1969; Ильин В., Позняк Э. Г., Основы математического анализа, 3 изд., ч. 1, М., 1971; Курант Р., Курс дифференциального и интегрального исчисления, пер. с нем. и англ., 4 изд., т. 1, М., 1967; Двайт Г.-Б., Таблицы интегралов и другие математические формулы, пер. с англ., М., 1964.
Под редакцией академика А. Н. Колмогорова.

Рис. к ст. Интегральное исчисление.