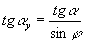 .
.Номография (от греч. nómos — закон и ...графия), раздел математики, объединяющий теорию и практические методы построения номограмм — специальных чертежей, являющихся изображениями функциональных зависимостей. Особенность номограмм заключается в том, что каждый чертёж изображает заданную область изменения переменных и каждое из значений переменных в этой области изображено на номограмме определённым геометрическим элементом (точкой или линией); изображения значения переменных, связанных функциональной зависимостью, находятся на номограмме в определённом соответствии, общем для номограмм одного и того же типа.
На рис. 1 приведён пример номограммы для вычисления ay — одного из углов установки резца на заточном станке по заданным значениям углов резца a и j Зависимость между этими величинами определяется формулой:
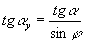 .
.
Номограмма состоит из трёх шкал: шкалы углов ay шкалы углов a и шкалы углов j. Точки каждой из шкал являются изображениями значения соответствующего переменного. Номограмма построена так, что три точки, изображающие соответственно значения ay, a и j, связанные данной зависимостью, всегда лежат на одной прямой. Отсюда непосредственно вытекает способ вычисления по номограмме: для вычисления ay надо на шкалах a и j найти точки, соответствующие данным значениям a и j, и через них провести прямую. Эта прямая пройдёт на шкале ay через точку, соответствующую искомому значению ay. На номограмме пунктирная линия соединяет точки шкал a и j со значениями a = 7,5° и j = 4°; номограмма даёт ответ ay = 62°.
Номограммы и их классификация. Номограммы различают по способу изображения переменных и по способу задания соответствия между изображениями переменных.
Изображения переменных. Значения переменных изображают на номограммах или точками, или линиями. Значение переменного, приписанное точке (линии), называется пометкой точки (линии), а сама точка (линия) называется помеченной точкой (линией). Область изменения переменного изображается на номограмме или совокупностью помеченных точек, которая называется шкалой переменного или однопараметрическим семейством помеченных линий. Для нахождения на шкале точек по их пометкам и значений пометок по заданным точкам шкалы градуируются системой штрихов, указывающих на отдельные точки шкалы. У некоторых штрихов надписываются значения пометок точек. Соответствие между точками шкалы, не отмеченными штрихами и их пометками, устанавливается линейной интерполяцией, которая выполняется на номограмме на глаз. В семействе линий проводят также лишь отдельные линии, остальные находят интерполяцией. При изображении значений переменных точками, наряду со шкалами, в номограммах применяют бинарные поля. Бинарное поле является изображением области изменения двух переменных и состоит из точек, каждой из которых поставлена в соответствие пара чисел — приписано две пометки: пометка первого переменного и пометка второго переменного. Точки бинарного поля заполняют двумерную область. В бинарном поле переменных и и v проводят два семейства линий u = const и n = const, которые позволяют по данным пометкам находить точку в поле и по точке поля её пометки (на рис. 3 это — вертикальные прямые h и кривые j). В нужных случаях здесь также применяют линейную интерполяцию.
Классификация номограмм. Наиболее распространены следующие номограммы: из выравненных точек, сетчатые и транспарантные; для уравнения с двумя переменными применяют двойные шкалы.
Двойная шкала является простейшим видом номограммы. Для уравнения F (u, n) = 0 она состоит из совмещенных шкал переменных u и n. Шкалы построены так, что их точки, пометки которых удовлетворяют уравнению, совпадают. На рис. 2 приведён пример двойной шкалы для вычисления логарифмов: u = lg n.
Номограмма из выравненных точек уравнения F (u, n, w) = 0 состоит из трёх шкал переменных u, n и w, изображающих соответственно область изменения этих переменных. Шкалы номограммы построены так, что три точки, пометки которых удовлетворяют уравнению, лежат на одной прямой (отсюда и название номограммы; пример номограммы из выравненных точек приведён на рис. 1). Номограмма из выравненных точек с бинарным полем уравнения F (u, n, w, t) = 0 с четырьмя переменными состоит из шкал переменных u и n и бинарного поля переменных w и t. Шкалы и поле номограммы построены так, что две точки с пометками u и n на шкалах и точка поля с двойной пометкой (w, t) лежат на одной прямой, если значения переменных u, n, w и t удовлетворяют уравнению.
Номограмма с двумя шкалами и бинарным полем приведена на рис. 3. Она служит для вычисления площади S равнобочной трапеции по длине b меньшего её основания, высоте h и углу j между большим основанием и боковой стороной:
S = bh + h2 ctg j.
Номограмма состоит из шкалы S, шкалы b и поля (j, h). Для нахождения S надо по данным h и j найти точку в поле, по данному b — точку на шкале и провести через эти точки прямую. Пометка точки пересечения прямой со шкалой S даёт ответ. На рисунке показан пунктиром пример, когда h = 8, j = 60° и b = 8; ответ: S = 100.
Номограмма из выравненных точек может содержать и два и три бинарных поля, т. е. одним приложением линейки давать решение уравнения и с пятью и с шестью переменными.
Сетчатая номограмма уравнения F (u, n, w) = 0 с тремя переменными u, n и w состоит из трёх семейств помеченных линий, изображающих соответственно данные области изменения этих переменных. Линии семейств построены так, что каждые три линии, пометки которых удовлетворяют уравнению, пересекаются в одной точке. На рис. 4 приведён пример сетчатой номограммы для определения необходимой реактивной мощности k на1 квт нагрузки электрич. установки для повышения её cos j от cos j1 до cos j2
k = tg j1 — tg j2.
Она состоит из семейства прямых, помеченных значениями существующего cos j1, семейства прямых, помеченных значениями k, и семейства кривых, помеченных значениями искомого cos j2. Для вычисления величины k по данным cos j1 и cos j2 надо найти на номограмме соответствующие линии и точку их пересечения. Пометка линии семейства k, проходящая через эту точку, даст ответ [так, для cos j1 = 0,8, cos j2 = 0,95 («отставание») находим k = 0,4].
При построении сетчатых номограмм может быть поставлена дополнительная задача: найти такое преобразование, при котором все три семейства линий номограммы обращаются в семейства прямых, что упрощает её вычерчивание. Такая задача носит название анаморфозы и эквивалентна задаче построения для данного уравнения номограммы из выравненных точек, так как посредством коррелятивного преобразования сетчатую номограмму из прямых можно перевести в номограмму из выравненных точек с тремя шкалами. Для построения сетчатых номограмм из прямых линий применяются т. н. функциональные сетки. Функциональная сетка представляет собой систему координатных линий (u, n) (часто изготовленную типографским способом), имеющих в декартовых координатах уравнения:
х = j1 (u), у = j2 (n).
Простейшими функциональными сетками являются логарифмическая и полулогарифмическая бумага (см. Логарифмическая бумага). Существуют также: сетка, на которой отрезками прямых изображаются части синусоиды; сетка для изображения нормального закона распределения вероятностей прямой линией (см. Вероятностная бумага) и т.п. Функциональные сетки применяются и при построении сетчатых номограмм, когда линии третьего семейства — кривые, но выглядят на сетке проще или нагляднее, чем в декартовой системе координат.
Транспарантная номограмма в простейшем случае состоит из двух плоскостей — основной плоскости и транспаранта с изображениями на них переменных в виде шкал, бинарных полей или семейств помеченных линий; основная плоскость и транспарант могут также содержать непомеченные («немые») линии и точки. Номограмма построена так, что элементы, помеченные значениями, удовлетворяющими уравнению, а также «немые» элементы номограммы при наложении транспаранта на основную плоскость должны в определённой последовательности вступать в контакты. Контактом двух элементов называется принадлежность их одного другому (точка лежит на линии, прямая касается линии и т.д.). Для практического осуществления необходимых контактов в нужных случаях транспарант делают из прозрачного материала.
На рис. 5 показана транспарантная номограмма для вычисления температуры t смеси двух жидкостей с одинаковой теплоёмкостью по формуле:
 ,
,
где m1 — масса с температурой t1, m2 — масса с температурой t2. Номограмма состоит из семейства параллельных прямых на основной плоскости номограммы и шкалы на транспаранте, оформленном в виде линейки. Прямые имеют пометки m1 — влево от средней прямой с пометкой 0 (на рис. 5 она выделена), и пометки m2 — вправо от средней прямой. Шкала транспаранта является одновременно шкалой переменных t1, t2 и t. Для вычисления по номограмме накладывают транспарант на основную плоскость так, чтобы точки, соответствующие данным m1 и m2, оказались на прямых, соответствующих данным t2 и t1, т. е. здесь осуществляется контакт между точкой t2 и прямой m1 и между точкой t1 и прямой t2. Ответом будет пометка точки пересечения шкалы t с прямой, имеющей пометку 0. В данном случае эта прямая играет роль «немого» элемента номограммы, вступающего в контакт с точкой ответной шкалы. На рис. 5 решен пример, когда m1 = 8 кг, t1 = 52°, m2 = 10 кг, t2 = 16°; ответ: t = 32°.
Примером транспарантной номограммы, транспарант которой имеет лишь поступат. движение, является логарифмическая линейка.
Составные номограммы. Для уравнений со многими переменными применяют составные номограммы, представляющие систему отд. номограмм, связанных общими шкалами или семействами линий. Обычно элементами составных номограмм являются номограммы из выравненных точек и сетчатые номограммы.
Погрешности вычислений по номограммам. Выполнение вычислений по номограммам сопровождается погрешностями, которые являются следствием невозможности (в процессе вычисления) точного осуществления необходимого соответствия между элементами номограммы.
Точность вычисления по номограммам существенно зависит от аккуратности выполнения необходимых операций. При вычислении по номограммам из выравненных точек следует применять прозрачную линейку с продольной визирной чертой.
Возможность представления уравнений номограммами. Номограммы разделяются на точные и приближённые.
Номограмма данной функциональной зависимости называется точной, если обусловленное её типом соответствие между изображениями переменных (в предположении точного осуществления) устанавливает между переменными зависимость, совпадающую с данной.
Условия точного номографирования налагают определённые ограничения на вид уравнений, для которых можно построить номограммы.
Условия, которым должно удовлетворять уравнение, для того чтобы можно было построить его номограмму, называются условиями номографируемости. При построении номограмм номографируемое уравнение преобразуется в одну из т. н. канонических форм, для которых известны в общем виде уравнения шкал, полей, семейств линий соответствующей номограммы.
При построении составных номограмм дополнительно необходимо представление данного уравнения со многими переменными в виде системы уравнений с меньшим числом переменных — т. н. разделение переменных (это достигается введением вспомогательных параметров).
Номограмма данной функциональной зависимости называется приближённой, если обусловленное типом номограммы соответствие между её элементами (в предположении точного его осуществления) устанавливает между переменными зависимость, приближённо представляющую данную. Создан ряд способов построения приближённых номограмм в основном типа из выравненных точек.
На рис. 6 изображена приближённая номограмма интегрального закона Стьюдента распределения вероятностей:
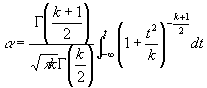 .
.
Погрешность в определении t за счёт приближённого номографирования в данной области изменения переменных а, k и t не превышает ± 0,001.
Приближённые номограммы применяют тогда, когда точные номограммы невозможны или когда точные номограммы имеют неудачную форму и дают большую погрешность в ответе.
Историческая справка. Геометрические изображения зависимостей между переменными, избавляющие от вычислений, известны давно. К ним можно отнести достаточно сложные построения, содержащие семейства линий и шкалы как изображения переменных (встречающиеся, например, в солнечных часах и астролябиях). Разработка теории номографических построений началась в 19 в. Первой была создана теория построения прямолинейных сетчатых номограмм (французский математик Л. Л. К. Лаланн, 1843). Основания общей теории номографических построений дал М. Окань в 1884—91; в его же работах впервые встречается название «Н.». Первым в России вопросами Н. начал заниматься Н. М. Герсеванов в 1906—08. Большая заслуга в деле развития теории Н. и организации номографирования инженерных расчётов принадлежит Н. А. Глаголеву, возглавлявшему советскую номографическую школу.
Лит.: Пентковский М. В., Считающие чертежи. (Номограммы), 2 изд., М., 1959; его же, Номография, М. — Л., 1949; Герсеванов Н. М., Основы номографии, 2 изд., М. — Л., 1932; Глаголев Н. А., Теоретические основы номографии, 2 изд., М. — Л., 1936; его же. Курс номографии, 2 изд., М., 1961; Невский Б. А., Справочная книга по номографии, М. — Л., 1951; Номографический сборник, М., 1951; D'Ocagne М., Traité de nomographie, 2 éd., P., 1921; Soureau R., Nomographie ou traité des abaques, t. 1—2, P., 1921.
М. В. Пентковский.

Рис. 2. Двойная шкала для вычисления логарифма (u) числа (v).

Рис. 1. Номограмма из выравненных точек для вычисления ay.

Рис. 6. Приближённая номограмма из выравненных точек интегрального закона Стьюдента распределения вероятностей.
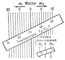
Рис. 5. Транспарантная номограмма для определения температуры смеси двух жидкостей с одинаковой теплоёмкостью.

Рис. 4. Сетчатая номограмма для вычисления мощности, потребной на 1 квт нагрузки электрической установки для перехода от cos j1 к cos j2.

Рис. 3. Номограмма из выравненных точек с бинарным полем для вычисления площади (S) равноблочной трапеции.