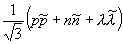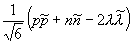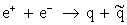Элементарные частицы.
Введение. Э. ч. в точном значении этого термина — первичные, далее неразложимые частицы, из которых, по предположению, состоит вся материя. В понятии «Э. ч.» в современной физике находит выражение идея о первообразных сущностях, определяющих все известные свойства материального мира, идея, зародившаяся на ранних этапах становления естествознания и всегда игравшая важную роль в его развитии.
Понятие «Э. ч.» сформировалось в тесной связи с установлением дискретного характера строения вещества на микроскопическом уровне. Обнаружение на рубеже 19—20 вв. мельчайших носителей свойств вещества — молекул и атомов — и установление того факта, что молекулы построены из атомов, впервые позволило описать все известные вещества как комбинации конечного, хотя и большого, числа структурных составляющих — атомов. Выявление в дальнейшем наличия составных слагающих атомов — электронов и ядер, установление сложной природы ядер, оказавшихся построенными всего из двух типов частиц (протонов и нейтронов), существенно уменьшило количество дискретных элементов, формирующих свойства вещества, и дало основание предполагать, что цепочка составных частей материи завершается дискретными бесструктурными образованиями — Э. ч. Такое предположение, вообще говоря, является экстраполяцией известных фактов и сколько-нибудь строго обосновано быть не может. Нельзя с уверенностью утверждать, что частицы, элементарные в смысле приведённого определения, существуют. Протоны и нейтроны, например, длительное время считавшиеся Э. ч., как выяснилось, имеют сложное строение. Не исключена возможность того, что последовательность структурных составляющих материи принципиально бесконечна. Может оказаться также, что утверждение «состоит из...» на какой-то ступени изучения материи окажется лишённым содержания. От данного выше определения «элементарности» в этом случае придется отказаться. Существование Э. ч. — это своего рода постулат, и проверка его справедливости — одна из важнейших задач физики.
Термин «Э. ч.» часто употребляется в современной физике не в своём точном значении, а менее строго — для наименования большой группы мельчайших частиц материи, подчинённых условию, что они не являются атомами или атомными ядрами (исключение составляет простейшее ядро атома водорода — протон). Как показали исследования, эта группа частиц необычайно обширна. Помимо упоминавшихся протона (р), нейтрона (n) и электрона (e-) к ней относятся: фотон (g), пи-мезоны (p), мюоны (m), нейтрино трёх типов (электронное ve, мюонное vm и связанное с т. н. тяжёлым лептоном vt), т. н. странные частицы (К-мезоны и гипероны), разнообразные резонансы, открытые в 1974—77 y-частицы, «очарованные» частицы, ипсилон-частицы (¡) и тяжёлые лептоны (t+, t—) — всего более 350 частиц, в основном нестабильных. Число частиц, включаемых в эту группу, продолжает расти и, скорее всего, неограниченно велико; при этом большинство перечисленных частиц не удовлетворяет строгому определению элементарности, поскольку, по современным представлениям, они являются составными системами (см. ниже). Использование названия «Э. ч.» ко всем этим частицам имеет исторические причины и связано с тем периодом исследований (начало 30-х гг. 20 в.), когда единственно известными представителями данной группы были протон, нейтрон, электрон и частица электромагнитного поля — фотон. Эти четыре частицы тогда естественно было считать элементарными, т. к. они служили основой для построения окружающего нас вещества и взаимодействующего с ним электромагнитного поля, а сложная структура протона и нейтрона не была известна.
Открытие новых микроскопических частиц материи постепенно разрушило эту простую картину. Вновь обнаруженные частицы, однако, во многих отношениях были близки к первым четырём известным частицам. Объединяющее их свойство заключается в том, что все они являются специфическими формами существования материи, не ассоциированной в ядра и атомы (иногда по этой причине их называют «субъядерными частицами»). Пока количество таких частиц было не очень велико, сохранялось убеждение, что они играют фундаментальную роль в строении материи, и их относили к категории Э. ч. Нарастание числа субъядерных частиц, выявление у многих из них сложного строения показало, что они, как правило, не обладают свойствами элементарности, но традиционное название «Э. ч.» за ними сохранилось.
В соответствии со сложившейся практикой термин «Э. ч.» будет употребляться ниже в качестве общего назв. субъядерных частиц. В тех случаях, когда речь будет идти о частицах, претендующих на роль первичных элементов материи, при необходимости будет использоваться термин «истинно Э. ч.».
Краткие исторические сведения. Открытие Э. ч. явилось закономерным результатом общих успехов в изучении строения вещества, достигнутых физикой в конце 19 в. Оно было подготовлено всесторонними исследованиями оптических спектров атомов, изучением электрических явлений в жидкостях и газах, открытием фотоэлектричества, рентгеновских лучей, естественной радиоактивности, свидетельствовавших о существовании сложной структуры материи.
Исторически первой открытой Э. ч. был электрон — носитель отрицательного элементарного электрического заряда в атомах. В 1897 Дж. Дж. Томсон установил, что т. н. катодные лучи образованы потоком мельчайших частиц, которые были названы электронами. В 1911 Э. Резерфорд, пропуская альфа-частицы от естественного радиоактивного источника через тонкие фольги различных веществ, выяснил, что положительный заряд в атомах сосредоточен в компактных образованиях — ядрах, а в 1919 обнаружил среди частиц, выбитых из атомных ядер, протоны — частицы с единичным положительным зарядом и массой, в 1840 раз превышающей массу электрона. Другая частица, входящая в состав ядра, — нейтрон — была открыта в 1932 Дж. Чедвиком при исследованиях взаимодействия a-частиц с бериллием. Нейтрон имеет массу, близкую к массе протона, но не обладает электрическим зарядом. Открытием нейтрона завершилось выявление частиц — структурных элементов атомов и их ядер.
Вывод о существовании частицы электромагнитного поля — фотона — берёт своё начало с работы М. Планка (1900). Предположив, что энергия электромагнитного излучения абсолютно чёрного тела квантованна, Планк получил правильную формулу для спектра излучения. Развивая идею Планка, А. Эйнштейн (1905) постулировал, что электромагнитное излучение (свет) в действительности является потоком отдельных квантов (фотонов), и на этой основе объяснил закономерности фотоэффекта. Прямые экспериментальные доказательства существования фотона были даны Р. Милликеном (1912— 1915) и А. Комптоном (1922; см. Комптона эффект).
Открытие нейтрино — частицы, почти не взаимодействующей с веществом, ведёт своё начало от теоретической догадки В. Паули (1930), позволившей за счёт предположения о рождении такой частицы устранить трудности с законом сохранения энергии в процессах бета-распада радиоактивных ядер. Экспериментально существование нейтрино было подтверждено лишь в 1953 (Ф. Райнес и К Коуэн, США).
С 30-х и до начала 50-х гг. изучение Э. ч. было тесно связано с исследованием космических лучей. В 1932 в составе космических лучей К. Андерсоном был обнаружен позитрон (е+) — частица с массой электрона, но с положительным электрическим зарядом. Позитрон был первой открытой античастицей (см. ниже). Существование е+ непосредственно вытекало из релятивистской теории электрона, развитой П. Дираком (1928—31) незадолго до обнаружения позитрона. В 1936 американские физики К. Андерсон и С. Неддермейер обнаружили при исследовании осмических лучей мюоны (обоих знаков электрического заряда) — частицы с массой примерно в 200 масс электрона, а в остальном удивительно близкие по свойствам к е-, е+.
В 1947 также в космических лучах группой С. Пауэлла были открыты p+ и p--мезоны с массой в 274 электронные массы, играющие важную роль во взаимодействии протонов с нейтронами в ядрах. Существование подобных частиц было предположено Х. Юкавой в 1935.
Конец 40-х — начало 50-х гг. ознаменовались открытием большой группы частиц с необычными свойствами, получивших название «странных». Первые частицы этой группы К+- и К--мезоны, L-, S+ -, S- -, X- -гипероны были открыты в космических лучах, последующие открытия странных частиц были сделаны на ускорителях — установках, создающих интенсивные потоки быстрых протонов и электронов. При столкновении с веществом ускоренные протоны и электроны рождают новые Э. ч., которые и становятся предметом изучения.
С начала 50-х гг. ускорители превратились в основной инструмент для исследования Э. ч. В 70-х гг. энергии частиц, разогнанных на ускорителях, составили десятки и сотни млрд. электронвольт (Гэв). Стремление к увеличению энергий частиц обусловлено тем, что высокие энергии открывают возможность изучения строения материи на тем меньших расстояниях, чем выше энергия сталкивающихся частиц. Ускорители существенно увеличили темп получения новых данных и в короткий срок расширили и обогатили наше знание свойств микромира. Применение ускорителей для изучения странных частиц позволило более детально изучить их свойства, в частности особенности их распада, и вскоре привело к важному открытию: выяснению возможности изменения характеристик некоторых микропроцессов при операции зеркального отражения (см. Пространственная инверсия) — т. н. нарушению пространств. чётности (1956). Ввод в строй протонных ускорителей с энергиями в миллиарды эв позволил открыть тяжёлые античастицы: антипротон (1955), антинейтрон (1956), антисигма-гипероны (1960). В 1964 был открыт самый тяжёлый гиперон W- (с массой около двух масс протона). В 1960-х гг. на ускорителях было открыто большое число крайне неустойчивых (по сравнению с др. нестабильными Э. ч.) частиц, получивших название «резонансов». Массы большинства резонансов превышают массу протона. Первый из них D1 (1232) был известен с 1953. Оказалось, что резонансы составляют основная часть Э. ч.
В 1962 было выяснено, что существуют два разных нейтрино: электронное и мюонное. В 1964 в распадах нейтральных К-мезонов. было обнаружено несохранение т, н. комбинированной чётности (введённой Ли Цзун-дао и Ян Чжэнь-нином и независимо Л. Д. Ландау в 1956; см. Комбинированная инверсия), означающее необходимость пересмотра привычных взглядов на поведение физических процессов при операции отражения времени (см. Теорема СРТ).
В 1974 были обнаружены массивные (в 3—4 протонные массы) и в то же время относительно устойчивые y-частицы, с временем жизни, необычно большим для резонансов. Они оказались тесно связанными с новым семейством Э. ч. — «очарованных», первые представители которого (D0, D+, Lс) были открыты в 1976. В 1975 были получены первые сведения о существовании тяжёлого аналога электрона и мюона (тяжёлого лептона t). В 1977 были открыты ¡-частицы с массой порядка десятка протонных масс.
Таким образом, за годы, прошедшие после открытия электрона, было выявлено огромное число разнообразных микрочастиц материи. Мир Э. ч. оказался достаточно сложно устроенным. Неожиданными во многих отношениях оказались свойства обнаруженных Э. ч. Для их описания, помимо характеристик, заимствованных из классической физики, таких, как электрический заряд, масса, момент количества движения, потребовалось ввести много новых специальных характеристик, в частности для описания странных Э. ч. — странность (К. Нишиджима, М. Гелл-Ман, 1953), «очарованных» Э. ч. — «очарование» (американские физики Дж. Бьёркен, Ш. Глэшоу, 1964); уже названия приведённых характеристик отражают необычность описываемых ими свойств Э. ч.
Изучение внутреннего строения материи и свойств Э. ч. с первых своих шагов сопровождалось радикальным пересмотром многих устоявшихся понятий и представлений. Закономерности, управляющие поведением материи в малом, оказались настолько отличными от закономерностей классической механики и электродинамики, что потребовали для своего описания совершенно новых теоретических построений. Такими новыми фундаментальными построениями в теории явились частная (специальная) и общая теория относительности (А. Эйнштейн, 1905 и 1916; см. Относительности теория, Тяготение) и квантовая механика (1924—27; Н. Бор, Л. де Бройль, В. Гейзенберг, Э. Шрёдингер, М. Борн). Теория относительности и квантовая механика знаменовали собой подлинную революцию в науке о природе и заложили основы для описания явлений микромира. Однако для описания процессов, происходящих с Э. ч., квантовой механики оказалось недостаточно. Понадобился следующий шаг — квантование классических полей (т. н. квантование вторичное) и разработка квантовой теории поля. Важнейшими этапами на пути её развития были: формулировка квантовой электродинамики (П. Дирак, 1929), квантовой теории b-распада (Э. Ферми, 1934), положившей начало современной теории слабых взаимодействий, квантовой мезодинамики (Юкава, 1935). Непосредственной предшественницей последней была т. н. b-теория ядерных сил (И. Е. Тамм, Д. Д. Иваненко, 1934; см. Сильные взаимодействия). Этот период завершился созданием последовательного вычислительного аппарата квантовой электродинамики (С. Томонага, Р. Фейнман, Ю. Швингер; 1944—49), основанного на использовании техники перенормировки (см. Квантовая теория поля). Эта техника была обобщена впоследствии применительно к другим вариантам квантовой теории поля.
Квантовая теория поля продолжает развиваться и совершенствоваться и является основой для описания взаимодействий Э. ч. У этой теории имеется ряд существенных успехов, и всё же она ещё очень далека от завершённости и не может претендовать на роль всеобъемлющей теории Э. ч. Происхождение многих свойств Э. ч. и природа присущих им взаимодействий в значительной мере остаются неясными. Возможно, понадобится ещё не одна перестройка всех представлений и гораздо более глубокое понимание взаимосвязи свойств микрочастиц и геометрических свойств пространства-времени, прежде чем теория Э. ч. будет построена.
Основные свойства элементарных частиц. Классы взаимодействий. Все Э. ч. являются объектами исключительно малых масс и размеров. У большинства из них массы имеют порядок величины массы протона, равной 1,6×10-24 г (заметно меньше лишь масса электрона: 9×10-28 г). Определённые из опыта размеры протона, нейтрона, p-мезона по порядку величины равны 10-13 см. Размеры электрона и мюона определить не удалось, известно лишь, что они меньше 10-15 см. Микроскопические массы и размеры Э. ч. лежат в основе квантовой специфики их поведения. Характерные длины волн, которые следует приписать Э. ч. в квантовой теории ( , где
, где  — постоянная Планка, m — масса частицы, с — скорость света) по порядку величин близки к типичным размерам, на которых осуществляется их взаимодействие (например, для p-мезона
— постоянная Планка, m — масса частицы, с — скорость света) по порядку величин близки к типичным размерам, на которых осуществляется их взаимодействие (например, для p-мезона  1,4×10-13 см). Это и приводит к тому, что квантовые закономерности являются определяющими для Э. ч.
1,4×10-13 см). Это и приводит к тому, что квантовые закономерности являются определяющими для Э. ч.
Наиболее важное квантовое свойство всех Э. ч. — их способность рождаться и уничтожаться (испускаться и поглощаться) при взаимодействии с др. частицами. В этом отношении они полностью аналогичны фотонам. Э. ч. — это специфические кванты материи, более точно — кванты соответствующих физических полей (см. ниже). Все процессы с Э. ч. протекают через последовательность актов их поглощения и испускания. Только на этой основе можно понять, например, процесс рождения p+-мезона при столкновении двух протонов (р + р ® р + n+ p+) или процесс аннигиляции электрона и позитрона, когда взамен исчезнувших частиц возникают, например, два g-кванта (е+ +е- ® g + g). Но и процессы упругого рассеяния частиц, например е- +p ® е- + р, также связаны с поглощением начальных частиц и рождением конечных частиц. Распад нестабильных Э. ч. на более лёгкие частицы, сопровождаемый выделением энергии, отвечает той же закономерности и является процессом, в котором продукты распада рождаются в момент самого распада и до этого момента не существуют. В этом отношении распад Э. ч. подобен распаду возбуждённого атома на атом в основном состоянии и фотон. Примерами распадов Э. ч. могут служить:  ; p+ ® m+ + vm; К+ ® p+ + p0 (знаком «тильда» над символом частицы здесь и в дальнейшем помечены соответствующие античастицы).
; p+ ® m+ + vm; К+ ® p+ + p0 (знаком «тильда» над символом частицы здесь и в дальнейшем помечены соответствующие античастицы).
Различные процессы с Э. ч. заметно отличаются по интенсивности протекания. В соответствии с этим взаимодействия Э. ч. можно феноменологически разделить на несколько классов: сильные, электромагнитные и слабые взаимодействия. Все Э. ч. обладают, кроме того, гравитационным взаимодействием.
Сильные взаимодействия выделяются как взаимодействия, которые порождают процессы, протекающие с наибольшей интенсивностью среди всех остальных процессов. Они приводят и к самой сильной связи Э. ч. Именно сильные взаимодействия обусловливают связь протонов и нейтронов в ядрах атомов и обеспечивают исключительную прочность этих образований, лежащую в основе стабильности вещества в земных условиях.
Электромагнитные взаимодействия характеризуются как взаимодействия, в основе которых лежит связь с электромагнитным полем. Процессы, обусловленные ими, менее интенсивны, чем процессы сильных взаимодействий, а порождаемая ими связь Э. ч. заметно слабее. Электромагнитные взаимодействия, в частности, ответственны за связь атомных электронов с ядрами и связь атомов в молекулах.
Слабые взаимодействия, как показывает само название, вызывают очень медленно протекающие процессы с Э. ч. Иллюстрацией их малой интенсивности может служить тот факт, что нейтрино, обладающие только слабыми взаимодействиями, беспрепятственно пронизывают, например, толщу Земли и Солнца. Слабые взаимодействия обусловливают также медленные распады т. н. квазистабильных Э. ч. Времена жизни этих частиц лежат в диапазоне 10-8—10-10 сек, тогда как типичные времена для сильных взаимодействий Э. ч. составляют 10-23—10-24 сек.
Гравитационные взаимодействия, хорошо известные по своим макроскопическим проявлениям, в случае Э. ч. на характерных расстояниях ~10-13 см дают чрезвычайно малые эффекты из-за малости масс Э. ч.
Силу различных классов взаимодействий можно приближённо охарактеризовать безразмерными параметрами, связанными с квадратами констант соответствующих взаимодействий. Для сильных, электромагнитных, слабых и гравитационных взаимодействий протонов при средней энергии процесса ~1 Гэв эти параметры соотносятся как 1:10-2: l0-10:10-38. Необходимость указания средней энергии процесса связана с тем, что для слабых взаимодействий безразмерный параметр зависит от энергии. Кроме того, сами интенсивности различных процессов по-разному зависят от энергии. Это приводит к тому, что относительная роль различных взаимодействий, вообще говоря, меняется с ростом энергии взаимодействующих частиц, так что разделение взаимодействий на классы, основанное на сравнении интенсивностей процессов, надёжно осуществляется при не слишком высоких энергиях. Разные классы взаимодействий имеют, однако, и другую специфику, связанную с различными свойствами их симметрии (см. Симметрия в физике), которая способствует их разделению и при более высоких энергиях. Сохранится ли такое деление взаимодействий на классы в пределе самых больших энергий, пока остаётся неясным.
В зависимости от участия в тех или иных видах взаимодействий все изученные Э. ч., за исключением фотона, разбиваются на две основные группы: адроны (от греческого hadros — большой, сильный) и лептоны (от греческого leptos — мелкий, тонкий, лёгкий). Адроны характеризуются прежде всего тем, что они обладают сильными взаимодействиями, наряду с электромагнитными и слабыми, тогда как лептоны участвуют только в электромагнитных и слабых взаимодействиях. (Наличие общих для той и другой группы гравитационных взаимодействий подразумевается.) Массы адронов по порядку величины близки к массе протона (тр); минимальную массу среди адронов имеет p-мезон: тp»м 1/7×тр. Массы лептонов, известных до 1975—76, были невелики ( 0,1 mp), однако новейшие данные, видимо, указывают на возможность существования тяжёлых лептонов с такими же массами, как у адронов. Первыми исследованными представителями адронов были протон и нейтрон, лептонов — электрон. Фотон, обладающий только электромагнитными взаимодействиями, не может быть отнесён ни к адронам, ни к лептонам и должен быть выделен в отд. группу. По развиваемым в 70-х гг. представлениям фотон (частица с нулевой массой покоя) входит в одну группу с очень массивными частицами — т. н. промежуточными векторными бозонами, ответственными за слабые взаимодействия и пока на опыте не наблюдавшимися (см. раздел Элементарные частицы и квантовая теория поля).
0,1 mp), однако новейшие данные, видимо, указывают на возможность существования тяжёлых лептонов с такими же массами, как у адронов. Первыми исследованными представителями адронов были протон и нейтрон, лептонов — электрон. Фотон, обладающий только электромагнитными взаимодействиями, не может быть отнесён ни к адронам, ни к лептонам и должен быть выделен в отд. группу. По развиваемым в 70-х гг. представлениям фотон (частица с нулевой массой покоя) входит в одну группу с очень массивными частицами — т. н. промежуточными векторными бозонами, ответственными за слабые взаимодействия и пока на опыте не наблюдавшимися (см. раздел Элементарные частицы и квантовая теория поля).
Характеристики элементарных частиц. Каждая Э. ч., наряду со спецификой присущих ей взаимодействий, описывается набором дискретных значений определённых физических величин, или своими характеристиками. В ряде случаев эти дискретные значения выражаются через целые или дробные числа и некоторый общий множитель — единицу измерения; об этих числах говорят как о квантовых числах Э. ч. и задают только их, опуская единицы измерения.
Общими характеристиками всех Э. ч. являются масса (m), время жизни (t), спин (J) и электрический заряд (Q). Пока нет достаточного понимания того, по какому закону распределены массы Э. ч. и существует ли для них какая-то единица измерения.
В зависимости от времени жизни Э. ч. делятся на стабильные, квазистабильные и нестабильные (резонансы). Стабильными, в пределах точности современных измерений, являются электрон (t > 5×1021 лет), протон (t > 2×1030 лет), фотон и нейтрино. К квазистабильным относят частицы, распадающиеся за счёт электромагнитных и слабых взаимодействий. Их времена жизни > 10-20 сек (для свободного нейтрона даже ~ 1000 сек). Резонансами называются Э. ч., распадающиеся за счёт сильных взаимодействий. Их характерные времена жизни 10-23—10-24 сек. В некоторых случаях распад тяжёлых резонансов (с массой ³ 3 Гэв) за счёт сильных взаимодействий оказывается подавленным и время жизни увеличивается до значений — ~10-20 сек.
Спин Э. ч. является целым или полуцелым кратным от величины  . В этих единицах спин p- и К-мезонов равен 0, у протона, нейтрона и электрона J= 1/2, у фотона J = 1. Существуют частицы и с более высоким спином. Величина спина Э. ч. определяет поведение ансамбля одинаковых (тождественных) частиц, или их статистику (В. Паули, 1940). Частицы полуцелого спина подчиняются Ферми — Дирака статистике (отсюда название фермионы), которая требует антисимметрии волновой функции системы относительно перестановки пары частиц (или нечётного числа пар) и, следовательно, «запрещает» двум частицам полуцелого спина находиться в одинаковом состоянии (Паули принцип). Частицы целого спина подчиняются Бозе — Эйнштейна статистике (отсюда название бозоны), которая требует симметрии волновой функции относительно перестановок частиц и допускает нахождение любого числа частиц в одном и том же состоянии. Статистические свойства Э. ч. оказываются существенными в тех случаях, когда при рождении или распаде образуется несколько одинаковых частиц. Статистика Ферми — Дирака играет также исключительно важную роль в структуре ядер и определяет закономерности заполнения электронами атомных оболочек, лежащие в основе периодической системы элементов Д. И. Менделеева.
. В этих единицах спин p- и К-мезонов равен 0, у протона, нейтрона и электрона J= 1/2, у фотона J = 1. Существуют частицы и с более высоким спином. Величина спина Э. ч. определяет поведение ансамбля одинаковых (тождественных) частиц, или их статистику (В. Паули, 1940). Частицы полуцелого спина подчиняются Ферми — Дирака статистике (отсюда название фермионы), которая требует антисимметрии волновой функции системы относительно перестановки пары частиц (или нечётного числа пар) и, следовательно, «запрещает» двум частицам полуцелого спина находиться в одинаковом состоянии (Паули принцип). Частицы целого спина подчиняются Бозе — Эйнштейна статистике (отсюда название бозоны), которая требует симметрии волновой функции относительно перестановок частиц и допускает нахождение любого числа частиц в одном и том же состоянии. Статистические свойства Э. ч. оказываются существенными в тех случаях, когда при рождении или распаде образуется несколько одинаковых частиц. Статистика Ферми — Дирака играет также исключительно важную роль в структуре ядер и определяет закономерности заполнения электронами атомных оболочек, лежащие в основе периодической системы элементов Д. И. Менделеева.
Электрические заряды изученных Э. ч. являются целыми кратными от величины е » 1,6×10-19 к, называются элементарным электрическим зарядом. У известных Э. ч. Q = 0, ±1, ±2.
Помимо указанных величин Э. ч. дополнительно характеризуются ещё рядом квантовых чисел, называются внутренними. Лептоны несут специфический лептонный заряд L двух типов: электронный (Le) и мюонный (Lm); Le = +1 для электрона и электронного нейтрино, Lm= +1 для отрицательного мюона и мюонного нейтрино. Тяжёлый лептон t; и связанное с ним нейтрино, по-видимому, являются носителями нового типа лептонного заряда Lt.
Для адронов L = 0, и это ещё одно проявление их отличия от лептонов. В свою очередь, значительные части адронов следует приписать особый барионный заряд В (|Е| = 1). Адроны с В = +1 образуют подгруппу барионов (сюда входят протон, нейтрон, гипероны, барионные резонансы), а адроны с В = 0 — подгруппу мезонов (p- и К-мезоны, бозонные резонансы). Название подгрупп адронов происходит от греческих слов barýs — тяжёлый и mésos — средний, что на начальном этапе исследований Э. ч. отражало сравнительные величины масс известных тогда барионов и мезонов. Более поздние данные показали, что массы барионов и мезонов сопоставимы. Для лептонов В = 0. Для фотона В = 0 и L = 0.
Барионы и мезоны подразделяются на уже упоминавшиеся совокупности: обычных (нестранных) частиц (протон, нейтрон, p-мезоны), странных частиц (гипероны, К-мезоны) и очарованных частиц. Этому разделению отвечает наличие у адронов особых квантовых чисел: странности S и очарования (английское charm) Ch с допустимыми значениями: 151 = 0, 1, 2, 3 и |Ch| = 0, 1, 2, 3. Для обычных частиц S = 0 и Ch = 0, для странных частиц |S| ¹ 0, Ch = 0, для очарованных частиц |Ch| ¹ 0, а |S| = 0, 1, 2. Вместо странности часто используется квантовое число гиперзаряд Y = S + В, имеющее, по-видимому, более фундаментальное значение.
Уже первые исследования с обычными адронами выявили наличие среди них семейств частиц, близких по массе, с очень сходными свойствами по отношению к сильным взаимодействиям, но с различными значениями электрического заряда. Протон и нейтрон (нуклоны) были первым примером такого семейства. Позднее аналогичные семейства были обнаружены среди странных и (в 1976) среди очарованных адронов. Общность свойств частиц, входящих в такие семейства, является отражением существования у них одинакового значения специального квантового числа — изотопического спина I, принимающего, как и обычный спин, целые и полуцелые значения. Сами семейства обычно называются изотопическими мультиплетами. Число частиц в мультиплете (п) связано с I соотношением: n = 2I + 1. Частицы одного изотопического мультиплета отличаются друг от друга значением «проекции» изотопического спина I3, и соответствующие значения Q даются выражением:

Важной характеристикой адронов является также внутренняя чётность Р, связанная с операцией пространств, инверсии: Р принимает значения ±1.
Для всех Э. ч. с ненулевыми значениями хотя бы одного из зарядов О, L, В, Y (S) и очарования Ch существуют античастицы с теми же значениями массы т, времени жизни t, спина J и для адронов изотопического спина 1, но с противоположными знаками всех зарядов и для барионов с противоположным знаком внутренней чётности Р. Частицы, не имеющие античастиц, называются абсолютно (истинно) нейтральными. Абсолютно нейтральные адроны обладают специальным квантовым числом — зарядовой чётностью (т. е. чётностью по отношению к операции зарядового сопряжения) С со значениями ±1; примерами таких частиц могут служить фотон и p0.
Квантовые числа Э. ч. разделяются на точные (т. е. такие, которые связаны с физическими величинами, сохраняющимися во всех процессах) и неточные (для которых соответствующие физические величины в части процессов не сохраняются). Спин J связан со строгим законом сохранения момента количества движения и потому является точным квантовым числом. Другие точные квантовые числа: Q, L, В; по современным данным, они сохраняются при всех превращениях Э. ч. Стабильность протона есть непосредственное выражение сохранения В (нет, например, распада р ® е+ + g). Однако большинство квантовых чисел адронов неточные. Изотопический спин, сохраняясь в сильных взаимодействиях, не сохраняется в электромагнитных и слабых взаимодействиях. Странность и очарование сохраняются в сильных и электромагнитных взаимодействиях, но не сохраняются в слабых взаимодействиях. Слабые взаимодействия изменяют также внутреннюю и зарядовую чётности. С гораздо большей степенью точности сохраняется комбинированная чётность СР, однако и она нарушается в некоторых процессах, обусловленных слабыми взаимодействиями. Причины, вызывающие несохранение многих квантовых чисел адронов, неясны и, по-видимому, связаны как с природой этих квантовых чисел, так и с глубинной структурой электромагнитных и слабых взаимодействий. Сохранение или несохранение тех или иных квантовых чисел — одно из существенных проявлений различий классов взаимодействий Э. ч.
Табл. 1. — Основные элементарные частицы и их характеристики
| Частица | Античастица | Масса, Мэв | J P | I, Y, Ch | Время жизни, сек, ширина, Мэв (*) |
| Фотон |
| g | 0 | 1- | — | стабилен |
| Лептоны |
| e- | e+ | 0,511003(1) | ½ | — | стабильны |
| n | ñe | 0(<3 ×10-5) | ½ | — | стабильны |
| m- | m+ | 105,6595(3) | ½ | — | 2,19713(7)×10-6 |
| n | ñm | 0(<0,4) | ½ | — | стабильны |
| t- | t+ | 1900(100) | ½ | — | ? |
| n | ñt | <600 | ½ | — | ? |
| Мезоны (В=0) |
| | p+ | | p- | 
| 0- | ö | 1,0,0 | 2,603(2)×10-8 |
| | | p0 | | | | 0,83(6)×10-16 |
| * | r+ | r0 | r- | 773(3) | 1- | | | 152(3) |
| * | B+ | B0 | B- | 1230(10) | 1+ | | | 125(10) |
| * | 
| 
| 
| 1310(5) | 2+ | ý | 102(5) |
| * | r’+ | r’0 | r’- | 1600 | 1- | | | ~400 |
| * | g+ | g0 | g- | 1690(20) | 3- | | | 180(30) |
| * | S+ | S0 | S- | 1940 | 4+ | ø | 54 |
| | h | | 548,8(6) | 0- | ö | 0,0,0 | 7(1)×10-19 |
| * | w | | 782,7(3) | 1- | | | 10,0(4) |
| * | h’ | | 957,6(3) | 0- | | | <1 |
| * | j | | 1019,7(3) | 1- | | | 4,1(2) |
| * | f | | 1270(5) | 2+ | | | 180(20) |
| * | f’ | | 1516(3) | 2+ | | | 40(10) |
| * | w’ | | 1667(10) | 3- | | | 140(10) |
| * | h | | 2020(25) | 4+ | ý | 180(50) |
| * | hc | | 2820(20) | 0-? | | | ? |
| * | y | | 3095(4) | 1- | | | 0,069(15) |
| * | y’ | | 3684(5) | 1- | | | 0,228(56) |
| * | y’’ | | 3772(6) | 1- | | | 28(5) |
| * | y’’’ | | 4414(7) | 1- | | | 33(10) |
| * | ¡ | | 9410(10) | 1-? | | | ? |
| * | ¡’ | | 10060(30) | 1-? | ø | ? |
| | | 
| 
| | 493,71(4) | 0 | ö | ½,1,0 | 1,237(3)×10-8 |
| | | 
| | 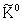
| 497,7(1) | | | 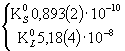
|
| | |
| * | 
| 
| 
| 
| 892,2(5) | 1 | ý | 50(1) |
| * | 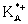
| 
| 
| 
| 1242(10) | 1 | | | 127(25) |
| * | 
| 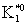
| 
| 
| 1421(3) | 2 | | | 100(10) |
| * | 
| 
| 
| 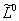
| 1765(10) | ? | ø | 140(50) |
| * | 
| | 
| | 1868,4(9) | 0- | ö | ½,-⅓,1 | ? |
| | | 
| | 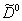
| 1863,3(9) | 0- | ý | ? |
| * | 
| | 
| | 2009(1) | 1- | | | ? |
| * | | 
| | 
| 2006(1,5) | 1- | ø | ? |
| Барионы (ïВ÷=1) |
| | p | | p̃ | | 
| ½+ | ö | ½,1,0 | стабильны |
| | | n | | ñ | | | | 918(14) |
| * | 
| 
| 
| 
| 1470 | ½+ | | | ~200 |
| * | 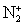
| 
| 
| 
| 1520 | 3∕2- | ý | ~125 |
| * | 
| 
| 
| 
| 1688 | 5∕2+ | | | ~140 |
| * | 
| 
| 
| 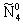
| 2190 | 7∕2- | | | ~250 |
| * | 
| 
| 
| 
| 2220 | 9∕2+ | ø | ~300 |
| * | 
| 
| 
| 
| 
| 
| 
| 
| 1232 | 3∕2+ | ö | 3∕2,1,0 | ~110 |
| * | 
| 
| 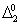
| 
| 
| 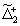
| 
| 
| 1650 | ½- | ý | ~140 |
| * | 
| 
| 
| 
| 
| 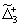
| 
| 
| 1890 | 5∕2+ | | | ~250 |
| * | 
| 
| 
| 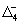
| 
| 
| 
| 
| 1950 | 7∕2+ | ø | ~220 |
| * | L | L̃ | 1115,60(5) | ½+ | 0,0,0 | 2,58(2)×10-10 |
| * | L1 | L̃1 | 1405(5) | ½- | 40(10) |
| * | L2 | L̃2 | 1518(2) | 3∕2- | 16(2) |
| * | L3 | L̃3 | 1820(5) | 5∕2+ | 85 |
| * | L4 | L̃4 | 2100 | 7∕2- | 250 |
| | S+ | | | S̃+ | | | 
| | ö | 1,0,0 | 0,800(6)×10-10 |
| | | S0 | | | S̃0 | | ½+ | | | <1×10-14 |
| | | | S- | | | S̃- | | | | 1,482(17) 10-10 |
| * | S*+ | S*0 | S*- | S̃*+ | S̃*0 | S̃*- | 1383(1) | 3∕2+ | ý | 35(2) |
| * | 
| 
| 
| 
| 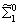
| 
| 1670(10) | 3∕2- | | | ~50 |
| * | 
| 
| 
| 
| 
| 
| 1765(5) | 5∕2- | | | ~120 |
| * | 
| 
| 
| 
| 
| 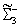
| 2030 | 7∕2+ | ø | ~180 |
| | X0 | | X̃0 | | 
| | ö | ½,—1,0 | 2,96(12) 10-10 |
| | | X- | | X̃- | ½+ | | | 1,65(2) 10-10 |
| * | X*0 | X*- | X̃*0 | X̃*- | 1531,8(3) | 3∕2+ | ý | 9,1(5) |
| * | 
| 
|  X X
| 
| 1820 | ? | ø | ~60 |
| W- | W̃- | 1672,2(4) | 3∕2+ | 0,—2,0 | 1,3(2) 10-10 |
| 
| 
| 2260(10) | ½? | 0,—2∕3,1 | <75? |
| 
| 
| 2450 | ½? | 1,—2∕3,1 | ? |
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
В табл. 1 приведены наиболее хорошо изученные Э. ч. из групп лептонов и адронов и их квантовые числа. В специальную группу выделен фотон. Раздельно даны частицы и античастицы (изменение Р у антибарионов не указано). Абсолютно нейтральные частицы помещены посередине первой колонки. Слева значком * помечены резонансы, для которых вместо т приведена более удобная величина — ширина резонанса  . Члены одного изотопического мультиплета расположены в одной строке, иногда с небольшим смещением (в тех случаях, когда даются характеристики каждого члена мультиплета).
. Члены одного изотопического мультиплета расположены в одной строке, иногда с небольшим смещением (в тех случаях, когда даются характеристики каждого члена мультиплета).
Как следует из табл. 1, лептоны представлены сравнительно небольшим числом частиц: электроном, мюоном, t-лептоном и соответствующими им нейтрино. Массы ve и vm очень малы, но равны ли они в точности нулю, предстоит решить будущим экспериментам; информация о массе vt пока ограничена.
Основную часть Э. ч. составляют адроны. Увеличение числа Э. ч. в 60—70-х гг. происходило исключительно за счёт расширения данной группы. Адроны в своём большинстве представлены резонансами; наблюдается тенденция к росту спина по мере роста массы резонансов, которая хорошо прослеживается на различных группах мезонов и барионов с заданными J и Y и Ch. Следует также отметить, что странные частицы (особенно квазистабильные) несколько тяжелее обычных (нестранных) частиц, а очарованные частицы тяжелее странных.
Классификация элементарных частиц.
Унитарная симметрия. Классификация лептонов пока не представляет проблем, большое же число адронов, известных уже в начале 50-х гг., явилось основанием для поиска закономерностей в распределении масс и квантовых чисел барионов и мезонов, которые могли бы составить основу их классификации. Выделение изотопических мультиплетов адронов было первым шагом на этом пути. С математической точки зрения группировка адронов в изотопические мультиплеты отражает наличие у них симметрии, связанной с группой вращения (см. Группа), более формально, с группой SU (2) — группой унитарных преобразований в комплексном двумерном пространстве. Предполагается, что эти преобразования действуют в некотором специфическом внутреннем пространстве — «изотопическом пространстве», отличном от обычного. Существование изотопического пространства проявляется только в наблюдаемых свойствах симметрии. На математическом языке изотопические мультиплеты суть неприводимые представления группы симметрии SU (2).
Концепция симметрии как фактора, определяющего существование различных групп и семейств Э. ч., в современной теории является доминирующей при классификации адронов и других Э. ч. Предполагается, что внутренние квантовые числа Э. ч., позволяющие выделять те или иные группы частиц, связаны со специальными типами симметрий, возникающими за счёт свободы преобразований в особых «внутренних» пространствах. Отсюда и происходит название «внутренние квантовые числа».
Внимательное рассмотрение показывает, что странные и обычные адроны в совокупности образуют более широкие объединения частиц с близкими свойствами, чем изотопические мультиплеты. Они называются супермультиплетами. Число частиц, входящих в наблюдаемые супермультиплеты, равно 8 и 10. С точки зрения симметрий возникновение супермультиплетов истолковывается как проявление существования у адронов группы симметрии более широкой, чем группа SU (2), а именно: SU (3) — группы унитарных преобразований в трёхмерном комплексном пространстве (М. Гелл-Ман и независимо Ю. Нееман, 1961). Соответствующая симметрия получила назв. унитарной симметрии. Группа SU (3) имеет, в частности, неприводимые представления с числом компонент 8 и 10, отвечающие наблюдаемым супермультиплетам: октету и декуплету. Примерами могут служить следующие группы частиц с одинаковыми значениями J P:

Общими для всех частиц в супермультиплете являются значения двух величин, которые по математической природе близки к изотопическому спину и поэтому часто называются унитарным спином. Для октета значения связанных с этими величинами квантовых чисел равны (1, 1), для декуплета — (3, 0).
Унитарная симметрия менее точная, чем изотопическая симметрия. В соответствии с этим различие в массах частиц, входящих в октеты и декуплеты, довольно значительно. По этой же причине разбиение адронов на супермультиплеты сравнительно просто осуществляется для Э. ч. не очень высоких масс. При больших массах, когда имеется много различных частиц с близкими массами, это разбиение осуществляется менее надёжно. Однако в свойствах Э. ч. имеется много разнообразных проявлений унитарной симметрии.
Включение в систематику Э. ч. очарованных адронов позволяет говорить о сверхсупермультиплетах и о существовании ещё более широкой симметрии, связанной с унитарной группой SU (4). Примеры до конца заполненных сверхсупермультиплетов пока отсутствуют. SU (4)-симметрия нарушена ещё сильнее, чем SU (3)-симметрия, и её проявления выражены слабее.
Обнаружение у адронов свойств симметрии, связанных с унитарными группами, и закономерностей разбиения на мультиплеты, отвечающих строго определённым представлениям указанных групп, явилось основой для вывода о существовании у адронов особых структурных элементов — кварков.
Кварковая модель адронов. Развитие работ по классификации адронов с первых своих шагов сопровождалось попытками выделить среди них частицы более фундаментальные, чем остальные, которые могли бы стать основой для построения всех адронов. Начало этой линии исследования было положено Э. Ферми и Ян Чжэнь-нином (1949), которые предположили, что такими фундаментальными частицами являются нуклон (N) и антинуклон ( ), a p-мезоны есть их связанные состояния (
), a p-мезоны есть их связанные состояния ( ). При дальнейшем развитии этой идеи в число фундаментальных частиц были включены также странные барионы (М. А. Марков, 1955; японский физик С. Саката, 1956; Л. Б. Окунь, 1957). Модели, построенные на этой основе, хорошо описывали мезонные мультиплеты, но не давали правильного описания мультиплетов барионов. Важнейший элемент данных моделей — использование для «построения» адронов небольшого числа фермионов — органически вошёл в модель, которая наиболее успешно решает задачу описания всех адронов, — кварковую модель (австрийский физик Г. Цвейг и независимо М. Гелл-Ман, 1964).
). При дальнейшем развитии этой идеи в число фундаментальных частиц были включены также странные барионы (М. А. Марков, 1955; японский физик С. Саката, 1956; Л. Б. Окунь, 1957). Модели, построенные на этой основе, хорошо описывали мезонные мультиплеты, но не давали правильного описания мультиплетов барионов. Важнейший элемент данных моделей — использование для «построения» адронов небольшого числа фермионов — органически вошёл в модель, которая наиболее успешно решает задачу описания всех адронов, — кварковую модель (австрийский физик Г. Цвейг и независимо М. Гелл-Ман, 1964).
В первоначальном варианте в основу модели было положено предположение, что все известные адроны построены из трёх типов частиц спина 1/2, названных р-, n-, l-кварками, не принадлежащих к числу наблюдавшихся адронов и обладающих весьма необычными свойствами. Название «кварки» заимствовано из романа Дж. Джойса (см. Кварки). Современный вариант модели предполагает существование как минимум четырёх типов кварков. Четвёртый кварк необходим для описания очарованных адронов.
Идея кварков подсказана унитарной симметрией. Математическая структура унитарных групп открывает возможность описания всех представлений группы SU (n) (и, следовательно, всех мультиплетов адронов) на основе самого простого представления группы, содержащего n компонент. В случае группы SU (3) таких компонент три. Необходимо только допустить наличие частиц, связанных с этим простейшим представлением. Эти частицы и есть кварки. Кварковый состав мезонов и барионов был выведен из того факта, что супермультиплеты мезонов содержат, как правило, 8 частиц, а барионов — 8 и 10 частиц. Эта закономерность легко воспроизводится, если предположить, что мезоны составлены из кварка q и антикварка  — символически:
— символически:  , а барионы из трёх кварков — символически: В = (qqq). В силу свойств группы SU (3) 9 мезонов разбиваются на супермультиплеты из 1 и 8 частиц, а 27 барионов — на супермультиплеты, содержащие 1, 10 и дважды по 8 частиц, что и объясняет наблюдаемую выделенность октетов и декуплетов.
, а барионы из трёх кварков — символически: В = (qqq). В силу свойств группы SU (3) 9 мезонов разбиваются на супермультиплеты из 1 и 8 частиц, а 27 барионов — на супермультиплеты, содержащие 1, 10 и дважды по 8 частиц, что и объясняет наблюдаемую выделенность октетов и декуплетов.
Добавление к схеме четвёртого кварка (и, если окажется необходимым, новых дополнительных кварков) осуществляется при сохранении основного предположения кварковой модели о строении адронов:

В = (qqq).
Все экспериментальные данные хорошо соответствуют приведённому кварковому составу адронов. Имеются, видимо, лишь небольшие отклонения от этой структуры, которые не влияют существенным образом на свойства адронов.
Указанная структура адронов и математические свойства кварков, как объектов, связанных с определённым (простейшим) представлением группы SU (4), приводят к след. квантовым числам кварков (табл. 2). Обращают внимание необычные — дробные — значения электрического заряда Q, а также В, S и Y, не встречающиеся ни у одной из наблюдавшихся Э. ч. С индексом a у каждого типа кварка qi (i = 1, 2, 3, 4) связана особая характеристика кварков — «цвет», которой нет у изученных адронов. Индекс a принимает значения 1, 2, 3, т, е. каждый тип кварка qi представлен тремя разновидностями qia (Н. Н. Боголюбов с сотрудниками, 1965; американские физики И. Намбу и М. Хан, 1965; японский физик И. Миямото, 1965). Квантовые числа каждого типа кварка не меняются при изменении «цвета» и поэтому табл. 2 относится к кваркам любого «цвета».
Табл. 2. — Характеристики кварков
| Кварк | Символ | J | I | I3 | S | B | Y | Ch | Q |
| q1a | pa | 1/2 | 1/2 | + 1/2 | 0 | 1/3 | 1/3 | 0 | 2/3 |
| q2a | na | 1/2 | 1/2 | - 1/2 | 0 | 1/3 | 1/3 | 0 | -1/3 |
| q3a | la | 1/2 | 0 | 0 | -1 | 1/3 | -2/3 | 0 | -1/3 |
| q4a | ca | 1/2 | 0 | 0 | - 1/3 | 1/3 | 0 | 1 | 2/3 |
Необходимость введения «цвета» вытекает из требования антисимметрии волновой функции системы кварков, образующих барионы. Кварки, как частицы со спином 1/2, должны подчиняться статистике Ферми — Дирака.
Между тем имеются барионы, составленные из трёх одинаковых кварков, с одинаковой ориентацией спинов: D++(p р р ), W+(l l l ), которые явно симметричны относительно перестановок кварков, если последние не обладают дополнительной степенью свободы. Такой дополнительной степенью свободы и является «цвет». С учётом «цвета» требуемая антисимметрия легко восстанавливается. Уточнённые формулы структурного состава мезонов и барионов выглядят при этом следующим образом:
 ,
,

где eabg — полностью антисимметричный тензор ( ,
,  — нормировочные множители). Важно отметить, что ни мезоны, ни барионы не несут цветовых индексов (лишены цвета) и являются, как иногда говорят, «белыми» частицами.
— нормировочные множители). Важно отметить, что ни мезоны, ни барионы не несут цветовых индексов (лишены цвета) и являются, как иногда говорят, «белыми» частицами.
В табл. 2 не приведены массы кварков. Это связано с тем, что кварки пока выступают лишь как составные части адронов, — в свободном состоянии они не наблюдались, поэтому прямых данных о массах кварков нет. На основании величин масс различных связанных состояний кварков (обычные, странные, очарованные адроны) можно только заключить, что mp ~ mn < ml << mc.
Всё многообразие адронов возникает за счёт различных сочетаний р-, п-, g- и с-кварков, образующих связанные состояния. Обычным адронам соответствуют связанные состояния, построенные только из р- и n-кварков [для мезонов с возможным участием комбинаций  и
и 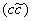 ]. Наличие в связанном состоянии наряду с р- и n-кварками одного g- или с-кварка означает, что соответствующий адрон странный (S = —1) или очарованный (Ch = + 1). В состав бариона может входить два и три g -кварка (соответственно с-кварка), т. е. возможны дважды и трижды странные (очарованные) барионы. Допустимы также сочетания различного числа g- и с-кварков (особенно в барионах), которые соответствуют «гибридным» формам адронов («странно-очарованным»). Очевидно, что чем больше g- или с-кварков содержит адрон, тем он тяжелее. Если сравнивать основные (не возбуждённые) состояния адронов, именно такая картина и наблюдается (см. табл. 1, а также табл. 3 и 5).
]. Наличие в связанном состоянии наряду с р- и n-кварками одного g- или с-кварка означает, что соответствующий адрон странный (S = —1) или очарованный (Ch = + 1). В состав бариона может входить два и три g -кварка (соответственно с-кварка), т. е. возможны дважды и трижды странные (очарованные) барионы. Допустимы также сочетания различного числа g- и с-кварков (особенно в барионах), которые соответствуют «гибридным» формам адронов («странно-очарованным»). Очевидно, что чем больше g- или с-кварков содержит адрон, тем он тяжелее. Если сравнивать основные (не возбуждённые) состояния адронов, именно такая картина и наблюдается (см. табл. 1, а также табл. 3 и 5).
Поскольку спин кварков равен 1/2, приведённая выше кварковая структура адронов имеет своим следствием целочисленный спин у мезонов и полуцелый — у барионов, в полном соответствии с экспериментом. При этом в состояниях, отвечающих орбитальному моменту l = 0, в частности в основных состояниях, значения спина мезонов должны равняться 0 или 1 (для антипараллельной ¯ и параллельной ориентации спинов кварков), а спина барионов — 1/2 или 3/2 (для спиновых конфигураций ¯ и ). С учётом того, что внутренняя чётность системы кварк-антикварк отрицательна, значения JP для мезонов при l = 0 равны 0- и 1-, для барионов — 1/2+ и 3/2+. Именно эти значения JP наблюдаются у адронов, имеющих наименьшую массу при заданных значениях I и Y (см. табл. 1).
Поскольку индексы i, k, l в структурных формулах пробегают значения 1, 2, 3, 4, число мезонов Mik с заданным спином должно быть равно 16. Для барионов Bikl максимально возможное число состояний при заданном спине (64) не реализуется, т. к. в силу принципа Паули при данном полном спине разрешены только такие трёхкварковые состояния, которые обладают вполне определённой симметрией относительно перестановок индексов i, k, 1, а именно: полностью симметричные для спина 3/2 и смешанной симметрии для спина 1/2. Это условие при l = 0 отбирает 20 барионных состояний для спина 3/2 и 20 — для спина 1/2.
Более подробное рассмотрение показывает, что значение кваркового состава и свойств симметрии кварковой системы даёт возможность определить все основные квантовые числа адрона (J, Р, В, Q, I, Y, Ch), за исключением массы; определение массы требует знания динамики взаимодействия кварков и массы кварков, которое пока отсутствует.
Табл. 3. — Кварковый состав мезонов с J P = 0—(¯)
| Частица | Состав | Частица | Состав |
| p+ | pñ | h’ | 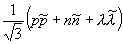
|
| p0 | 
| hc | cc̃ |
| p- | p̃n | F+ | cl̃ |
| h | 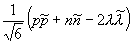
| F- | c̃l |
| K+ | pl̃ | D̃0 | pc̃ |
| K0 | nl̃ | D- | nc̃ |
| K- | p̃l | D0 | p̃c |
| K̃0 | ñl | D+ | ñc |
Табл. 4. — Кварковый состав мезонов с J P = 1—()
| Частица | Состав | Частица | Состав |
| r+ | pñ | j | ll̃ |
| r0 | 
| y | cc̃ |
| r - | p̃n | F*+ | cl̃ |
| w | 
| F*- | c̃l |
| K*+ | pl̃ | D̃*0 | pc̃ |
| K*0 | nl̃ | D*- | nc̃ |
| K*- | p̃l | D*0 | p̃c |
| K̃*0 | ñl | D*+ | ñc |
В качестве иллюстрации в табл. 3 и 4, 5 и 6 приведён вытекающий из описанных представлений кварковый состав мезонов 0- и 1- и барионов 1/2+ и 3/2+ и его соответствие известным частицам (символы наблюдавшихся частиц подчёркнуты). Всюду в таблицах предполагается необходимое суммирование по цветам кварков. Как следует из таблиц, все обычные и странные адроны, которые должны существовать при заданной кварковой структуре, наблюдались экспериментально. Пока нет полных данных для адронов с Ch ¹ 0, однако изученные частицы полностью соответствуют указанной картине.
Правильно передавая специфику адронов с наименьшими массами и спинами при заданных значениях Y и Ch, кварковая модель естественным образом объясняет также общее большое число адронов и преобладание среди них резонансов. Многочисленность адронов — отражение их сложного строения и возможности существования различных возбуждённых состояний кварковых систем. Не исключено, что число таких возбуждённых состояний неограниченно велико. Все возбуждённые состояния кварковых систем неустойчивы относительно быстрых переходов за счёт сильных взаимодействий в нижележащие состояния. Они и образуют основную часть резонансов. Небольшую долю резонансов составляют также кварковые системы с параллельной ориентацией спинов (за исключением W-). Кварковые конфигурации с антипараллельной ориентацией спинов, относящиеся к осн. состояниям, образуют квазистабильные адроны и стабильный протон.
Возбуждения кварковых систем происходят как за счёт изменения вращательного движения кварков (орбитальные возбуждения), так и за счёт изменения их пространств. расположения (радиальные возбуждения). В первом случае рост массы системы сопровождается изменением суммарного спина J и чётности Р системы, во втором случае увеличение массы происходит без изменения JP. Например, мезоны с JP = 2+ являются первым орбитальным возбуждением (l = 1) мезонов с JP = 1-. Соответствие 2+ мезонов и 1- мезонов одинаковых кварковых структур хорошо прослеживается на примере многих пар частиц:

Мезоны r' и y' — примеры радиальных возбуждений r- и y-мезонов соответственно (см. табл. 1).
Орбитальные и радиальные возбуждения порождают последовательности резонансов, отвечающие одной и той же исходной кварковой структуре. Отсутствие надёжных сведений о взаимодействии кварков не позволяет пока производить количественные расчеты спектров возбуждений и делать какие-либо заключения о возможном числе таких возбуждённых состояний.
При формулировке кварковой модели кварки рассматривались как гипотетические структурные элементы, открывающие возможность очень удобного описания адронов. В дальнейшем были проведены эксперименты, которые позволяют говорить о кварках как о реальных материальных образованиях внутри адронов. Первыми были эксперименты по рассеянию электронов нуклонами на очень большие углы. Эти эксперименты (1968), напоминающие классические опыты Резерфорда по рассеянию a-частиц на атомах, выявили наличие внутри нуклона точечных заряженных образований. Сравнение данных этих экспериментов с аналогичными данными по рассеянию нейтрино на нуклонах (1973—75) позволило сделать заключение о средней величине квадрата электрического заряда этих точечных образований. Результат оказался удивительно близким к величине 1/2[(2/3 e)2+(1/3e)2]. Изучение процесса рождения адронов при аннигиляции электрона и позитрона, который предположительно идёт через последовательность процессов: 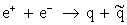 ® адроны, указало на наличие двух групп адронов, генетически связанных с каждым из образующихся кварков, и позволило определить спин кварков. Он оказался равным 1/2. Общее число рожденных в этом процессе адронов свидетельствует также о том, что в промежуточном состоянии возникают кварки трёх разновидностей, т. е. кварки трёхцветны.
® адроны, указало на наличие двух групп адронов, генетически связанных с каждым из образующихся кварков, и позволило определить спин кварков. Он оказался равным 1/2. Общее число рожденных в этом процессе адронов свидетельствует также о том, что в промежуточном состоянии возникают кварки трёх разновидностей, т. е. кварки трёхцветны.
Табл. 5. — Кварковый состав барионов с J P = ½+(¯)
| Частица | Состав | Частица | Состав |
| p | ppn | 
| nnc |
| n | pnn | 
| [pn]c |
| L0 | [pn]l | 
| {pl}c |
| S+ | ppl | 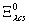
| {nl}c |
| S0 | {pn}l | 
| [pl]c |
| S- | nnl | 
| [nl]c |
| X0 | pll | 
| llc |
| X- | nll | 
| pcc |
| 
| Ppc | 
| ncc |
| 
| {pn}c | 
| lcc |
Табл. 6. — Кварковый состав барионов с J P = 3∕2
| Частица | Состав | Частица | Состав |
| D++ | {ppp} | 
| {ppc} |
| D+ | {ppn} | 
| {pnc} |
| D0 | {pnn} | 
| {nnc} |
| D- | {nnn} | 
| {plc} |
| S*+ | {ppl} | 
| {nlc } |
| S*0 | {pnl} | 
| {llc } |
| S*- | {nnl} | 
| {pcc} |
| X*0 | {pll} | 
| {ncc} |
| X* | {nll} | 
| {lcc} |
| W- | {lll} | 
| {ccc} |
Т. о., квантовые числа кварков, введённые на основании теоретических соображений, получили подтверждение в ряде экспериментов. Кварки постепенно приобретают статус новых Э. ч. Если дальнейшие исследования подтвердят это заключение, то кварки являются серьёзными претендентами на роль истинно Э. ч. для адронной формы материи. До длин ~ 10-15 см кварки выступают как точечные бесструктурные образования. Число известных видов кварков невелико. В дальнейшем оно может, конечно, измениться: нельзя поручиться за то, что при более высоких энергиях не будут обнаружены адроны с новыми квантовыми числами, обязанные своим существованием новым типам кварков. Обнаружение Y -мезонов подтверждает эту точку зрения. Но вполне возможно, что увеличение числа кварков будет небольшим, что общие принципы накладывают ограничения на полное число кварков, хотя эти ограничения пока неизвестны. Бесструктурность кварков также, возможно, отражает лишь достигнутый уровень исследования этих материальных образований. Однако ряд специфических особенностей кварков даёт некоторые основания предполагать, что кварки являются частицами, замыкающими цепь структурных составляющих материи.
От всех других Э. ч. кварки отличаются тем, что в свободном состоянии они пока не наблюдались, хотя имеются свидетельства их существования в связанном состоянии. Одной из причин ненаблюдения кварков может быть их очень большая масса, что препятствует их рождению при энергиях современных ускорителей. Не исключено, однако, что кварки принципиально, в силу специфики их взаимодействия, не могут находиться в свободном состоянии. Существуют доводы теоретического и экспериментального характера в пользу того, что силы, действующие между кварками, не ослабляются с расстоянием. Это означает, что для отделения кварков друг от друга требуется бесконечно большая энергия, или, иначе, возникновение кварков в свободном состоянии невозможно. Невозможность выделить кварки в свободном состоянии делает их совершенно новым типом структурных единиц вещества. Неясно, например, можно ли ставить вопрос о составных частях кварков, если сами кварки нельзя наблюдать в свободном состоянии. Возможно, что в этих условиях части кварков физически вообще не проявляются и поэтому кварки выступают как последняя ступень дробления адронной материи.
Элементарные частицы и квантовая теория поля. Для описания свойств и взаимодействий Э. ч. в современной теории существенное значение имеет понятие физ. поля, которое ставится в соответствие каждой частице. Поле есть специфическая форма материи; оно описывается функцией, задаваемой во всех точках (х) пространства-времени и обладающей определёнными трансформационными свойствами по отношению к преобразованиям группы Лоренца (скаляр, спинор, вектор и т. д.) и групп «внутренних» симметрий (изотопический скаляр, изотопический спинор и т. д.). Электромагнитное поле, обладающее свойствами четырёхмерного вектора Аm(х) (m = 1, 2, 3, 4), — исторически первый пример физического поля. Поля, сопоставляемые с Э. ч., имеют квантовую природу, т. е. их энергия и импульс слагаются из множества отд. порций — квантов, причём энергия Ek и импульс pk кванта связаны соотношением специальной теории относительности: Ek2 = pk2c2 + m2c2. Каждый такой квант и есть Э. ч. с заданной энергией Ek, импульсом pk и массой т. Квантами электромагнитного поля являются фотоны, кванты других полей соответствуют всем остальным известным Э. ч. Поле, т. о., есть физическое отражение существования бесконечной совокупности частиц — квантов. Специальный математический аппарат квантовой теории поля позволяет описать рождение и уничтожение частицы в каждой точке х.
Трансформационные свойства поля определяют все квантовые числа Э. ч. Трансформационные свойства по отношению к преобразованиям пространства-времени (группе Лоренца) задают спин частиц. Так, скаляру соответствует спин 0, спинору — спин 1/2, вектору — спин 1 и т. д. Существование таких квантовых чисел, как L, В, 1, Y, Ch и для кварков и глюонов «цвет», следует из трансформационных свойств полей по отношению к преобразованиям «внутренних пространств» («зарядового пространства», «изотопического пространства», «унитарного пространства» и т. д.). Существование «цвета» у кварков, в частности, связывается с особым «цветным» унитарным пространством. Введение «внутренних пространств» в аппарате теории — пока чисто формальный приём, который, однако, может служить указанием на то, что размерность физического пространства-времени, отражающаяся в свойствах Э. ч., реально больше четырёх — размерности пространства-времени, характерной для всех макроскопических физических процессов. Масса Э. ч. не связана непосредственно с трансформационными свойствами полей; это дополнительная их характеристика.
Для описания процессов, происходящих с Э. ч., необходимо знать, как различные физические поля связаны друг с другом, т. е. знать динамику полей. В современном аппарате квантовой теории поля сведения о динамике полей заключены в особой величине, выражающейся через поля — лагранжиане (точнее, плотности лагранжиана) L. Знание L позволяет в принципе рассчитывать вероятности переходов от одной совокупности частиц к другой под влиянием различных взаимодействий. Эти вероятности даются т. н. матрицей рассеяния (В. Гейзенберг, 1943), выражающейся через L. Лагранжиан L состоит из лагранжиана Lвз, описывающего поведение свободных полей, и лагранжиана взаимодействия Lвз, построенного из полей разных частиц и отражающего возможность их взаимопревращений. Знание Lвз является определяющим для описания процессов с Э. ч.
Вид Lвз однозначно определяется трансформационными свойствами полей относительной группы Лоренца и требованием инвариантности относительно этой группы (релятивистская инвариантность). В течение длительного времени не были, однако, известны критерии для нахождения Lвз (за исключением электромагнитных взаимодействий), а сведения о взаимодействиях Э. ч., полученные из эксперимента, в большинстве случаев не позволяли осуществить надёжный выбор между различными возможностями. В этих условиях широкое распространение получил феноменологический подход к описанию взаимодействий, основанный либо на выборе простейших форм Lвз, ведущих к наблюдаемым процессам, либо на прямом изучении характерных свойств элементов матрицы рассеяния. На этом пути был достигнут значительный успех в описании процессов с Э. ч. для различных выделенных областей энергий. Однако многие параметры теории заимствовались из эксперимента, а сам подход не мог претендовать на универсальность.
В период 50—70-х гг. был достигнут значительный прогресс в понимании структуры Lвз, который позволил существенно уточнить его форму для сильных и слабых взаимодействий. Решающую роль в этом продвижении сыграло выяснение тесной связи между свойствами симметрии взаимодействий Э. ч. и формой Lвз.
Симметрия взаимодействий Э. ч. находит своё отражение в существовании законов сохранения определённых физических величин и, следовательно, в сохранении связанных с ними квантовых чисел Э. ч. (см. Сохранения законы). Точная симметрия, имеющая место для всех классов взаимодействий, отвечает наличию у Э. ч. точных квантовых чисел; приближённая симметрия, характерная лишь для некоторых классов взаимодействий (сильных, электромагнитных), приводит к неточным квантовым числам. Отмечавшееся выше различие классов взаимодействий в отношении сохранения квантовых чисел Э. ч. отражает различия в свойствах их симметрии.
Известная форма Lвзэл. м. для электромагнитных взаимодействий есть следствие существования очевидной симметрии лагранжиана L относительно умножения комплексных полей j заряженных частиц, входящих в него в комбинациях типа j*j (здесь * означает комплексное сопряжение), на множитель eia, где a — произвольное действительное число. Эта симметрия, с одной стороны, порождает закон сохранения электрического заряда, с другой стороны, если требовать выполнения симметрии при условии, что a произвольно зависит от точки х пространства-времени, однозначно приводит к лагранжиану взаимодействия:
Lвзэл. м. = jmэл. м. (x) Am (x) (1)
где jmэл. м. — четырёхмерный электромагнитный ток (см. Электромагнитные взаимодействия). Как выяснилось, этот результат имеет общее значение. Во всех случаях, когда взаимодействия проявляют «внутреннюю» симметрию, т. е. лагранжиан инвариантен относительно преобразований «внутреннего пространства», а у Э. ч. возникают соответствующие квантовые числа, следует требовать, чтобы инвариантность имела место при любой зависимости параметров преобразования от точки х (т. н. локальная калибровочная инвариантность; Ян Чжэнь-нин, американский физик Р. Миллс, 1954). Физически это требование связано с тем, что взаимодействие не может мгновенно передаваться от точки к точке. Указанное условие удовлетворяется, когда среди полей, входящих в лагранжиан, присутствуют векторные поля (аналоги Am (x)), изменяющиеся при преобразованиях «внутренней» симметрии и взаимодействующие с полями частиц вполне определённым образом, а именно:
Lвз = år=1n jmr (x) Vmr (x), (2)
где jmr (x) — токи, составленные из полей частиц, Vmr (x) — векторные поля, называются часто калибровочными полями. Т. о., требование локальности «внутренней» симметрии фиксирует форму Lвз и выделяет векторные поля как универсальные переносчики взаимодействий. Свойства векторных полей и их число «n» определяются свойствами группы «внутренней» симметрии. Если симметрия точная, то масса кванта поля Vmr равна 0. Для приближенной симметрии масса кванта векторного поля отлична от нуля. Вид тока jmr определяется полями частиц с ненулевыми квантовыми числами, связанными с группой «внутренней» симметрии.
На основании изложенных принципов оказалось возможным подойти к вопросу о взаимодействии кварков в нуклоне. Эксперименты по рассеянию нейтрино и антинейтрино на нуклоне показали, что импульс нуклона лишь частично (примерно на 50%) переносится кварками, а остальная его часть переносится другим видом материи, которая не взаимодействует с нейтрино. Предположительно эта часть материи состоит из частиц, которыми обмениваются кварки и за счёт которых они удерживаются в нуклоне. Эти частицы получили название «глюонов» (от английского glue — клей). С изложенной выше точки зрения на взаимодействия эти частицы естественно считать векторными. В современной теории их существование связывается с симметрией, обусловливающей появление «цвета» у кварков. Если эта симметрия точная (цветная SU (3)-симметрия), то глюоны — безмассовые частицы и их число равно восьми (американский физик И. Намбу, 1966). Взаимодействие кварков с глюонами даётся Lвз со структурой (2), где ток jmr составлен из полей кварков. Имеется и основание предполагать, что взаимодействие кварков, обусловленное обменом безмассовыми глюонами, приводит к силам между кварками, не убывающим с расстоянием, но строго это не доказано.
Принципиально знание взаимодействия между кварками могло бы явиться основой для описания взаимодействия всех адронов между собой, т. е. всех сильных взаимодействий. Это направление в физике адронов быстро развивается.
Использование принципа определяющей роли симметрии (в т. ч. приближённой) в формировании структуры взаимодействия позволило также продвинуться в понимании природы лагранжиана слабых взаимодействий. Одновременно была вскрыта глубокая внутренняя связь слабых и электромагнитных взаимодействий. В указанном подходе наличие пар лептонов с одинаковым лептонным зарядом: е-, ve и m-, vm, но различными массами и электрическими зарядами расценивается не как случайное, а как отражающее существование нарушенной симметрии типа изотонической (группа SU (2)). Применение принципа локальности к этой «внутренней» симметрии приводит к характерному лагранжиану (2), в котором одновременно возникают члены, ответственные за электромагнитное и слабое взаимодействия (американский физик С. Вайнберг, 1967; А. Салам, 1968):
Lвз = jmэл. м. + Am + jmсл. з. Wm+ + jmсл. з. Wm- + jmсл. н. Zm0 (3)
Здесь jmсл. з., jmсл. н. — заряженный и нейтральный токи слабых взаимодействий, построенные из полей лептонов, Wm+, Wm-, Zm0 — поля массивных (из-за нарушенности симметрии) векторных частиц, которые в этой схеме являются переносчиками слабых взаимодействий (т. н. промежуточные бозоны), Am — поле фотона. Идея существования заряженного промежуточного бозона была выдвинута давно (Х. Юкава, 1935). Важно, однако, что в данной модели единой теории электрон магнитного и слабого взаимодействий заряженный промежуточный бозон появляется на равной основе с фотоном и нейтральным промежуточным бозоном. Процессы слабых взаимодействий, обусловленные нейтральными токами, были обнаружены в 1973, что подтверждает правильность только что изложенного подхода к формулировке динамики слабых взаимодействий. Возможны и другие варианты написания лагранжиана Lвзсл с большим числом нейтральных и заряженных промежуточных бозонов; для окончательного выбора лагранжиана экспериментальных данных ещё недостаточно.
Экспериментально промежуточные бозоны пока не обнаружены. Из имеющихся данных массы W± и Z0 для модели Вайнберга — Салама оцениваются примерно в 60 и 80 Гэв.
Электромагнитное и слабое взаимодействия кварков можно описать в рамках модели, аналогичной модели Вайнберга — Салама. Рассмотрение на этой основе электромагнитных и слабых взаимодействий адронов даёт хорошее соответствие наблюдаемым данным. Общей проблемой при построении таких моделей является неизвестное пока полное число кварков и лептонов, что не позволяет определить тип исходной симметрии и характер её нарушения. Поэтому очень важны дальнейшие экспериментальные исследования.
Единое происхождение электромагнитных и слабых взаимодействий означает, что в теории исчезает как независимый параметр константа слабых взаимодействий. Единственной константой остаётся электрический заряд е. Подавленность слабых процессов при небольших энергиях объясняется большой массой промежуточных бозонов. При энергиях в системе центра масс, сравнимых с массами промежуточных бозонов, эффекты электромагнитных и слабых взаимодействий должны быть одного порядка. Последние, однако, будут отличаться несохранением ряда квантовых чисел (P, Y, Ch и т. д.).
Имеются попытки рассмотреть на единой основе не только электромагнитные и слабые, но также и сильные взаимодействия. Исходным для таких попыток является предположение об единой природе всех видов взаимодействий Э. ч. (без гравитационного). Наблюдаемые сильные различия между взаимодействиями считаются обусловленными значительным нарушением симметрии. Эти попытки ещё недостаточно разработаны и сталкиваются с серьёзными трудностями, в частности в объяснении различий свойств кварков и лептонов.
Развитие метода получения лагранжиана взаимодействия, основанного на использовании свойств симметрии, явилось важным шагом на пути, ведущем к динамической теории Э. ч. Есть все основания думать, что калибровочные теории поля явятся существенным составным элементом дальнейших теоретических построений.
Некоторые общие проблемы теории элементарных частиц. Новейшее развитие физики Э. ч. явно выделяет из всех Э. ч. группу частиц, которые существенным образом определяют специфику процессов микромира. Эти частицы — возможные кандидаты на роль истинно Э. ч. К их числу принадлежат: частицы со спином 1/2 — лептоны и кварки, а также частицы со спином 1 — глюоны, фотон, массивные промежуточные бозоны, осуществляющие разные виды взаимодействий частиц со спином 1/2. В эту группу скорее всего следует также включить частицу со спином 2 — гравитон; квант гравитационного поля, связывающий все Э. ч. В этой схеме многие вопросы, однако, требуют дальнейшего исследования. Неизвестно, каково полное число лептонов, кварков и различных векторных (с J = 1) частиц и существуют ли физические принципы, определяющие это число. Неясны причины деления частиц со спином 1/2 на 2 различные группы: лептоны и кварки. Неясно происхождение внутренних квантовых чисел лептонов и кварков (L, В, 1, Y, Ch) и такой характеристики кварков и глюонов, как «цвет». С какими степенями свободы связаны внутренние квантовые числа? С обычным четырёхмерным пространством-временем связаны только такие характеристики Э. ч., как J и Р. Какой механизм определяет массы истинно Э. ч.? Чем обусловлено наличие у Э. ч. различных классов взаимодействий с различными свойствами симметрии? Эти и другие вопросы предстоит решить будущей теории Э. ч.
Описание взаимодействий Э. ч., как отмечалось, связано с калибровочными теориями поля. Эти теории имеют развитый математический аппарат, который позволяет производить расчёты процессов с Э. ч. (по крайней мере принципиально) на том же уровне строгости, как и в квантовой электродинамике. Но в настоящем своём виде калибровочные теории поля обладают одним серьёзным недостатком, общим с квантовой электродинамикой, — в них в процессе вычислений появляются бессмысленные бесконечно большие выражения. С помощью специального приёма переопределения наблюдаемых величин (массы и заряда) — перенормировки — удаётся устранить бесконечности из окончательных результатов вычислений. В наиболее хорошо изученной электродинамике это пока не сказывается на согласии предсказаний теории с экспериментом. Однако процедура перенормировки— чисто формальный обход трудности, существующей в аппарате теории, которая на каком-то уровне точности должна сказаться на степени согласия расчётов с измерениями.
Появление бесконечностей в вычислениях связано с тем, что в лагранжианах взаимодействий поля разных частиц отнесены к одной точке х, т. е. предполагается, что частицы точечные, а четырёхмерное пространство-время остаётся плоским вплоть до самых малых расстояний. В действительности указанные предположения, по-видимому, неверны по нескольким причинам: а) истинно Э. ч., вероятнее всего, — материальные объекты конечной протяжённости; б) свойства пространства-времени в малом (в масштабах, определяемых т. н. фундаментальной длиной) скорее всего радикально отличны от его макроскопических свойств; в) на самых малых расстояниях (~10-33 см) сказывается изменение геометрических свойств пространства-времени за счёт гравитации. Возможно, эти причины тесно связаны между собой. Так, именно учёт гравитации наиболее естественно приводит к размерам истинно Э. ч. порядка 10-33 см, а фундамент, длина l0 может быть связана с гравитационной постоянной f:  » 10-33 см. Любая из этих причин должна привести к модификации теории и устранению бесконечностей, хотя практическое выполнение этой модификации может быть весьма сложным.
» 10-33 см. Любая из этих причин должна привести к модификации теории и устранению бесконечностей, хотя практическое выполнение этой модификации может быть весьма сложным.
Очень интересным представляется учёт влияния гравитации на малых расстояниях. Гравитационное взаимодействие может не только устранять расходимости в квантовой теории поля, но и обусловливать само существование первообразующих материи (М. А. Марков, 1966). Если плотность вещества истинно Э. ч. достаточно велика, гравитационное притяжение может явиться тем фактором, который определяет устойчивое существование этих материальных образований. Размеры таких образований должны быть ~10-33 см. В большинстве экспериментов они будут вести себя как точечные объекты, их гравитационное взаимодействие будет ничтожно мало и проявится лишь на самых малых расстояниях, в области, где существенно изменяется геометрия пространства.
Т. о., наметившаяся тенденция к одновременному рассмотрению различных классов взаимодействий Э. ч. скорее всего должна быть логически завершена включением в общую схему гравитационного взаимодействия. Именно на базе одновременного учёта всех видов взаимодействий наиболее вероятно ожидать создания будущей теории Э. ч.
Лит.: Марков М. А., О природе материи, М., 1976; Газиорович С., Физика элементарных частиц, пер. с англ., М., 1969; Коккедэ Я., Теория кварков, пер. с англ., М., 1971; Perkins D. Н., Neutrinos and nucleon structure, «Contemporary Physics», 1975, v. 16, №2; Захаров В. И., Иоффе Б. Л., Окунь Л. Б., Новые элементарные частицы, «Успехи физических наук», 1975, т. 117, в. 2, с. 227; Боголюбов Н. Н., Ширков Д. В., Введение в теорию квантованных полей, 3 изд., М., 1976; Элементарные частицы и компенсирующие поля, пер. с англ., М., 1964; Бернстейн Дж., Спонтанное нарушение симметрии, калибровочные теории, механизм Хиггса и т. п., в кн.: Новости фундаментальной физики, пер. с англ., М., 1977, с 120—240.
А. А. Комар.
 , где
, где  — постоянная Планка, m — масса частицы, с — скорость света) по порядку величин близки к типичным размерам, на которых осуществляется их взаимодействие (например, для p-мезона
— постоянная Планка, m — масса частицы, с — скорость света) по порядку величин близки к типичным размерам, на которых осуществляется их взаимодействие (например, для p-мезона  1,4×10-13 см). Это и приводит к тому, что квантовые закономерности являются определяющими для Э. ч.
1,4×10-13 см). Это и приводит к тому, что квантовые закономерности являются определяющими для Э. ч. ;
;  0,1 mp), однако новейшие данные, видимо, указывают на возможность существования тяжёлых лептонов с такими же массами, как у адронов. Первыми исследованными представителями адронов были протон и нейтрон, лептонов — электрон. Фотон, обладающий только электромагнитными взаимодействиями, не может быть отнесён ни к адронам, ни к лептонам и должен быть выделен в отд. группу. По развиваемым в 70-х гг. представлениям фотон (частица с нулевой массой покоя) входит в одну группу с очень массивными частицами — т. н. промежуточными векторными бозонами, ответственными за слабые взаимодействия и пока на опыте не наблюдавшимися (см. раздел Элементарные частицы и квантовая теория поля).
0,1 mp), однако новейшие данные, видимо, указывают на возможность существования тяжёлых лептонов с такими же массами, как у адронов. Первыми исследованными представителями адронов были протон и нейтрон, лептонов — электрон. Фотон, обладающий только электромагнитными взаимодействиями, не может быть отнесён ни к адронам, ни к лептонам и должен быть выделен в отд. группу. По развиваемым в 70-х гг. представлениям фотон (частица с нулевой массой покоя) входит в одну группу с очень массивными частицами — т. н. промежуточными векторными бозонами, ответственными за слабые взаимодействия и пока на опыте не наблюдавшимися (см. раздел Элементарные частицы и квантовая теория поля). . В этих единицах спин
. В этих единицах спин 







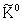
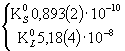




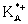




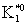





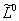



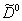









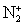










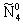














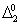


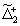







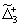





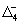









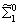












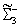









 . Члены одного изотопического мультиплета расположены в одной строке, иногда с небольшим смещением (в тех случаях, когда даются характеристики каждого члена мультиплета).
. Члены одного изотопического мультиплета расположены в одной строке, иногда с небольшим смещением (в тех случаях, когда даются характеристики каждого члена мультиплета).
 ), a
), a  ). При дальнейшем развитии этой идеи в число фундаментальных частиц были включены также странные барионы (М. А.
). При дальнейшем развитии этой идеи в число фундаментальных частиц были включены также странные барионы (М. А.  — символически:
— символически:  , а барионы из трёх кварков — символически: В = (qqq). В силу свойств группы SU (3) 9 мезонов разбиваются на супермультиплеты из 1 и 8 частиц, а 27 барионов — на супермультиплеты, содержащие 1, 10 и дважды по 8 частиц, что и объясняет наблюдаемую выделенность октетов и декуплетов.
, а барионы из трёх кварков — символически: В = (qqq). В силу свойств группы SU (3) 9 мезонов разбиваются на супермультиплеты из 1 и 8 частиц, а 27 барионов — на супермультиплеты, содержащие 1, 10 и дважды по 8 частиц, что и объясняет наблюдаемую выделенность октетов и декуплетов.
 ,
,
 ,
,  — нормировочные множители). Важно отметить, что ни мезоны, ни барионы не несут цветовых индексов (лишены цвета) и являются, как иногда говорят, «белыми» частицами.
— нормировочные множители). Важно отметить, что ни мезоны, ни барионы не несут цветовых индексов (лишены цвета) и являются, как иногда говорят, «белыми» частицами. и
и 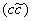 ]. Наличие в связанном состоянии наряду с р- и n-кварками одного
]. Наличие в связанном состоянии наряду с р- и n-кварками одного